选修4-1 第二讲 直线与圆的位置关系 弦切角的性质 课件16张PPT
文档属性
| 名称 | 选修4-1 第二讲 直线与圆的位置关系 弦切角的性质 课件16张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 440.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-20 00:00:00 | ||
图片预览






文档简介
课件16张PPT。2.4弦切角的性质2学习目标1.通过演示对比,探究弦切角的概念2.通过观察、实验、猜想、证明,
明确弦切角定理及简单的应用过程3.知道化归和分类讨论的数学思想3重点弦切角定理及其应用弦切角定理的证明难点4学习过程 2.圆周角∠CAB,让射线AC绕点A旋转,产生无数个圆周角,当AC绕点A旋转至与圆相切时,停止旋转,得∠BAE.(图7-132)思考:
这时∠BAE还是圆周角吗?为什么?
归纳总结出弦切角的特点?1. 什么样的角是圆周角?一、创设情境,以旧探新5学习过程顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角?3.弦切角定义:一、创设情境,以旧探新6学习过程4. 判断下列各图形中的角是不是弦切角,并说明理由:由此发现,弦切角可分为三类:
(1)圆心在角的外部;??
(2)圆心在角的一边上;??
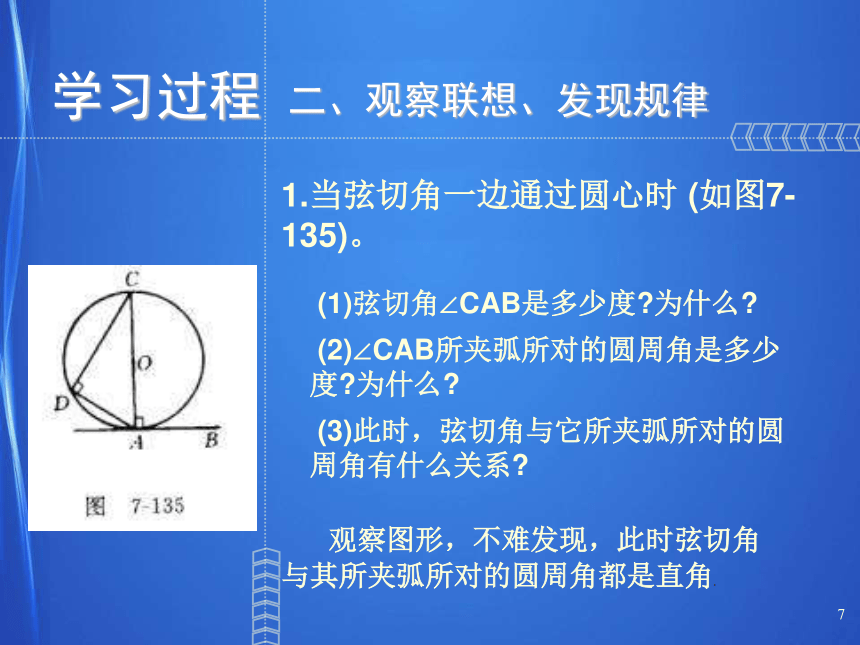
(3)圆心在角的内部.一、创设情境,以旧探新7学习过程1.当弦切角一边通过圆心时 (如图7-135)。
???二、观察联想、发现规律 (1)弦切角∠CAB是多少度?为什么?
(2)∠CAB所夹弧所对的圆周角是多少度?为什么?
(3)此时,弦切角与它所夹弧所对的圆周角有什么关系? 观察图形,不难发现,此时弦切角与其所夹弧所对的圆周角都是直角.8学习过程1.当弦切角一边通过圆心时 (如图7-135)。
???二、观察联想、发现规律 (1)弦切角∠CAB是多少度?为什么?
(2)∠CAB所夹弧所对的圆周角是多少度?为什么?
(3)此时,弦切角与它所夹弧所对的圆周角有什么关系? 观察图形,不难发现,此时弦切角与其所夹弧所对的圆周角都是直角.9学习过程前面证明了特殊情况,下面考虑圆心在弦切角的外部和内部两种情况.?三、类比联想,尝试论证证明:如图7-136(1),圆心O在∠CAB外,作⊙O的直径AQ,连结PQ,
则∠BAC=∠BAQ-∠1=∠APQ-∠2=∠APC.
如图7-136(2),圆心O在∠CAB内,作⊙O的直径AQ,连结PQ,
则∠BAC=∠QAB+∠1=∠QPA+∠2=∠APC.?讨论:怎样将一般情况的证明转化为特殊情况。 ???10学习过程弦切角定理:弦切角等于它所夹的弧对的圆周角.三、类比联想,尝试论证11学习过程例1(课本 )? 如图7-139,已知AB是⊙O的直径,AC是弦,直线CE和⊙O切于点C,AD⊥CE,垂足为D.
求证:AC平分∠BAD.四、巩固知识、初步应用12学习过程例1(课本 )? 如图7-139,已知AB是⊙O的直径,AC是弦,直线CE和⊙O切于点C,AD⊥CE,垂足为D.
求证:AC平分∠BAD.
思路一:
要证∠BAC=∠CAD,可证这两角所在的直角三角形相似,于是连结BC,得Rt△ACB,只需证∠ACD=∠B.(图7-139)四、巩固知识、初步应用13学习过程例1(课本 )? 如图7-139,已知AB是⊙O的直径,AC是弦,直线CE和⊙O切于点C,AD⊥CE,垂足为D.
求证:AC平分∠BAD.
思路二:
连结OC,由切线性质,可得OC∥AD,于是有∠1=∠3,又由于∠1=∠2,可证得结论.(图7-140)四、巩固知识、初步应用课堂小结141.弦切角定理及其应用
2.分类讨论及化归思想的应用.课后作业15 完成导学案达标检测1,2,3.16完毕!再见,谢谢!
明确弦切角定理及简单的应用过程3.知道化归和分类讨论的数学思想3重点弦切角定理及其应用弦切角定理的证明难点4学习过程 2.圆周角∠CAB,让射线AC绕点A旋转,产生无数个圆周角,当AC绕点A旋转至与圆相切时,停止旋转,得∠BAE.(图7-132)思考:
这时∠BAE还是圆周角吗?为什么?
归纳总结出弦切角的特点?1. 什么样的角是圆周角?一、创设情境,以旧探新5学习过程顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角?3.弦切角定义:一、创设情境,以旧探新6学习过程4. 判断下列各图形中的角是不是弦切角,并说明理由:由此发现,弦切角可分为三类:
(1)圆心在角的外部;??
(2)圆心在角的一边上;??
(3)圆心在角的内部.一、创设情境,以旧探新7学习过程1.当弦切角一边通过圆心时 (如图7-135)。
???二、观察联想、发现规律 (1)弦切角∠CAB是多少度?为什么?
(2)∠CAB所夹弧所对的圆周角是多少度?为什么?
(3)此时,弦切角与它所夹弧所对的圆周角有什么关系? 观察图形,不难发现,此时弦切角与其所夹弧所对的圆周角都是直角.8学习过程1.当弦切角一边通过圆心时 (如图7-135)。
???二、观察联想、发现规律 (1)弦切角∠CAB是多少度?为什么?
(2)∠CAB所夹弧所对的圆周角是多少度?为什么?
(3)此时,弦切角与它所夹弧所对的圆周角有什么关系? 观察图形,不难发现,此时弦切角与其所夹弧所对的圆周角都是直角.9学习过程前面证明了特殊情况,下面考虑圆心在弦切角的外部和内部两种情况.?三、类比联想,尝试论证证明:如图7-136(1),圆心O在∠CAB外,作⊙O的直径AQ,连结PQ,
则∠BAC=∠BAQ-∠1=∠APQ-∠2=∠APC.
如图7-136(2),圆心O在∠CAB内,作⊙O的直径AQ,连结PQ,
则∠BAC=∠QAB+∠1=∠QPA+∠2=∠APC.?讨论:怎样将一般情况的证明转化为特殊情况。 ???10学习过程弦切角定理:弦切角等于它所夹的弧对的圆周角.三、类比联想,尝试论证11学习过程例1(课本 )? 如图7-139,已知AB是⊙O的直径,AC是弦,直线CE和⊙O切于点C,AD⊥CE,垂足为D.
求证:AC平分∠BAD.四、巩固知识、初步应用12学习过程例1(课本 )? 如图7-139,已知AB是⊙O的直径,AC是弦,直线CE和⊙O切于点C,AD⊥CE,垂足为D.
求证:AC平分∠BAD.
思路一:
要证∠BAC=∠CAD,可证这两角所在的直角三角形相似,于是连结BC,得Rt△ACB,只需证∠ACD=∠B.(图7-139)四、巩固知识、初步应用13学习过程例1(课本 )? 如图7-139,已知AB是⊙O的直径,AC是弦,直线CE和⊙O切于点C,AD⊥CE,垂足为D.
求证:AC平分∠BAD.
思路二:
连结OC,由切线性质,可得OC∥AD,于是有∠1=∠3,又由于∠1=∠2,可证得结论.(图7-140)四、巩固知识、初步应用课堂小结141.弦切角定理及其应用
2.分类讨论及化归思想的应用.课后作业15 完成导学案达标检测1,2,3.16完毕!再见,谢谢!
