2.2.2 函数的奇偶性课件17张PPT
文档属性
| 名称 | 2.2.2 函数的奇偶性课件17张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 995.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-19 00:00:00 | ||
图片预览






文档简介
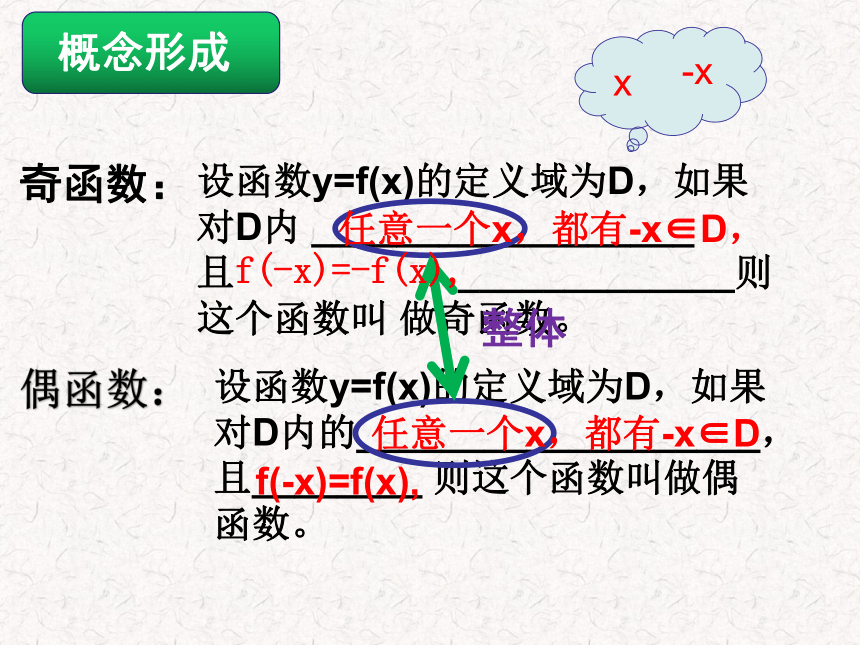
课件17张PPT。课题名称:函数的奇偶性学 科:高中数学年 级:高一版 本:苏教版怎样判断函数的单调性?复习回顾情境引入图示中的图像都有什么特点轴对称建筑陶瓷绘画京剧脸谱庄重大气和谐y=xy=x21y=(x-1)2(1)(2)(3)(4)知识目标:理解奇函数、偶函数的定义及图像特点,会判断函数的奇偶性,能解决与奇偶性相关的问题。能力目标:培养学生分析、归纳的能力,并在奇偶性的探究过程中体会“特殊到一般”和“数形结合”的数学思想方法。情感目标:通过小组讨论的方式增强学生的合作与团队意识。教学目标重点难点函数的奇、偶性和它们的图像特征函数奇偶性的判断设函数y=f(x)的定义域为D,如果对D内 __________________ 且 _____________则这个函数叫 做奇函数。奇函数:偶函数:设函数y=f(x)的定义域为D,如果对D内的___________________, 且________ 则这个函数叫做偶函数。概念形成整体任意一个x,都有-x∈D,
f(-x)=-f(x),任意一个x,都有-x∈Df(-x)=f(x),例题讲解例1:判断下面函数的奇偶性:
(1)f(x)=x+x3+x5①②(2)函数f(x)=x+1的定义域为R,当x∈R,-x∈R因为f(-x)=(-x)+1=-x+1所以函数f(x)=x+1既不是偶函数也不是奇函数。(2)f(x)=x+1 f(-x)≠f(x)且f(-x)≠-f(x)定义域关于原点对称巩固练习(2)f(x)=x2,x∈[1,3](1)f(x)=x2+1定义域不关于原点对称如果一个函数是奇函数,则这个函数的图像是以坐标原点为对称中心的中心对称图形;
反之,如果一个函数的图像是以坐标原点为对称中心的中心对称图形,则这个函数是奇函数●●P(x,f(x))Q(-x,f(-x))P1(-x, )P(x,f(x))P1(-x,-f(x))原点对称由数到形结论1:-f(x)=如果一个函数是偶函数,则这个函数的图像是以y轴为对称轴的轴对称图形;
反之,如果一个函数的图像是以y轴为对称轴的轴对称图形,则这个函数是偶函数●●P(x,f(x))Q(-x,f(-x))y轴对称结论2:y=xy=x21y=(x-1)2(1)(2)(3)(4)不具备奇偶性思考与讨论?1.奇函数的图像一定过(0,0)点吗?2.是不是存在一个函数既是奇函数又 是偶函数?如果0∈D,则f(0)=0y=0应用?抽象函数:利用函数性质画出大体图像数形结合思想-10C拓展提升探究3:1.奇函数与奇函数之间进行加、减、乘、除的四则运算后还是奇函数吗?2.偶函数与偶函数之间进行加、减、乘、除的四则运算后还是偶函数吗?3.奇函数与偶函数之间进行加、减、乘、除的四则运算后,奇偶性能确定吗?加、减后仍为奇函数,乘、除后为偶函数加、减、乘、除后仍为偶函数乘、除后为奇函数当堂小测试1.下列条件,可以说明函数y=f(x)是偶函数的( )
A.在定义域内存在x,使得f(-x)=f(x)
B.在定义域内存在x,使得f(-x)=-f(x)
C.在定义域内任意x,使得f(-x)=-f(x)
D.在定义域内任意x,使得f(-x)=f(x)
2.设函数f(x),g(x)的定义域都是R,且f(x)是奇函数,g(x)是偶函数,则下列结论中正确的是( )
A.f(x)g(x)是偶函数 B.│f(x)│g(x)是奇函数
C. f(x)│g(x)│是奇函数 D. │f(x)g(x)│是奇函数DC课堂小结1.奇函数、偶函数的定义;2.奇函数、偶函数的图像特征;3.函数奇、偶性的性质以及运用。求函数值、解不等式作业:练习A组 1,2
f(-x)=-f(x),任意一个x,都有-x∈Df(-x)=f(x),例题讲解例1:判断下面函数的奇偶性:
(1)f(x)=x+x3+x5①②(2)函数f(x)=x+1的定义域为R,当x∈R,-x∈R因为f(-x)=(-x)+1=-x+1所以函数f(x)=x+1既不是偶函数也不是奇函数。(2)f(x)=x+1 f(-x)≠f(x)且f(-x)≠-f(x)定义域关于原点对称巩固练习(2)f(x)=x2,x∈[1,3](1)f(x)=x2+1定义域不关于原点对称如果一个函数是奇函数,则这个函数的图像是以坐标原点为对称中心的中心对称图形;
反之,如果一个函数的图像是以坐标原点为对称中心的中心对称图形,则这个函数是奇函数●●P(x,f(x))Q(-x,f(-x))P1(-x, )P(x,f(x))P1(-x,-f(x))原点对称由数到形结论1:-f(x)=如果一个函数是偶函数,则这个函数的图像是以y轴为对称轴的轴对称图形;
反之,如果一个函数的图像是以y轴为对称轴的轴对称图形,则这个函数是偶函数●●P(x,f(x))Q(-x,f(-x))y轴对称结论2:y=xy=x21y=(x-1)2(1)(2)(3)(4)不具备奇偶性思考与讨论?1.奇函数的图像一定过(0,0)点吗?2.是不是存在一个函数既是奇函数又 是偶函数?如果0∈D,则f(0)=0y=0应用?抽象函数:利用函数性质画出大体图像数形结合思想-10C拓展提升探究3:1.奇函数与奇函数之间进行加、减、乘、除的四则运算后还是奇函数吗?2.偶函数与偶函数之间进行加、减、乘、除的四则运算后还是偶函数吗?3.奇函数与偶函数之间进行加、减、乘、除的四则运算后,奇偶性能确定吗?加、减后仍为奇函数,乘、除后为偶函数加、减、乘、除后仍为偶函数乘、除后为奇函数当堂小测试1.下列条件,可以说明函数y=f(x)是偶函数的( )
A.在定义域内存在x,使得f(-x)=f(x)
B.在定义域内存在x,使得f(-x)=-f(x)
C.在定义域内任意x,使得f(-x)=-f(x)
D.在定义域内任意x,使得f(-x)=f(x)
2.设函数f(x),g(x)的定义域都是R,且f(x)是奇函数,g(x)是偶函数,则下列结论中正确的是( )
A.f(x)g(x)是偶函数 B.│f(x)│g(x)是奇函数
C. f(x)│g(x)│是奇函数 D. │f(x)g(x)│是奇函数DC课堂小结1.奇函数、偶函数的定义;2.奇函数、偶函数的图像特征;3.函数奇、偶性的性质以及运用。求函数值、解不等式作业:练习A组 1,2
