2.2.2 函数的奇偶性课件18张PPT
文档属性
| 名称 | 2.2.2 函数的奇偶性课件18张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 512.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-19 13:23:41 | ||
图片预览





文档简介
课件18张PPT。2.1.4 函数的奇偶性精美的剪纸一、复习引入1 什么是轴对称图形?
一个图形沿着一条直线折叠,直线两侧的部分完全重合,这样的图形是轴对称图形.这条直线是该图形的对称轴。
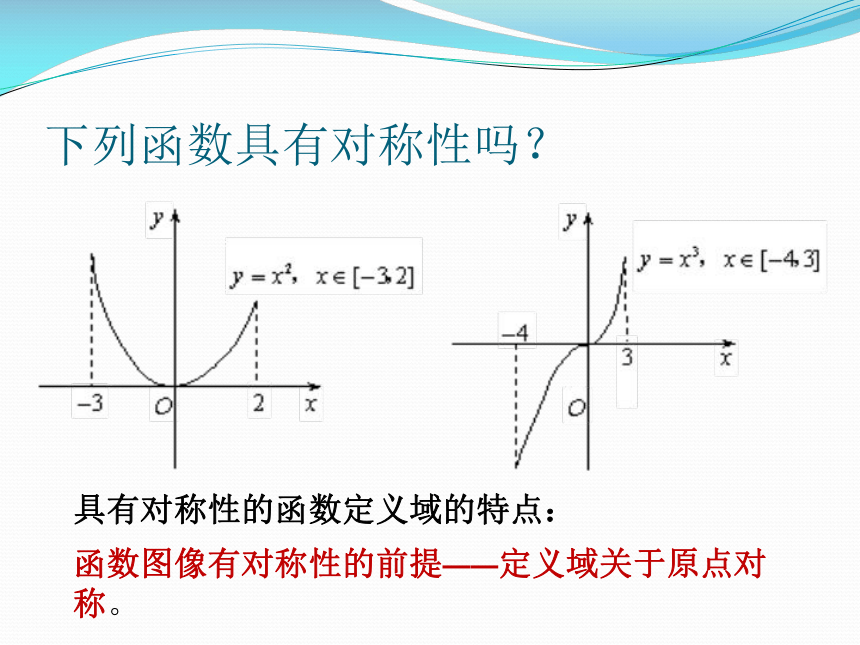
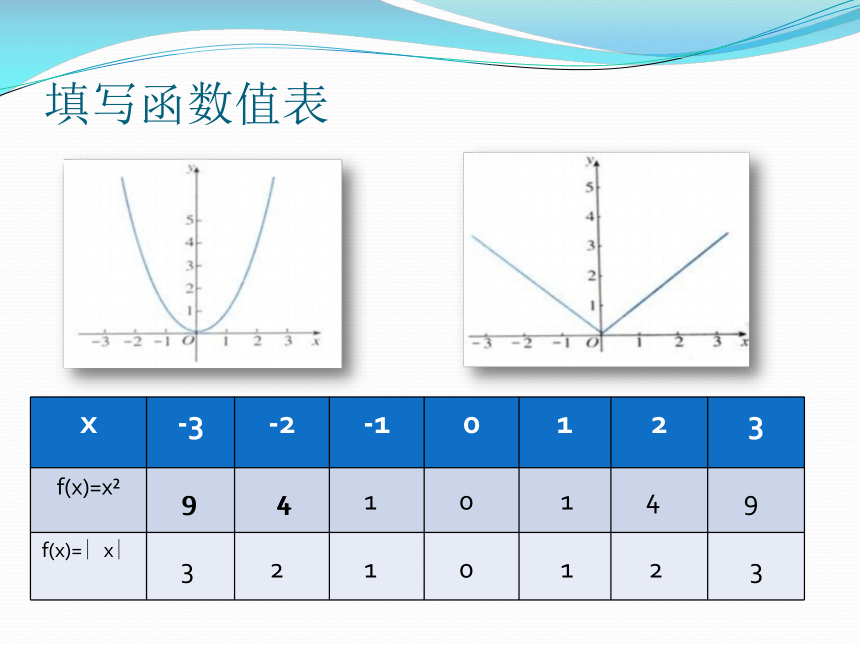
2 什么是中心对称图形观察下面的函数图象:f(x)=x2f(x)=x2f(x)=x2f(x)=x2f(x)=∣x∣⑴⑵⑶⑷下列函数具有对称性吗?具有对称性的函数定义域的特点:函数图像有对称性的前提——定义域关于原点对称。填写函数值表94101493210123944偶函数的定义定义:确定函数f(x)的定义域D, 任取 ,都有
若f(-x)=f(x),则 f(x) 是偶函数。 -3-2-10123-1不存在1奇函数的定义定义:确定函数f(x)的定义域D,任取 都有
若f(-x)=-f(x),则 f(x) 是奇函数 。 判断函数奇偶性的步骤:第一步 确定函数的定义域,并判断其定义域是否关于
原点对称;若不对称,函数既不是奇函数也不 是偶函数,若对称则执行第二步
第二步 确定f(x)和f(-x) 的关系;
第三步 作出判断 :
(1)若f(-x)=f(x),则该函数为偶函数;
(2)若 f(-x)=-f(x),则该函数为奇函数;
(3)若 f(-x)=f(x)且f(-x)=-f(x), 则该函数 既是奇函数又是偶函数;
(4)若 f(-x)≠f(x)且f(-x) ≠ -f(x), 则该函数既不是奇函数也不是偶函数。观察下面的函数图象:f(x)=x2f(x)=x2f(x)=x2f(x)=x2f(x)=∣x∣⑴⑵⑶⑷奇函数和偶函数的图象性质 如果一个函数是奇函数,那么它的图象关于原点中心对称;反之,如果一个函数的图象关于原点中心对称,那么这个函数是奇函数。 如果一个函数是偶函数,那么它的图象关于y轴对称;反之,如果一个函数的图象关于y轴对称,那么这个函数是偶函数。例1.判断下列函数的奇偶性(1) =
⑶ ⑷
⑸
例2 (1)判断函数 的奇偶性;(2)如图是函数 f(x) 图象的一部分,你能根据 f(x)的奇偶性画出它在y轴左边的图象吗?随堂练习 设奇函数f(x)的定义域为[-5,5],若当x∈[0,5]时,f(x)的图象如图,则不等式f(x)<0的解集是______.
小结:1.函数奇偶性的定义.
2.奇函数和偶函数的图象性质.
3.函数奇偶性的判断方法作业:必做题:1.试判断下列函数的奇偶性
??????????
拓展题:2.判断?函数f(x)=a(a是常数)的奇偶性。
3.已知函数????? , 且f(-2) =10 ,求f(2)。 谢 谢
一个图形沿着一条直线折叠,直线两侧的部分完全重合,这样的图形是轴对称图形.这条直线是该图形的对称轴。
2 什么是中心对称图形观察下面的函数图象:f(x)=x2f(x)=x2f(x)=x2f(x)=x2f(x)=∣x∣⑴⑵⑶⑷下列函数具有对称性吗?具有对称性的函数定义域的特点:函数图像有对称性的前提——定义域关于原点对称。填写函数值表94101493210123944偶函数的定义定义:确定函数f(x)的定义域D, 任取 ,都有
若f(-x)=f(x),则 f(x) 是偶函数。 -3-2-10123-1不存在1奇函数的定义定义:确定函数f(x)的定义域D,任取 都有
若f(-x)=-f(x),则 f(x) 是奇函数 。 判断函数奇偶性的步骤:第一步 确定函数的定义域,并判断其定义域是否关于
原点对称;若不对称,函数既不是奇函数也不 是偶函数,若对称则执行第二步
第二步 确定f(x)和f(-x) 的关系;
第三步 作出判断 :
(1)若f(-x)=f(x),则该函数为偶函数;
(2)若 f(-x)=-f(x),则该函数为奇函数;
(3)若 f(-x)=f(x)且f(-x)=-f(x), 则该函数 既是奇函数又是偶函数;
(4)若 f(-x)≠f(x)且f(-x) ≠ -f(x), 则该函数既不是奇函数也不是偶函数。观察下面的函数图象:f(x)=x2f(x)=x2f(x)=x2f(x)=x2f(x)=∣x∣⑴⑵⑶⑷奇函数和偶函数的图象性质 如果一个函数是奇函数,那么它的图象关于原点中心对称;反之,如果一个函数的图象关于原点中心对称,那么这个函数是奇函数。 如果一个函数是偶函数,那么它的图象关于y轴对称;反之,如果一个函数的图象关于y轴对称,那么这个函数是偶函数。例1.判断下列函数的奇偶性(1) =
⑶ ⑷
⑸
例2 (1)判断函数 的奇偶性;(2)如图是函数 f(x) 图象的一部分,你能根据 f(x)的奇偶性画出它在y轴左边的图象吗?随堂练习 设奇函数f(x)的定义域为[-5,5],若当x∈[0,5]时,f(x)的图象如图,则不等式f(x)<0的解集是______.
小结:1.函数奇偶性的定义.
2.奇函数和偶函数的图象性质.
3.函数奇偶性的判断方法作业:必做题:1.试判断下列函数的奇偶性
??????????
拓展题:2.判断?函数f(x)=a(a是常数)的奇偶性。
3.已知函数????? , 且f(-2) =10 ,求f(2)。 谢 谢
