3.2.2 对数函数及其性质课件19张PPT
文档属性
| 名称 | 3.2.2 对数函数及其性质课件19张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 296.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-19 00:00:00 | ||
图片预览





文档简介
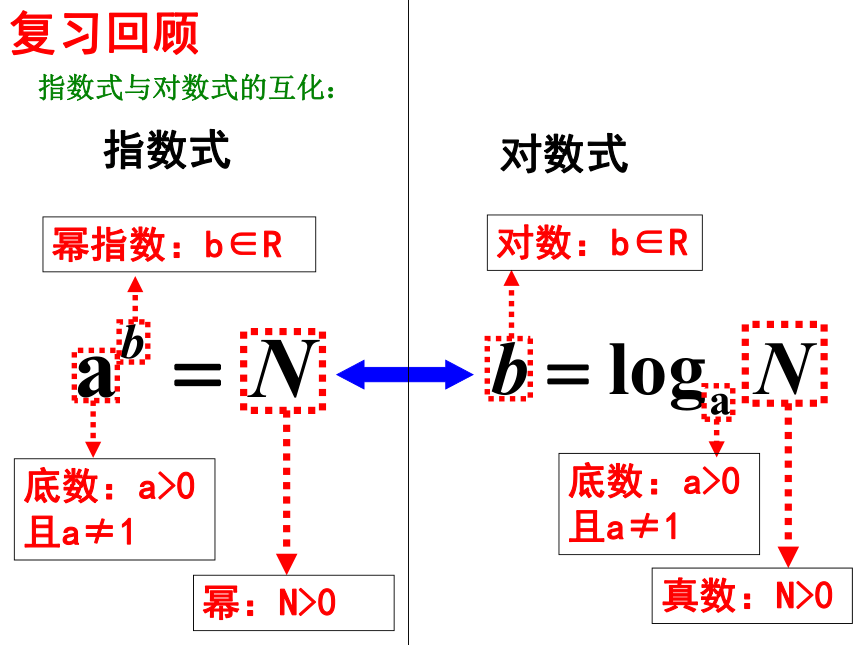
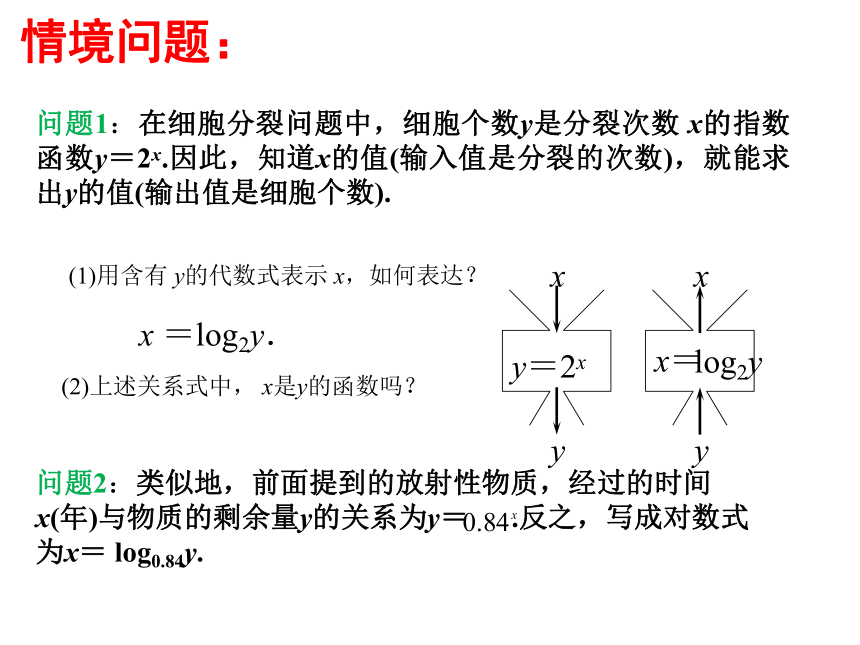
课件19张PPT。3.2.2 对数函数及其性质东台市第一中学 刘娟复习回顾底数:a>0且a≠1幂:N>0真数:N>0底数:a>0且a≠1幂指数:b∈R对数:b∈R 指数式对数式指数式与对数式的互化:情境问题:问题1:在细胞分裂问题中,细胞个数y是分裂次数 x的指数函数y=2x.因此,知道x的值(输入值是分裂的次数),就能求出y的值(输出值是细胞个数).(1)用含有 y的代数式表示 x,如何表达?x =log2y.(2)上述关系式中, x是y的函数吗?xy=2xyxyx=问题2:类似地,前面提到的放射性物质,经过的时间x(年)与物质的剩余量y的关系为y= .反之,写成对数式为x= log0.84y. log2y 上述两个问题中的函数解析式有什么共同特征?探究一:对数形式
自变量在真数位置
底数是常量,探究二:1.定义:一般地,我们把函数 叫做对数函数,其中x是自变量,定义域
为 。练一练:判断下列哪些是对数函数:
1、用描点法画出下列三组函数的图象:
画对数函数:y = loga x (a>0,且a≠ 1) 的图象探究三:和第二组:和第三组:和2、各组中两函数的底数有什么关系,图象有什么关系?
3、在同一坐标系中观察六个函数的图,判断哪些函数是
增函数,哪些函数是减函数,它们的底数有什么共同特征?第一组:思考:从图中你能发现对数函数图像有什么特点?探究:函数 性质当a>1时,y=logax在(0,+∞)为增函数当00当x=1时,总有loga1=0如:log1.059.8
>0比如:log30.9<0即不论底数在a>1或0当x=1时,总有loga1=0比如:log0.39 <0比如:log0.50.8
>0底数和真数的范围相同,则对数大于0;底数和真数的范围不同,则对数小于0;
同正异负数学应用:例1.求下列函数定义域: (1) y=log0.2(4-x)(2) y=loga (a>0且 a≠1)例2.比较大小:(1) log23.4,log23.8;(2)log0.51.8,log0.52.1;(3) log75,log67 ;(4)log3.42;log1.12.数学应用:课堂小结1、本节课我们学习了:
(1) 引入新知---对数函数的定义;
(2) 探究了对数函数的两种图象及其性质;
(3) 比较对数函数的大小---三种类型
(同底不同真、同真不同底、底真都不同);
(4) 思想方法:数形结合;分类讨论方法。
2、作业
作业:课本P87页练习2、3、4、5题
自变量在真数位置
底数是常量,探究二:1.定义:一般地,我们把函数 叫做对数函数,其中x是自变量,定义域
为 。练一练:判断下列哪些是对数函数:
1、用描点法画出下列三组函数的图象:
画对数函数:y = loga x (a>0,且a≠ 1) 的图象探究三:和第二组:和第三组:和2、各组中两函数的底数有什么关系,图象有什么关系?
3、在同一坐标系中观察六个函数的图,判断哪些函数是
增函数,哪些函数是减函数,它们的底数有什么共同特征?第一组:思考:从图中你能发现对数函数图像有什么特点?探究:函数 性质当a>1时,y=logax在(0,+∞)为增函数当0
>0比如:log30.9<0即不论底数在a>1或0
>0底数和真数的范围相同,则对数大于0;底数和真数的范围不同,则对数小于0;
同正异负数学应用:例1.求下列函数定义域: (1) y=log0.2(4-x)(2) y=loga (a>0且 a≠1)例2.比较大小:(1) log23.4,log23.8;(2)log0.51.8,log0.52.1;(3) log75,log67 ;(4)log3.42;log1.12.数学应用:课堂小结1、本节课我们学习了:
(1) 引入新知---对数函数的定义;
(2) 探究了对数函数的两种图象及其性质;
(3) 比较对数函数的大小---三种类型
(同底不同真、同真不同底、底真都不同);
(4) 思想方法:数形结合;分类讨论方法。
2、作业
作业:课本P87页练习2、3、4、5题
