3.3 幂函数 课件 19张PPT
图片预览




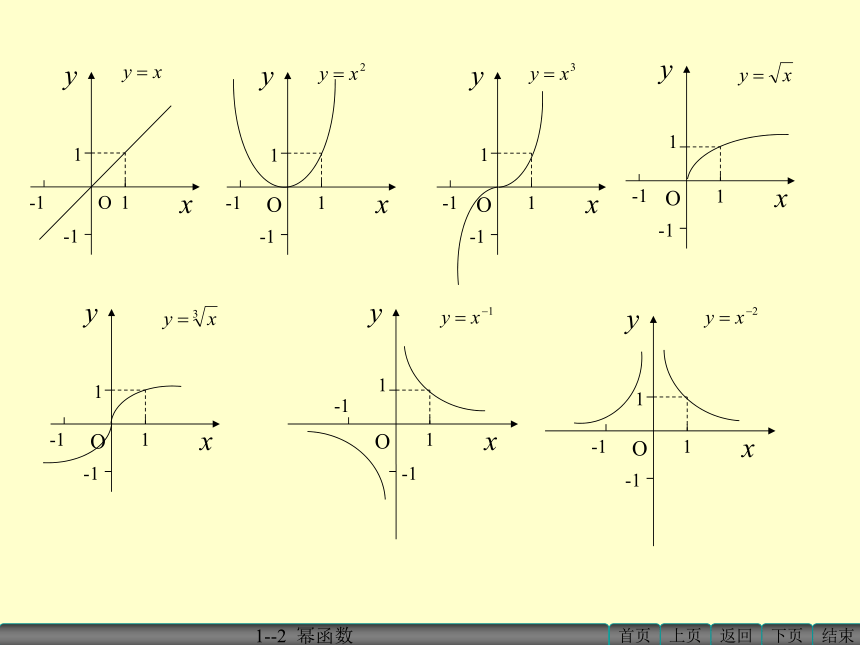

文档简介
课件19张PPT。高中数学 必修一3.3 幂函数情境问题: 指数函数与对数函数是我们刚接触的两类函数模型,我们要将它们与前面所学内容常做比较.我们看下面几个函数问题:1.某人购买了每千克1元的蔬菜x千克,应付y元,这里x与y的关系是什么?5.某人在xs内骑车匀速行进了1km,那么他的速度y(km/s)是多少?2.正方形的边长为x,则它的面积y是多少?3.如果正方体的棱长为x,那么它的体积y是多少?4.如果正方形场地的面积为x,那么它的边长y是多少?思考问题:这些函数有什么共同特征?它们是指数函数吗? 二.幂函数的概念 讨论幂函数的性质: 一般的,我们把形如y=xα(α是常数)的函数叫做幂函数,其中底数x是自变量,指数?是常数。幂函数由于指数α的不同,它们的定义域也不同,性质(有界性、单调性、奇偶性、周期性)也不同。主要通过函数的图像讨论它们的定义域、单调性、奇偶性。定义: 练习:画出下列函数的图像(1). (2).
(3). (4).
(5). (6).
(7).
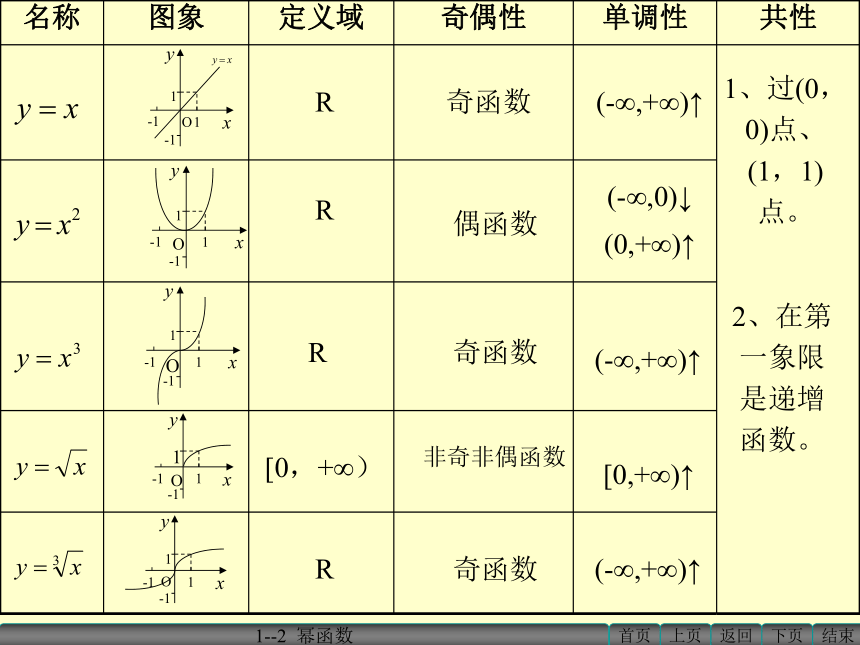
RRR[0,+∞)R奇函数偶函数奇函数非奇非偶函数奇函数(0,+∞)↑(-∞,0)↓(-∞,+∞)↑(-∞,+∞)↑[0,+∞)↑(-∞,+∞)↑2、在第一象限是递增函数。1、过(0,0)点、(1,1)点。奇函数偶函数(-∞,0)∪
(0,+∞)2、在第一象限是递减函数。1、过(1,1)点(-∞,0)∪
(0,+∞)(-∞,0)↓
(0,+∞) ↓(-∞,0) ↑
(0,+∞) ↓数学建构:幂函数的性质:(1)定点: 当?>0时,幂函数图象还通过定点(0,0). 所有幂函数在区间(0,+?)上都有定义,并且都通过点(1,1);(2)单调性: (3)奇偶性: 当?<0时,则在区间(0,+?)上是减函数. 当?>0时,在区间[0,+?)上是增函数,常见的幂函数中,y=x,y=x-1和 y=x3是奇函数; y=x2是偶函数 ;y=x0.5不具有奇偶性. 数学应用:例1 写出下列函数的定义域,并指出它们的奇偶性: (1) (2)y=x-2
(3)y=x2 + x-2 (4) 解:例2:利用幂函数的性质,比较下面各组中两个值的大小例2:利用幂函数的性质,比较下面各组中两个值的大小 解:例2:利用幂函数的性质,比较下面各组中两个值的大小 解:例2:利用幂函数的性质,比较下面各组中两个值的大小解:练习:利用幂函数的性质,比较下面各组中两个值的大小><<=<<练习: 2.下列函数:(1)y=0.2x;(2)y=x0.2;(3)y=x-3;(4)y=3·x-2.其中是幂函数的有 (写出所有幂函数的序号). 3.下列说法:(1)若幂函数的图象过点(-1,1),则此幂函数一定是偶函数;(2)幂函数y=xn(n<0)在其定义域内是减函数;
(3)幂函数y=x0的图象是一条直线;
(4)幂函数y=xn(n>0)在其定义域内是增函数.
其中正确结论的序号是 . (2)(3)(1)(2)(4)4.已知幂函数y=f (x)的图象过点(2, ),则这个函数的解析式为________. 5.函数 的定义域是 .练习:6.当x?(1,+?)时,下列函数:(1)y=x0.5,(2)y=x-2,(3)y=x2,(4)y=x-1中,图象都在直线y=x下方,且是偶函数的是 . 7.幂函数y=x?(??R)的图象一定不经过第 象限. 小结:
对任意的??R,y=x?的图像必将出现在第I象限中;
若y=x?为偶函数,则y=x?的图像必出现在第II象限中;
若y=x?为奇函数,则y=x?的图像必出现在第III象限中;
对任意的??R,y=x?的图像都不会出现在第VI象限中. 练习:(2)4小结:1、学习了幂函数的定义;
2、掌握幂函数在第一象限内的图象特征,并会根据奇偶性完成整个函数的图象。
3、幂函数的性质
4、利用函数的单调性比较几个“同指数不
同底数”的幂的大小.
作业:课本P90-2,4,6.
课后探究:若 , 试求a的取值范围.
(3). (4).
(5). (6).
(7).
RRR[0,+∞)R奇函数偶函数奇函数非奇非偶函数奇函数(0,+∞)↑(-∞,0)↓(-∞,+∞)↑(-∞,+∞)↑[0,+∞)↑(-∞,+∞)↑2、在第一象限是递增函数。1、过(0,0)点、(1,1)点。奇函数偶函数(-∞,0)∪
(0,+∞)2、在第一象限是递减函数。1、过(1,1)点(-∞,0)∪
(0,+∞)(-∞,0)↓
(0,+∞) ↓(-∞,0) ↑
(0,+∞) ↓数学建构:幂函数的性质:(1)定点: 当?>0时,幂函数图象还通过定点(0,0). 所有幂函数在区间(0,+?)上都有定义,并且都通过点(1,1);(2)单调性: (3)奇偶性: 当?<0时,则在区间(0,+?)上是减函数. 当?>0时,在区间[0,+?)上是增函数,常见的幂函数中,y=x,y=x-1和 y=x3是奇函数; y=x2是偶函数 ;y=x0.5不具有奇偶性. 数学应用:例1 写出下列函数的定义域,并指出它们的奇偶性: (1) (2)y=x-2
(3)y=x2 + x-2 (4) 解:例2:利用幂函数的性质,比较下面各组中两个值的大小例2:利用幂函数的性质,比较下面各组中两个值的大小 解:例2:利用幂函数的性质,比较下面各组中两个值的大小 解:例2:利用幂函数的性质,比较下面各组中两个值的大小解:练习:利用幂函数的性质,比较下面各组中两个值的大小><<=<<练习: 2.下列函数:(1)y=0.2x;(2)y=x0.2;(3)y=x-3;(4)y=3·x-2.其中是幂函数的有 (写出所有幂函数的序号). 3.下列说法:(1)若幂函数的图象过点(-1,1),则此幂函数一定是偶函数;(2)幂函数y=xn(n<0)在其定义域内是减函数;
(3)幂函数y=x0的图象是一条直线;
(4)幂函数y=xn(n>0)在其定义域内是增函数.
其中正确结论的序号是 . (2)(3)(1)(2)(4)4.已知幂函数y=f (x)的图象过点(2, ),则这个函数的解析式为________. 5.函数 的定义域是 .练习:6.当x?(1,+?)时,下列函数:(1)y=x0.5,(2)y=x-2,(3)y=x2,(4)y=x-1中,图象都在直线y=x下方,且是偶函数的是 . 7.幂函数y=x?(??R)的图象一定不经过第 象限. 小结:
对任意的??R,y=x?的图像必将出现在第I象限中;
若y=x?为偶函数,则y=x?的图像必出现在第II象限中;
若y=x?为奇函数,则y=x?的图像必出现在第III象限中;
对任意的??R,y=x?的图像都不会出现在第VI象限中. 练习:(2)4小结:1、学习了幂函数的定义;
2、掌握幂函数在第一象限内的图象特征,并会根据奇偶性完成整个函数的图象。
3、幂函数的性质
4、利用函数的单调性比较几个“同指数不
同底数”的幂的大小.
作业:课本P90-2,4,6.
课后探究:若 , 试求a的取值范围.
