第二章 点、直线、平面之间的位置关系(立体几何证明题)单元测试AB卷(解析版)
文档属性
| 名称 | 第二章 点、直线、平面之间的位置关系(立体几何证明题)单元测试AB卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-19 15:23:30 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
A卷
1.边长为2的正方形ABCD所在平面外有一点P,平面ABCD,,E是PC上的一点.
(Ⅰ)求证:AB//平面;
(Ⅱ)求证:平面平面;
(Ⅲ)线段为多长时,平面?
【解析】
(Ⅰ)证明:正方形ABCD中, AB//,又AB平面,平面
所以AB//平面
(Ⅱ)证明:正方形ABCD中,,
平面ABCD,平面ABCD,,
又,所以平面,
平面,平面平面
(Ⅲ)由(Ⅱ)可知,所以只需可证平面,
在中,可求,,,
2.如图,在直三棱柱(侧棱与底面垂直的棱柱)中,点是的中点.
(1)求证: 平面;
(2)若, ,求证: .
试题解析:
证明:(1)连接交于,连接.
在中,因为, 分别为, 的中点,所以,
又因为平面, 平面,所以平面.
(2)直三棱柱,故底面, 平面,所以.
又因为为棱的中点, ,所以,
因为,所以平面,所以,
因为为棱中点,不妨设,所以,
又因为,所以在和中, ,
所以,即,所以,
因为,所以平面,
因为平面,故.
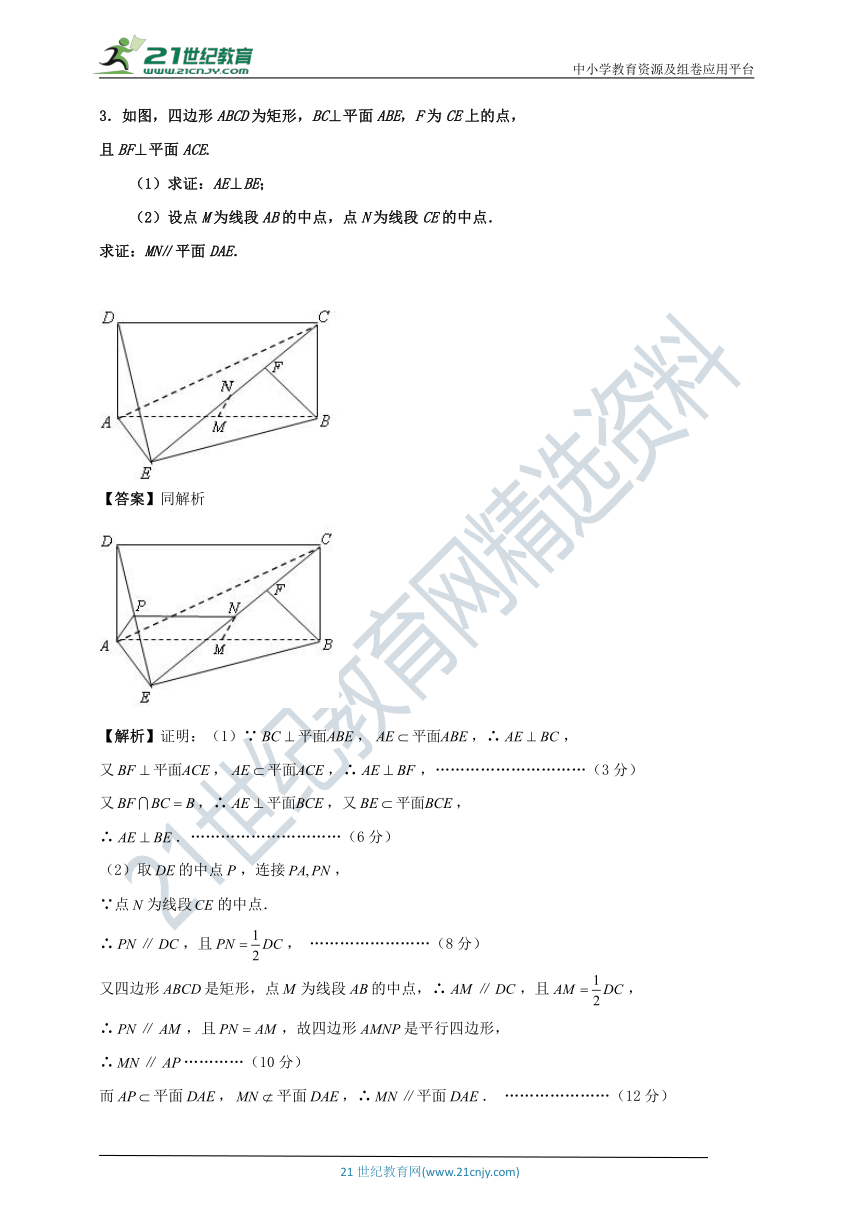
3.如图,四边形ABCD为矩形,BC⊥平面ABE,F为CE上的点,
且BF⊥平面ACE.
(1)求证:AE⊥BE;
(2)设点M为线段AB的中点,点N为线段CE的中点.
求证:MN∥平面DAE.
【答案】同解析
【解析】证明:(1)∵,,∴,
又,,∴,…………………………(3分)
又,∴,又,
∴.…………………………(6分)
(2)取的中点,连接,
∵点为线段的中点.
∴∥,且, ……………………(8分)
又四边形是矩形,点为线段的中点,∴∥,且,
∴∥,且,故四边形是平行四边形,
∴∥…………(10分)
而平面,平面,∴∥平面. …………………(12分)
4.如图,在正三棱柱中,,分别为,的中点.
(1)求证:平面;
(2)求证:平面平面.
试题解析:(1)连交于点, 为中点, ,
为中点, ,
,四边形是平行四边形, 4分
,又平面,平面, 平面. 7分
(2)由(1)知, ,为中点,所以,所以, 9分
又因为底面,而底面,所以,
则由,得,而平面,且,
所以面, 12分
又平面,所以平面平面. 14分
5.如图,在三棱柱ABC-A1B1C1中, CC1⊥底面ABC,AC=BC,M,N分别是CC1,AB的中点.
(1)求证:CN⊥AB1;
(2)求证:CN//平面AB1M.
试题分析:证明:(1)∵三棱柱ABC-A1B1C1中CC1⊥底面ABC,
∴BB1⊥平面ABC, ∴BB1⊥CN.
∵AC=BC,N是AB的中点,∴CN⊥AB.
又∵AB∩BB1=B,∴CN⊥平面AB B1A1,∴CN⊥AB1.
(2)连结A1B交AB1于P.∵三棱柱ABC-A1B1C1,
∴P是A1B的中点.∵M,N分别是CC1,AB的中点,
∴NP // CM,且NP = CM,∴四边形MCNP是平行四边形,
∴CN//MP.∵CN平面AB1M,MP平面AB1M,
∴CN //平面AB1M.
6.在正方体ABCD—A1B1C1D1中,M、N、G分别是A1A,D1C,AD的中点.
求证:(Ⅰ)MN//平面ABCD;(Ⅱ)MN⊥平面B1BG.
【解析】证明:(1)取CD的中点记为E,连NE,AE.
由N,E分别为CD1与CD的中点可得
NE∥D1D且NE=D1D, ………………………………2分
又AM∥D1D且AM=D1D………………………………4分
所以AM∥EN且AM=EN,即四边形AMNE为平行四边形所以MN∥AE,……6分
又AE面ABCD,所以MN∥面ABCD……7分
(2)由AG=DE ,,DA=AB可得与全等 …10分
所以, 又,所以所以, ………………………12分
又,所以, 又MN∥AE,所以MN⊥平面B1BG ……13分
7.
如图所示,凸多面体中,平面,平面,,,,为的中点.
(1)求证:平面;
(2)求证:平面平面.
【解析】证明:(1)作的中点,连接,,∵平面,平面,∴,且平面平面,… 2分∵为三角形的中位线,
∴,,……………… 4分
∴四边形为平行四边形,∴,又平面,平面. ……6分
(2)∵,为的中点
∴,又,∴平面, …… 9分
∵,∴平面,又平面,
∴平面平面. ……… 12分
8.如图,四棱锥的底面是正方形, 平面, 是的中点.
()求证: 平面.
()求证:平面平面.
试题解析:
()证明:连接交于,连接,
∵底面是正方形,
∴是的中点,
又∵是的中点,
∴,
又∵平面, 平面,
∴平面.
()证明:∵平面, 平面,
∴,
∵底面是正方形,
∴,
又,
∴平面,
∵平面,
∴平面平面.
9.如图所示,在直三棱柱中,,平面,D为AC的中点
Ⅰ求证:平面;
Ⅱ求证:平面.
【解析】
(Ⅰ)证明:如图连结,
………………………………………………………………1分
则O为中点,……………………………………………………………………………2分
连OD,∵D为AC中点,
在△中,有OD∥.………………………………………………………………3分
又平面,……………………………………4分
平面,……………………………………5分
∴∥平面.……………………………………6分
(Ⅱ)证明:由,
三棱柱为直三棱柱,
为正方形,
…………………………………………7分
又,
,
,………………………………………8分
又,
又
.……………………………………………………………………9分
又
……………………………………………………………………10分
又
………………………………………………………………11分
……………………………………………………………12分
B卷
10.如图,在四棱锥中,底面是菱形,,且侧面平面,点是棱的中点.
(Ⅰ)求证:平面;
(Ⅱ)求证:;
(Ⅲ)若,求证:平面平面.
【解析】
试题分析:(Ⅰ)由底面是菱形,可得再根据线面平行的性质定理可直接证得平面。(Ⅱ)由面面垂直的性质定理可证得平面,即可证得。(Ⅲ)当时为正三角形,可得,可根据面面的性质定理证得,再根据面面垂直的判定定理可证得面平面。法二时,因为(Ⅱ)中已证,根据线面垂直的判定定理可得平面,从而证得面平面
试题解析:解:(Ⅰ)因为底面是菱形,
所以. 1分
又因为平面, 3分
所以平面. 4分
(Ⅱ)因为,点是棱的中点,
所以. 5分
因为平面平面,平面平面,平面, 7分
所以平面, 8分
因为平面,
所以. 9分
(Ⅲ)因为,点是棱的中点,
所以. 10分
由(Ⅱ)可得, 11分
所以平面, 13分
又因为平面,
所以平面平面. 14分
11.(2013·辽宁高考)如图,AB是圆O的直径,PA垂直圆O所在的平面,C是圆O上的点.
(1)求证:平面PAC⊥平面PBC.
(2)设Q为PA的中点,G为△AOC的重心,求证:QG∥平面PBC.
【解析】(1)由AB是圆的直径,得AC⊥BC;
由PA垂直于圆O所在的平面,得PA⊥平面ABC;又BC?平面ABC,得PA⊥BC.
又PA∩AC=A,PA?平面PAC,AC?平面PAC,
所以BC⊥平面PAC,又BC?平面PBC,所以平面PAC⊥平面PBC.
(2)连接OG并延长交AC于M,
连接QM,QO.由G为△AOC的重心,知M为AC的中点,
由Q为PA的中点,则QM∥PC,
又O为AB中点,得OM∥BC.
因为QM∩MO=M,QM?平面QMO,
MO?平面QMO,BC∩PC=C,BC?平面PBC,PC?平面PBC,
所以平面QMO∥平面PBC.
因为QG?平面QMO,所以QG∥平面PBC.
12.如图:在四棱锥中,底面是菱形,,平面,
点、分别为、的中点,.
(I)证明:平面;
(II)在线段上是否存在一点,使得平面;若存在,求出的长;若不存在,请说明理由。
【解析】解:(Ⅰ)因为为菱形,所以
又,所以,
又为中点,所以
而平面,平面,所以
又,所以平面(6分)
(II)存在
取中点,连结,,,(8分)
因为,分别为、中点,所以且
又在菱形中,,
所以,,即是平行四边形
所以,又平面,平面
所以平面,即在上存在一点,使得平面,(10分)
此时.(12分)
13.如图,在四棱锥中,底面是正方形,侧棱底面,是的中点,求证:
(1)平面 ;
(2).
【详解】
(1)连接AC交BD于O,连接OE,
∵底面ABCD是正方形,∴O为AC中点,
∵在△PAC中,E是PC的中点,
∴OE∥PA,
∵OE?平面EDB,PA?平面EDB,
∴PA∥平面EDB.
(2)∵侧棱PD⊥底面ABCD,AD?底面ABCD,
∴PD⊥AD,
∵底面ABCD是正方形,
∴AD⊥CD,
又PD∩CD=D,
∴AD⊥平面PCD.
∴AD⊥PC.
14.如图,在空间几何体ABCDFE中,底面是边长为2的正方形,,,.
(1)求证:AC//平面DEF;
(2)已知,若在平面上存在点,使得平面,试确定点的位置.
试题解析:
(1)连BD交AC于O,取DE中点K,连结OK、KF
∵AC、BD是正方形的对角线
∴O为BD中点,∴,∴四边形AOKF为平行四边形,∴
又∵平面DEF,平面DEF
∴AC//平面DEF
(2)在△DAF中,,,,所以
又因为,,平面ABCD
∴平面.
以为原点,、、分别为、、轴建立空间直角坐标系(如图).
则,,,,,
设,因为,,
又,
所以,
∵∴
解得即.所以是线段上靠近的三等分点.
15.在正方体中,E,F分别是CD,A1D1中点
(1)求证:AB1⊥BF;
(2)求证:AE⊥BF;
(3)棱CC1上是否存在点P,使BF⊥平面AEP,若存在,
确定点P的位置;若不存在,说明理由
【解析】解:(1)证明:连结A1B,CD1 ∵AB1⊥A1B, AB1⊥BC,A1B∩BC=B ∴AB1⊥平面A1BCD1 , 又BF平面A1BCD1 ,所以AB1⊥BF
(2) 证明:取AD中点M,连结FM,BM
∵ABCD为正方形,E,M分别为所在棱的中点,
∴AE⊥BM,又∵FM⊥AE,BM∩FM=M,
∴AE⊥平面BFM, 又BF平面BFM,∴AE⊥BF
(3) 存在,P是CC1的中点,则易证PE∥AB1,故A,B1,E,P四点共面
证明:由(1)(2)知AB1⊥BF,AE⊥BF,AB1∩AE=A,∴BF⊥平面AEB1,
即BF⊥平面AEP
16.如图, 在直三棱柱中,,,,,点是的中点.
(1)求证:;
(2)求证://平面.
试题解析:(Ⅰ)∵三棱柱底面三边长
∴
又∵底面
∴.?
∵
∴平面
∴
(Ⅱ)设与的交点为, 连结
∵是的中点,是的中点,
∴∥????????????????????????
∵平面,平面
∴∥平面.?
17.如图,在三棱锥中, 分别为的中点.
(1)求证: 平面;
(2)若平面平面,且, ,
求证:平面平面.
【答案】(1)证明:连结, 、分别为、的中点,
. ……………………2分
又平面, 平面, EF∥平面PAB. …………5分
(2), 为的中点, ………6分
又平面平面
面……………………8分
……………………9分
又因为为的中点,
……………10分
面……………………11分
又面 面面
18.如图,边长为4的正方形与矩形所在平面互相垂直,分别为的中点,.
(1)求证:平面;
(2)求证:平面;
(3)在线段上是否存在一点,使得?若存在,求出的长;若不存在,请说明理由.
试题解析:(I)因为为正方形,所以。
因为平面,,,所以.
(Ⅱ)连结
因为是的中点,且为矩形,所以也是的中点。因为是的中点,所以∥,因为,所以MN∥平面CDFE。
(Ⅲ)过点作交线段于点,则点即为所求。因为ABCD为正方形,所以∥。因为,所以,因为,所以。因为,且,所以,因为,所以。因为与相似,所以,因为,所以。
考点:线线平行、线面平行、线线垂直、线面垂直。
第18题图
D
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
