1.1正弦定理(一)课件(17张PPT)
文档属性
| 名称 | 1.1正弦定理(一)课件(17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 480.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-20 21:53:52 | ||
图片预览



文档简介
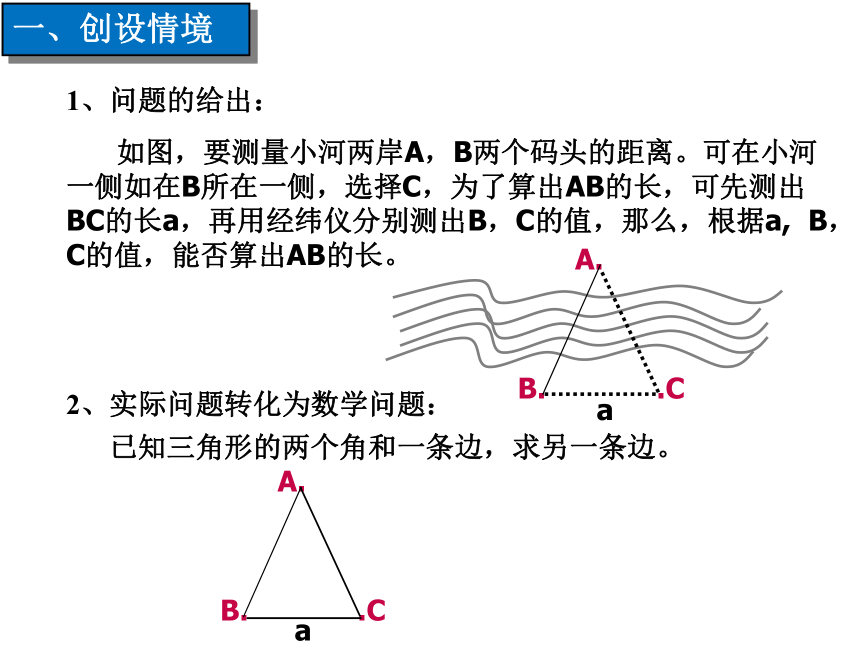
课件17张PPT。北师大版高中数学必修五第二章第一节 正弦定理(一)一、创设情境1、问题的给出:2、实际问题转化为数学问题:
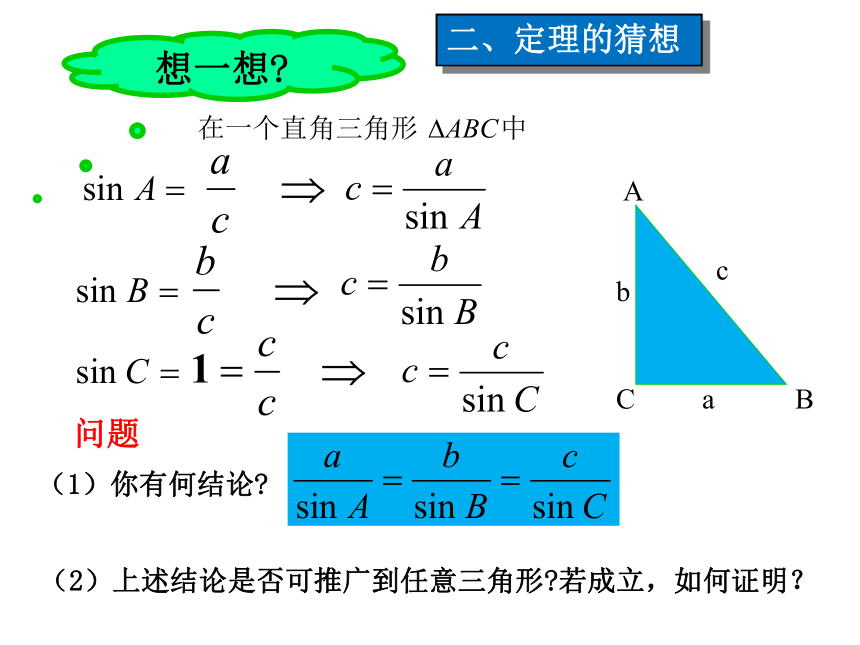
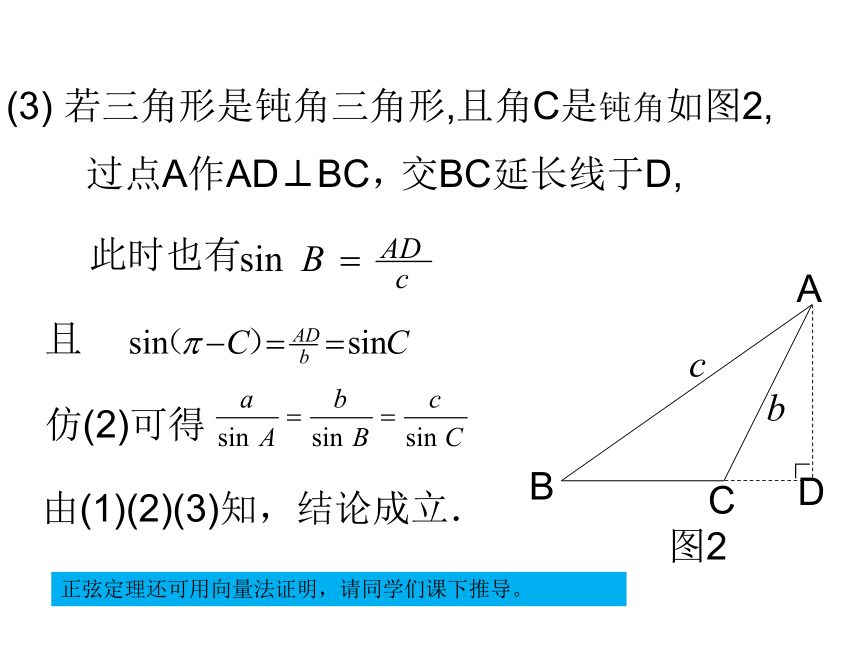
如图,要测量小河两岸A,B两个码头的距离。可在小河一侧如在B所在一侧,选择C,为了算出AB的长,可先测出BC的长a,再用经纬仪分别测出B,C的值,那么,根据a, B,C的值,能否算出AB的长。.CaACBcba想一想?问题 (2)上述结论是否可推广到任意三角形?若成立,如何证明?(1)你有何结论?二、定理的猜想(1) 若直角三角形,已证得结论成立.所以AD=csinB=bsinC, 即同理可得过点A作AD⊥BC于D,此时有 (2)若三角形是锐角三角形, 如图1,三、定理的证明由(1)(2)(3)知,结论成立.且仿(2)可得(3) 若三角形是钝角三角形,且角C是钝角如图2, 此时也有交BC延长线于D,过点A作AD⊥BC,正弦定理还可用向量法证明,请同学们课下推导。(1)文字叙述正弦定理:在一个三角形中,各边和它所对角 的正弦的比相等.(2)结构特点(3)方程的思想正弦定理实际上是已知其中三个,求另一个.和谐美、对称美.正弦定理:如图:若测得a=48.1m,B=43 ° ,
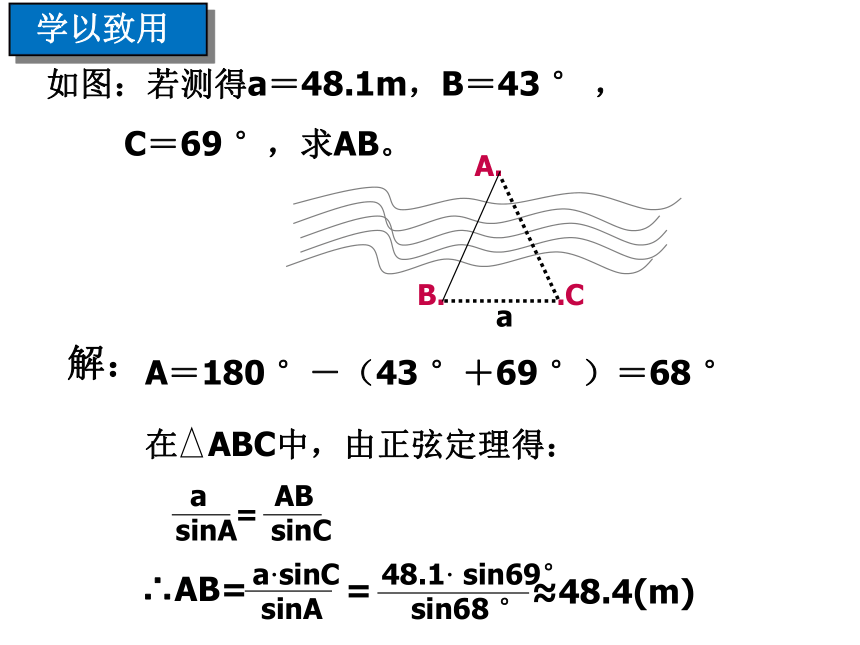
C=69 °,求AB。解:A=180 °-(43 °+69 °)=68 °≈48.4(m) 学以致用试一试解:∵正弦定理应用一:
已知两角和任意一边,求其余两边和一角例⒉在△ABC中,已知a=2,b= ,A=45°,
求B和c。变式1:在△ABC中,已知a=4,b= ,A=45°,
求B和c。变式2:在△ABC中,已知a= ,b= ,A=45°,
求B和c。
正弦定理应用二:
已知两边和其中一边对角,求另一边的对角,进
而可求其它的边和角。(要注意可能有两解)
点拨:已知两角和任意一边,求其余两边和一角,
此时的解是唯一的.课堂练习点拨:已知两边和其中一边的对角解三角形时,通常要用到三角形内角定理和定理或大边对大角定理等三角形有关性质.
二种 —— 平面几何法 向量法定理应用方法 课时小结二个 —— 已知两角和一边(只有一解)
已知两边和其中一边的对角
(有一解,两解,无解) 思考题: 作业
如图,要测量小河两岸A,B两个码头的距离。可在小河一侧如在B所在一侧,选择C,为了算出AB的长,可先测出BC的长a,再用经纬仪分别测出B,C的值,那么,根据a, B,C的值,能否算出AB的长。.CaACBcba想一想?问题 (2)上述结论是否可推广到任意三角形?若成立,如何证明?(1)你有何结论?二、定理的猜想(1) 若直角三角形,已证得结论成立.所以AD=csinB=bsinC, 即同理可得过点A作AD⊥BC于D,此时有 (2)若三角形是锐角三角形, 如图1,三、定理的证明由(1)(2)(3)知,结论成立.且仿(2)可得(3) 若三角形是钝角三角形,且角C是钝角如图2, 此时也有交BC延长线于D,过点A作AD⊥BC,正弦定理还可用向量法证明,请同学们课下推导。(1)文字叙述正弦定理:在一个三角形中,各边和它所对角 的正弦的比相等.(2)结构特点(3)方程的思想正弦定理实际上是已知其中三个,求另一个.和谐美、对称美.正弦定理:如图:若测得a=48.1m,B=43 ° ,
C=69 °,求AB。解:A=180 °-(43 °+69 °)=68 °≈48.4(m) 学以致用试一试解:∵正弦定理应用一:
已知两角和任意一边,求其余两边和一角例⒉在△ABC中,已知a=2,b= ,A=45°,
求B和c。变式1:在△ABC中,已知a=4,b= ,A=45°,
求B和c。变式2:在△ABC中,已知a= ,b= ,A=45°,
求B和c。
正弦定理应用二:
已知两边和其中一边对角,求另一边的对角,进
而可求其它的边和角。(要注意可能有两解)
点拨:已知两角和任意一边,求其余两边和一角,
此时的解是唯一的.课堂练习点拨:已知两边和其中一边的对角解三角形时,通常要用到三角形内角定理和定理或大边对大角定理等三角形有关性质.
二种 —— 平面几何法 向量法定理应用方法 课时小结二个 —— 已知两角和一边(只有一解)
已知两边和其中一边的对角
(有一解,两解,无解) 思考题: 作业
