1.1正弦定理 课件(31张PPT)
文档属性
| 名称 | 1.1正弦定理 课件(31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 834.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-20 00:00:00 | ||
图片预览











文档简介
课件31张PPT。2.1.2 余弦定理必修5第二章《解三角形》 正弦定理的外在形式是什么?其数学意义如何?
复习回顾1.正弦定理 在一个三角形中,各边和它所对角的正弦之比相等,且等于外接圆直径.2.用正弦定理能解决的问题(1) 已知三角形的两角和任一边解三角形
(2) 已知两边和其中一边的对角解三角形
(注意解的情况)
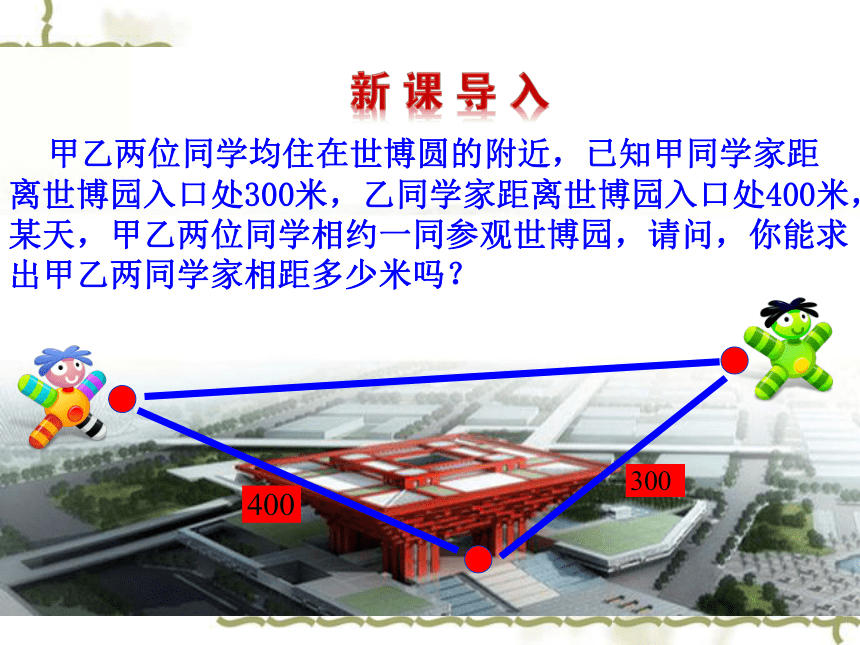
(3) 判断三角形的形状. 甲乙两位同学均住在世博圆的附近,已知甲同学家距离世博园入口处300米,乙同学家距离世博园入口处400米,某天,甲乙两位同学相约一同参观世博园,请问,你能求出甲乙两同学家相距多少米吗? 已知三角形的两边及其夹角,解三角形。能解这个三角形吗? 根据三角形全等的判定方法,这个三角形是大小、形状完全确定的三角形. 从量化的角度来看,如何从已知的两边和它们的夹角求三角形的另一边和两个角? 这就是我们这节课要讲的内容.实际问题数学化1.掌握余弦定理的两种表示形式及证明余弦定理的向量方法.(重点)2.会运用余弦定理解决两类基本的解三角形问题.(难点)问题 已知两边和它们的夹角,求三角形的另一边 用正弦定理试求,发现因A、B均未知,所以较难求边c. 由于涉及边长问题,从而可以考虑用向量来研究这个问题.即:如图,在△ABC中,设BC=a, AC=b, AB=c.已知a, b和C,求边c. 思考1:在△ABC中,已知边a,b和角C,从向量的角度考虑,可以求出什么?c思考2:c边的长即为 ,向量 与 , 有什么关系?思考3:如何将 转化为c与a,b,C的关系?利用向量的数量积可求长度 和夹角。探究(一):余弦定理的推导思考4:根据上述推导可得,
此式对任意三角形都成立吗?根据上述推导同理可得:思考5:如图所示建立直角坐标系,点A,B的坐标分别是什么?
根据两点间的距离公式可得什么结论? A(bcosC,bsinC)B(a,0)c思考6:通过类比,a2,b2分别等于什么?思考7:上述三个等式称为余弦定理.如何用文字语言描述余弦定理? 三角形中任何一边的平方,等于其他两边的平方和,减去这两边与其夹角的余弦的积的两倍. 探究(二):余弦定理的变式思考1:在△ABC中,若已知边a,b和角C,如何求边c和角A,B? 当已知两边及其夹角解三角形时,先用余弦定理求出第三边,其余角的求解有两种思路:一是利用余弦定理的推论来求;二是利用正弦定理来求。但用正弦定理求解时,要注意角的取舍,而用余弦定理求解就不存在角的取舍问题,故用余弦定理求解较好。思考2:已知三角形的三边a,b,c,求三内角A,B,C,其计算公式如何?思考3:上述三个公式是余弦定理的推论,如何通过三边的大小关系判断∠A是锐角、直角还是钝角?勾股定理A为钝角;A为锐角.根据余弦定理的推论:推论:提炼:设a是最长的边,则△ABC是钝角三角形△ABC是锐角三角形△ABC是直角三角形与思考3对比思考4:若已知边a,b和角A,能直接用余弦定理求边c吗? 可以注意:边长 只取 ,因为 。正值三角形边长为正思考5:结合正弦定理,可作什么变形?同理可得其它两种变形:剖析余弦定理(1)本质:揭示的是三角形三条边与某一角的关系, 从
方程的角度看,已知三个量,可以求出第四个量;(2)余弦定理是勾股定理的推广,勾股定理是余弦定理 的特例;(3)主要解决两类三角形问题:已知三边求三角;
已知两边及它们的夹角,求第三边;(4)余弦定理的优美形式和简洁特征:给定一个三角形任意一个角都可以通过已知三边求出;三个式子的结构式是完全一致的。思考6:勾股定理指出了直角三角形中三边平方之间的关系,余弦定理则指出了一般三角形中三边平方之间的关系,如何看这两个定理之间的关系?由此可知余弦定理是勾股定理的推广,勾股定理是余弦定理的特例. 思考7.在△ABC中,若a2=b2+c2,a2>b2+c2,a2b2+c2,a2若a2>b2+c2,则△ABC是钝角三角形;
若a2 思维突破:已知两边及其夹角,可直接使用
余弦定理求解.
课堂互动讲练解:由余弦定理,得反思与感悟:当已知两边及其夹角解三角形时,先用余弦定理求出第三边,其余角的求解有两种思路:一是利用余弦定理的推论来求;二是利用正弦定理来求。但用正弦定理求解时,要注意角的取舍,而用余弦定理求解就不存在角的取舍问题,故用余弦定理求解较好。【变式与拓展】
D注意:本题也可用正弦定理直接求解。题型 2已知三边(或三边的关系)解三角形
三角形的最大内角.
思维突破:已知三边,可直接使用余弦定理求解.
解:显然,角 C 最大. ∴C=120°.反思与感悟:当已知三边(或三边的关系)解三角形时, 若已知三角形三边的比例关系时,常根据比例的性质引入参数 k ,从而转化为已知三边求解。 若已知三角形三边时,可用余弦定理的推论与三角形内角和定理求出三个角。 【变式与拓展】
2.在△ABC 中,sinA∶sinB∶sinC=2∶3∶4,则△ABC是( )
A.锐角三角形
C.直角三角形
B.钝角三角形
D.不能判断3.已知三角形三边之比为 5∶7∶8,则最大角与最小角的和为_______.120°B2. 余弦定理的应用范围: 1.余弦定理是任何三角形边角之间存在的共同规律,勾股定理是余弦定理的特例.①已知三边求三角;
②已知两边及它们的夹角,求第三边.课后作业P51 练习:1,2,3
P53 习题2--1:2,3,5,6被人揭下面具是一种失败,自己揭下面具却是一种胜利.
——雨果再见
复习回顾1.正弦定理 在一个三角形中,各边和它所对角的正弦之比相等,且等于外接圆直径.2.用正弦定理能解决的问题(1) 已知三角形的两角和任一边解三角形
(2) 已知两边和其中一边的对角解三角形
(注意解的情况)
(3) 判断三角形的形状. 甲乙两位同学均住在世博圆的附近,已知甲同学家距离世博园入口处300米,乙同学家距离世博园入口处400米,某天,甲乙两位同学相约一同参观世博园,请问,你能求出甲乙两同学家相距多少米吗? 已知三角形的两边及其夹角,解三角形。能解这个三角形吗? 根据三角形全等的判定方法,这个三角形是大小、形状完全确定的三角形. 从量化的角度来看,如何从已知的两边和它们的夹角求三角形的另一边和两个角? 这就是我们这节课要讲的内容.实际问题数学化1.掌握余弦定理的两种表示形式及证明余弦定理的向量方法.(重点)2.会运用余弦定理解决两类基本的解三角形问题.(难点)问题 已知两边和它们的夹角,求三角形的另一边 用正弦定理试求,发现因A、B均未知,所以较难求边c. 由于涉及边长问题,从而可以考虑用向量来研究这个问题.即:如图,在△ABC中,设BC=a, AC=b, AB=c.已知a, b和C,求边c. 思考1:在△ABC中,已知边a,b和角C,从向量的角度考虑,可以求出什么?c思考2:c边的长即为 ,向量 与 , 有什么关系?思考3:如何将 转化为c与a,b,C的关系?利用向量的数量积可求长度 和夹角。探究(一):余弦定理的推导思考4:根据上述推导可得,
此式对任意三角形都成立吗?根据上述推导同理可得:思考5:如图所示建立直角坐标系,点A,B的坐标分别是什么?
根据两点间的距离公式可得什么结论? A(bcosC,bsinC)B(a,0)c思考6:通过类比,a2,b2分别等于什么?思考7:上述三个等式称为余弦定理.如何用文字语言描述余弦定理? 三角形中任何一边的平方,等于其他两边的平方和,减去这两边与其夹角的余弦的积的两倍. 探究(二):余弦定理的变式思考1:在△ABC中,若已知边a,b和角C,如何求边c和角A,B? 当已知两边及其夹角解三角形时,先用余弦定理求出第三边,其余角的求解有两种思路:一是利用余弦定理的推论来求;二是利用正弦定理来求。但用正弦定理求解时,要注意角的取舍,而用余弦定理求解就不存在角的取舍问题,故用余弦定理求解较好。思考2:已知三角形的三边a,b,c,求三内角A,B,C,其计算公式如何?思考3:上述三个公式是余弦定理的推论,如何通过三边的大小关系判断∠A是锐角、直角还是钝角?勾股定理A为钝角;A为锐角.根据余弦定理的推论:推论:提炼:设a是最长的边,则△ABC是钝角三角形△ABC是锐角三角形△ABC是直角三角形与思考3对比思考4:若已知边a,b和角A,能直接用余弦定理求边c吗? 可以注意:边长 只取 ,因为 。正值三角形边长为正思考5:结合正弦定理,可作什么变形?同理可得其它两种变形:剖析余弦定理(1)本质:揭示的是三角形三条边与某一角的关系, 从
方程的角度看,已知三个量,可以求出第四个量;(2)余弦定理是勾股定理的推广,勾股定理是余弦定理 的特例;(3)主要解决两类三角形问题:已知三边求三角;
已知两边及它们的夹角,求第三边;(4)余弦定理的优美形式和简洁特征:给定一个三角形任意一个角都可以通过已知三边求出;三个式子的结构式是完全一致的。思考6:勾股定理指出了直角三角形中三边平方之间的关系,余弦定理则指出了一般三角形中三边平方之间的关系,如何看这两个定理之间的关系?由此可知余弦定理是勾股定理的推广,勾股定理是余弦定理的特例. 思考7.在△ABC中,若a2=b2+c2,a2>b2+c2,a2
若a2
余弦定理求解.
课堂互动讲练解:由余弦定理,得反思与感悟:当已知两边及其夹角解三角形时,先用余弦定理求出第三边,其余角的求解有两种思路:一是利用余弦定理的推论来求;二是利用正弦定理来求。但用正弦定理求解时,要注意角的取舍,而用余弦定理求解就不存在角的取舍问题,故用余弦定理求解较好。【变式与拓展】
D注意:本题也可用正弦定理直接求解。题型 2已知三边(或三边的关系)解三角形
三角形的最大内角.
思维突破:已知三边,可直接使用余弦定理求解.
解:显然,角 C 最大. ∴C=120°.反思与感悟:当已知三边(或三边的关系)解三角形时, 若已知三角形三边的比例关系时,常根据比例的性质引入参数 k ,从而转化为已知三边求解。 若已知三角形三边时,可用余弦定理的推论与三角形内角和定理求出三个角。 【变式与拓展】
2.在△ABC 中,sinA∶sinB∶sinC=2∶3∶4,则△ABC是( )
A.锐角三角形
C.直角三角形
B.钝角三角形
D.不能判断3.已知三角形三边之比为 5∶7∶8,则最大角与最小角的和为_______.120°B2. 余弦定理的应用范围: 1.余弦定理是任何三角形边角之间存在的共同规律,勾股定理是余弦定理的特例.①已知三边求三角;
②已知两边及它们的夹角,求第三边.课后作业P51 练习:1,2,3
P53 习题2--1:2,3,5,6被人揭下面具是一种失败,自己揭下面具却是一种胜利.
——雨果再见
