1.2余弦定理 课件(26张PPT)
文档属性
| 名称 | 1.2余弦定理 课件(26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 497.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-20 00:00:00 | ||
图片预览



文档简介
课件26张PPT。1余弦定理2直角三角形中的边角关系:1、角的关系:A+B+C=180°
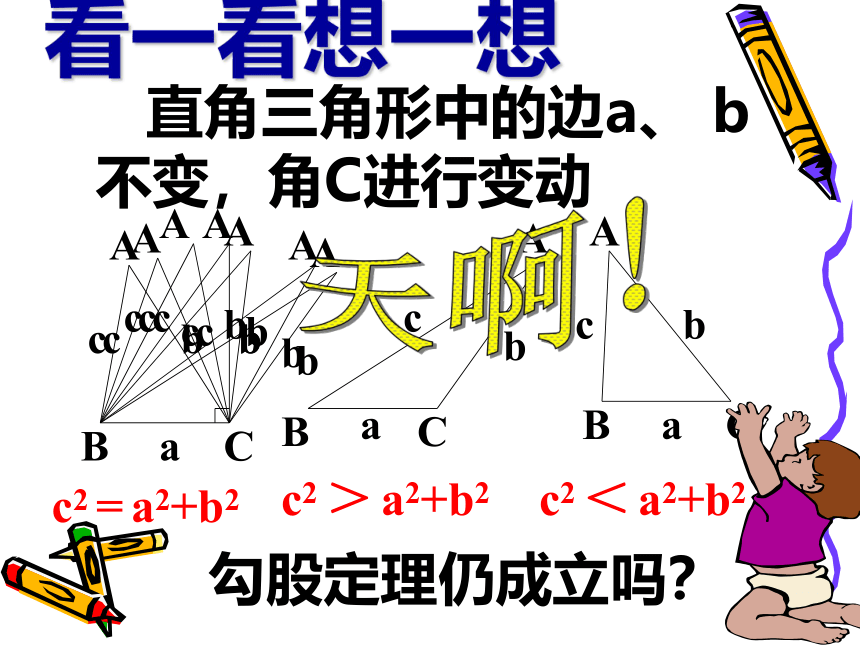
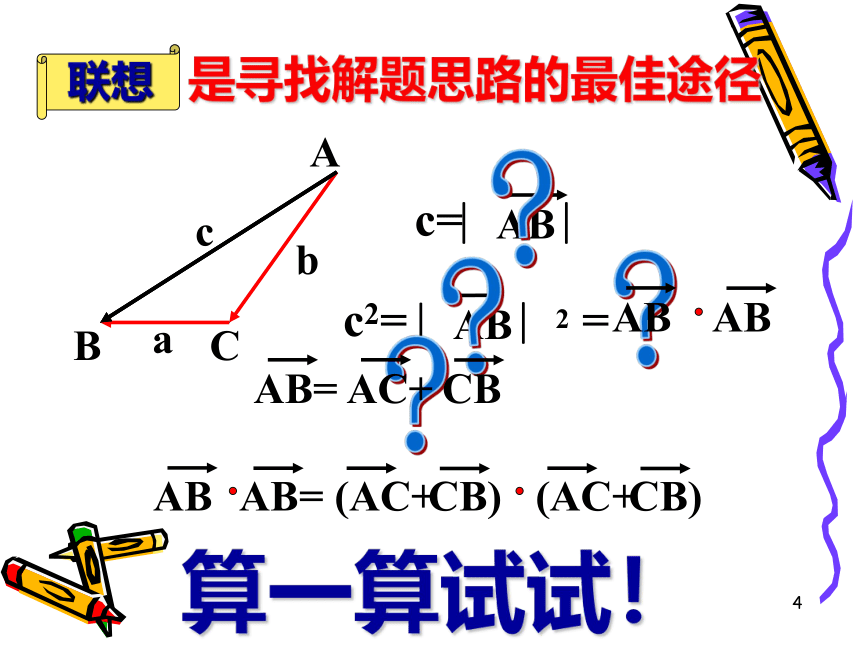
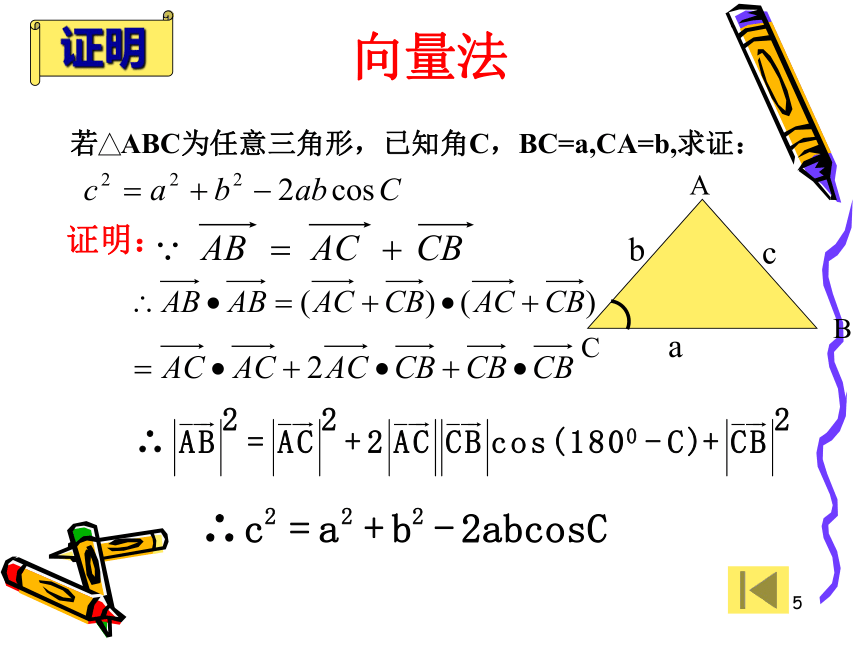
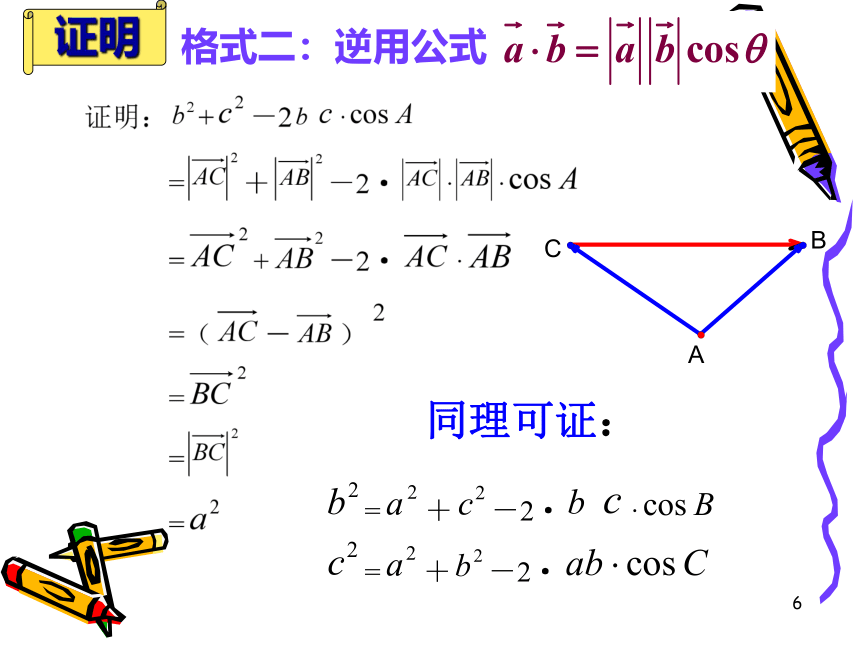
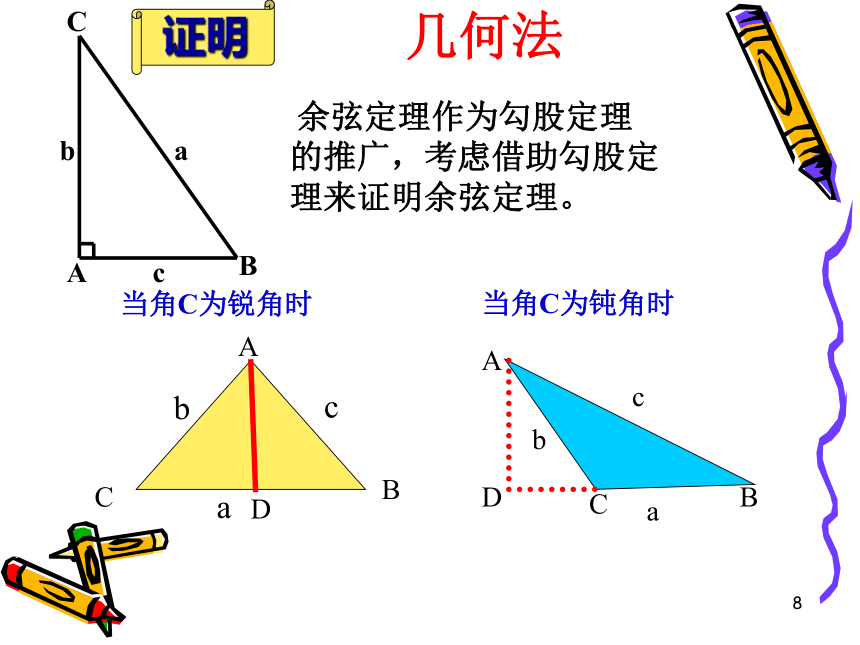
A+B=C=90 °2、边的关系: a2+b2=c23、边角关系:复习3CBAabcc2 > a2+b2c2 < a2+b2看一看想一想 直角三角形中的边a、 b不变,角C进行变动勾股定理仍成立吗?天啊!c2 = a2+b24是寻找解题思路的最佳途径 c=? c2==???算一算试试!联想5证明:向量法证明6同理可证: 格式二:逆用公式证明7证明:以CB所在的直线为x轴,过C点垂直于CB的直线为y轴,建立如图所示的坐标系,则A、B、C三点的坐标分别为:解析法证明8当角C为锐角时几何法
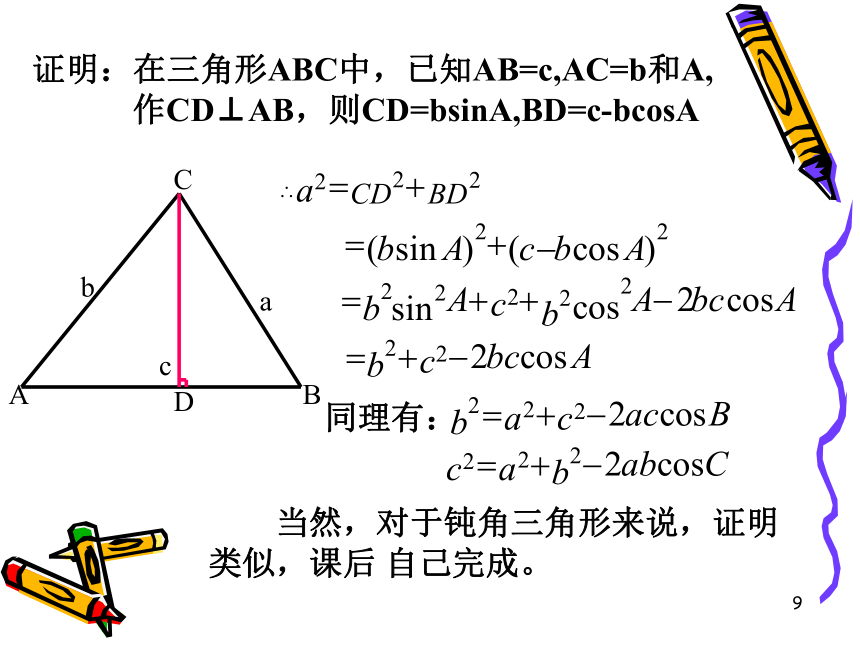
当角C为钝角时 余弦定理作为勾股定理的推广,考虑借助勾股定理来证明余弦定理。证明9证明:在三角形ABC中,已知AB=c,AC=b和A, 作CD⊥AB,则CD=bsinA,BD=c-bcosA同理有: 当然,对于钝角三角形来说,证明类似,课后 自己完成。10余弦定理 a2=b2+c2-2bc·cosA
b2=c2+a2-2ca·cosB
c2=a2+b2-2ab·cosC你能用文字说明吗? 三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。归纳11变一变乐在其中 a2=b2+c2-2bc·cosA
b2=c2+a2-2ca·cosB
c2=a2+b2-2ab·cosC变形归纳12想一想: 余弦定理在直角三角 形中是否仍然成立? a2+b2=c213问题1:勾股定理与余弦定理有何关系?勾股定理是余弦定理的特例,余弦定理是勾股定理的推广.问题2:公式的结构特征怎样?(1)轮换对称,简洁优美;剖 析 定 理(2)每个等式中有同一个三角形中的四个元素,知三求一.(方程思想)
剖析14思考: 已知两边及一边的对角时,我们知道可用正弦定理来解三角形,想一想能不能用余弦定理来解这个三角形?
如:已知b=4,c= ,C=60°求边a.15(3)已知a、b、c(三边),可以求什么?剖 析 定 理剖析16剖 析 定 理(4)能否把式子 转化为角的关系式?分析:剖析17(1)已知三边求三个角;问题3:余弦定理在解三角形中的作用是什么?(2)已知两边和它们的夹角,求第三边和其他两个角.剖 析 定 理剖析18 例、已知△ABC中AB=2、AC=3、A= ,求BC 的长。解:由余弦定理可知
BC2=AB2+AC2-2AB×AC·cosA
=4+9-2×2×3×
=7
∴BC=典 例 剖 析19练一练: 1、已知△ABC的三边为 、2、1,求它的最大内角。变一变:若已知三边的比是 :2:1,又怎么求?20再练:在 中,已知(a+b+c)(a+b-c)=3ab
求角C 21例2:(1)在三角形ABC中,已知
a=7,b=10,c=6,判定三角形ABC的形状分析:三角形ABC的形状是由大边b所对的大角B决定的。(2)在三角形ABC中,已知a=7,b=10,c=6,求三角形ABC的面积分析:三角形的面积公式 S= absinC = bcsinA= acsinB, 只需先求出cosC(cosA或cosB),然后求出 sinC(sinA或 sinB)代入面积公式即可。22练一练:在三角形ABC中,已知 sinA=2sinBcosC,
试判断三角形ABC的形状。232.余弦定理3.由余弦定理知1.证明定理:课堂小结向量法、解析法、几何法24(1)已知三边求三个角;(2)已知两边和它们的夹角,求第三边和其他两个角.5.余弦定理的作用4.余弦定理适用于任何三角形25(3)边角互化;(4)已知两边及其一边的对角,求第三边.5.余弦定理的作用续(5)判断三角形的形状,
求三角形的面积26欢迎指导!
A+B=C=90 °2、边的关系: a2+b2=c23、边角关系:复习3CBAabcc2 > a2+b2c2 < a2+b2看一看想一想 直角三角形中的边a、 b不变,角C进行变动勾股定理仍成立吗?天啊!c2 = a2+b24是寻找解题思路的最佳途径 c=? c2==???算一算试试!联想5证明:向量法证明6同理可证: 格式二:逆用公式证明7证明:以CB所在的直线为x轴,过C点垂直于CB的直线为y轴,建立如图所示的坐标系,则A、B、C三点的坐标分别为:解析法证明8当角C为锐角时几何法
当角C为钝角时 余弦定理作为勾股定理的推广,考虑借助勾股定理来证明余弦定理。证明9证明:在三角形ABC中,已知AB=c,AC=b和A, 作CD⊥AB,则CD=bsinA,BD=c-bcosA同理有: 当然,对于钝角三角形来说,证明类似,课后 自己完成。10余弦定理 a2=b2+c2-2bc·cosA
b2=c2+a2-2ca·cosB
c2=a2+b2-2ab·cosC你能用文字说明吗? 三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。归纳11变一变乐在其中 a2=b2+c2-2bc·cosA
b2=c2+a2-2ca·cosB
c2=a2+b2-2ab·cosC变形归纳12想一想: 余弦定理在直角三角 形中是否仍然成立? a2+b2=c213问题1:勾股定理与余弦定理有何关系?勾股定理是余弦定理的特例,余弦定理是勾股定理的推广.问题2:公式的结构特征怎样?(1)轮换对称,简洁优美;剖 析 定 理(2)每个等式中有同一个三角形中的四个元素,知三求一.(方程思想)
剖析14思考: 已知两边及一边的对角时,我们知道可用正弦定理来解三角形,想一想能不能用余弦定理来解这个三角形?
如:已知b=4,c= ,C=60°求边a.15(3)已知a、b、c(三边),可以求什么?剖 析 定 理剖析16剖 析 定 理(4)能否把式子 转化为角的关系式?分析:剖析17(1)已知三边求三个角;问题3:余弦定理在解三角形中的作用是什么?(2)已知两边和它们的夹角,求第三边和其他两个角.剖 析 定 理剖析18 例、已知△ABC中AB=2、AC=3、A= ,求BC 的长。解:由余弦定理可知
BC2=AB2+AC2-2AB×AC·cosA
=4+9-2×2×3×
=7
∴BC=典 例 剖 析19练一练: 1、已知△ABC的三边为 、2、1,求它的最大内角。变一变:若已知三边的比是 :2:1,又怎么求?20再练:在 中,已知(a+b+c)(a+b-c)=3ab
求角C 21例2:(1)在三角形ABC中,已知
a=7,b=10,c=6,判定三角形ABC的形状分析:三角形ABC的形状是由大边b所对的大角B决定的。(2)在三角形ABC中,已知a=7,b=10,c=6,求三角形ABC的面积分析:三角形的面积公式 S= absinC = bcsinA= acsinB, 只需先求出cosC(cosA或cosB),然后求出 sinC(sinA或 sinB)代入面积公式即可。22练一练:在三角形ABC中,已知 sinA=2sinBcosC,
试判断三角形ABC的形状。232.余弦定理3.由余弦定理知1.证明定理:课堂小结向量法、解析法、几何法24(1)已知三边求三个角;(2)已知两边和它们的夹角,求第三边和其他两个角.5.余弦定理的作用4.余弦定理适用于任何三角形25(3)边角互化;(4)已知两边及其一边的对角,求第三边.5.余弦定理的作用续(5)判断三角形的形状,
求三角形的面积26欢迎指导!
