2.2等差数列的前n项和 课件(21张PPT)
文档属性
| 名称 | 2.2等差数列的前n项和 课件(21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-20 00:00:00 | ||
图片预览








文档简介
课件21张PPT。
§2 等差数列
§2.2 等差数列的前n项和高斯
德国数学家,物理学家,天文学家,大地测量学家,
犹太民族。他是一位多产的数学家,光以“高斯”名字
命名的科研成果就有110项,有“数学王子”之称。
高斯与阿基米德、牛顿并列为历史上最伟大的数学家。
阿基米德
“力学之父”,他有一句与杠杆原理有关的名言是:“给我一个支点,我就能撬起整个地球。”
阿基米德原理:物体在液体中所受浮力等于它所排开液体的重量。
牛顿 苹果 万有引力 牛顿三大定律
他们都是百科全书式科学家。
多产数学家
数学王子
高斯“数学王子”高斯是德国数学家.在高斯10岁时,老师出了一道数学题:1到100的所有整数的和为多少?
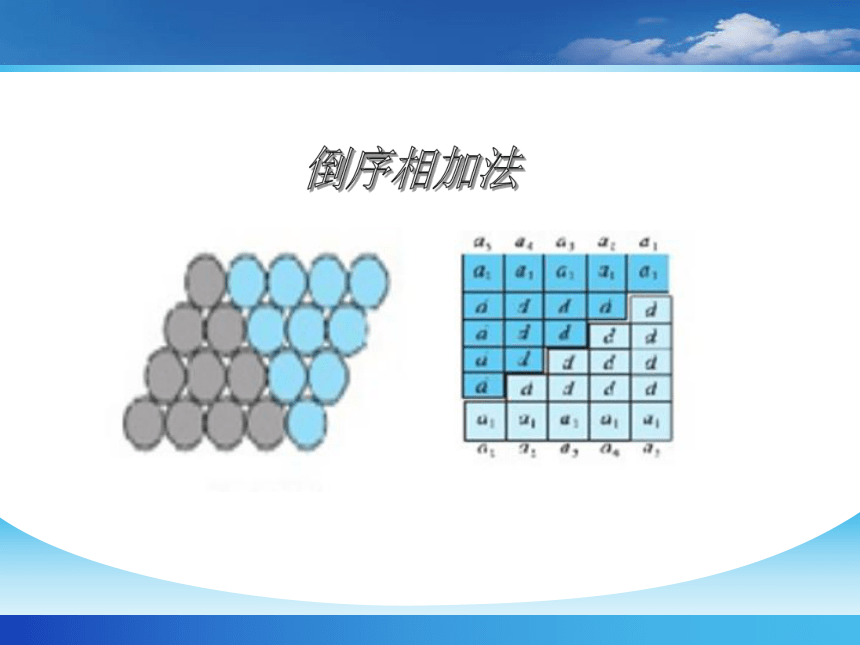
很快高斯便得出答案:5 050.老师大吃一惊,而更使人吃惊的是高斯的算法,高斯的算法是老师未曾教过的方法。那么这是一个什么样的方法呢?它用于解决什么类型的问题呢?这种方法叫倒序相加法,是等差数列求和的一种重要方法,本节我们就来研究它.情境导学倒序相加法思考:求前n个正整数的和。讲授新课倒序相加法在等差数列 中,若
m+n=p+q,则等于首末两项的和与项数乘积的一半倒序相加法若已知等差数列的首项,公差,项数三个量,
如何求等差数列的前n项和?推法2:通项公式法推法1:代入法等差数列的前n项和公式中, 共有几个基本 量?你认为须知几个量,才能求得其它量? 思考:例1 一个堆放铅笔的V形架的最下面一层放1支铅笔,
往上每一层都比它下面一层多放一支,最上面
一层放120支. 这个V形架上共放着多少支铅笔?例题讲解例2 课本15页的“问题提出”如图,有200根相同的圆木料,要把它们堆放成正三角形垛,并使剩余的圆木料尽可能的少,那么将剩余多少根圆木料?解:设共摆放了n层,能构成正三角形垛 的圆木料数为 则求满足题意的最大自然数n.所以n 的最大值是19,将堆垛19层,剩余10根圆木料。当堂检测: 课本第10页“问题提出”(1)一个剧场设置了20排座位,这个剧场从第一排起各排的座位数组成数列:
38,40,42,44,46,···
求剧场共有多少个座位?例3 课本16页例 7 求前n个正奇数的和。解:变3:
求前n个正
偶数的和。例4九五之尊指帝王之称,9是数字之极,5居正中,不偏不倚,若 峰,具鼎盛之势。 当堂检测
(课本17页练习1 第3题)1、倒序相加法 2、知三求二3、求等差数列前n项的和在实际生活中的应用归纳总结课后思考:课后作业:完成课本19页A组
预习本节第2课时
§2 等差数列
§2.2 等差数列的前n项和高斯
德国数学家,物理学家,天文学家,大地测量学家,
犹太民族。他是一位多产的数学家,光以“高斯”名字
命名的科研成果就有110项,有“数学王子”之称。
高斯与阿基米德、牛顿并列为历史上最伟大的数学家。
阿基米德
“力学之父”,他有一句与杠杆原理有关的名言是:“给我一个支点,我就能撬起整个地球。”
阿基米德原理:物体在液体中所受浮力等于它所排开液体的重量。
牛顿 苹果 万有引力 牛顿三大定律
他们都是百科全书式科学家。
多产数学家
数学王子
高斯“数学王子”高斯是德国数学家.在高斯10岁时,老师出了一道数学题:1到100的所有整数的和为多少?
很快高斯便得出答案:5 050.老师大吃一惊,而更使人吃惊的是高斯的算法,高斯的算法是老师未曾教过的方法。那么这是一个什么样的方法呢?它用于解决什么类型的问题呢?这种方法叫倒序相加法,是等差数列求和的一种重要方法,本节我们就来研究它.情境导学倒序相加法思考:求前n个正整数的和。讲授新课倒序相加法在等差数列 中,若
m+n=p+q,则等于首末两项的和与项数乘积的一半倒序相加法若已知等差数列的首项,公差,项数三个量,
如何求等差数列的前n项和?推法2:通项公式法推法1:代入法等差数列的前n项和公式中, 共有几个基本 量?你认为须知几个量,才能求得其它量? 思考:例1 一个堆放铅笔的V形架的最下面一层放1支铅笔,
往上每一层都比它下面一层多放一支,最上面
一层放120支. 这个V形架上共放着多少支铅笔?例题讲解例2 课本15页的“问题提出”如图,有200根相同的圆木料,要把它们堆放成正三角形垛,并使剩余的圆木料尽可能的少,那么将剩余多少根圆木料?解:设共摆放了n层,能构成正三角形垛 的圆木料数为 则求满足题意的最大自然数n.所以n 的最大值是19,将堆垛19层,剩余10根圆木料。当堂检测: 课本第10页“问题提出”(1)一个剧场设置了20排座位,这个剧场从第一排起各排的座位数组成数列:
38,40,42,44,46,···
求剧场共有多少个座位?例3 课本16页例 7 求前n个正奇数的和。解:变3:
求前n个正
偶数的和。例4九五之尊指帝王之称,9是数字之极,5居正中,不偏不倚,若 峰,具鼎盛之势。 当堂检测
(课本17页练习1 第3题)1、倒序相加法 2、知三求二3、求等差数列前n项的和在实际生活中的应用归纳总结课后思考:课后作业:完成课本19页A组
预习本节第2课时
