3.1等比数列(第一课时) 课件(27张PPT)
文档属性
| 名称 | 3.1等比数列(第一课时) 课件(27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 883.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-20 00:00:00 | ||
图片预览







文档简介
课件27张PPT。学段及学科:高中数学必修五
版 本:北师大版
课 题:第一章第三节等比数列
(第一课时)
§1.3.1 等比数列学习目标:1.理解等比数列的定义。
2.掌握等比数列的通项公式。会解决知道n, 中的三个,求另一个的问题。
学习重点:
1.等比数列概念的理解与掌握。
2.等比数列的通项公式的推导及应用。
一、创设情境,提出问题 情境一 如下图是某种细胞分裂的模型:细胞分裂个数可以组成下面的数列:1,2,4,8,16,…庄子曰:“一尺之棰,日取其半,万世不竭.”情境二意思:“一尺长的木棒,每日取其一半,永远也取不完” 。如果将“一尺之棰”视为一份,
则每日剩下的部分依次为: 某人从银行贷款10000元人民币,年利率为r,若此人一年后还款,二年后还款,三年后还款,……,还款数额依次满足什么规律?
10000(1+r),情境三10000(1+r)3,
…10000(1+r)2,
(1)1,2,4,8,….
观察上述情境所得的数列:?(3)10000(1+r), 10000 ,10000 ,… 问题2:仿照等差数列你能给这样的数列取个名字?问题1:(1)(2)(3)有何共同特征? 共同特征:从第二项起,每一项与它前面一项的比等于同一个常数。等比数列探究一:你能给等比数列下个定义吗?
(提示:类比等差数列的定义)等比数列的定义:如果一个数列从第2项起,每一项与它的前面一项的 都等于同一个常数,这个数列叫做 。 这个常数叫做 ,用 表示. 等比数列比公比二、归纳概括,形成概念
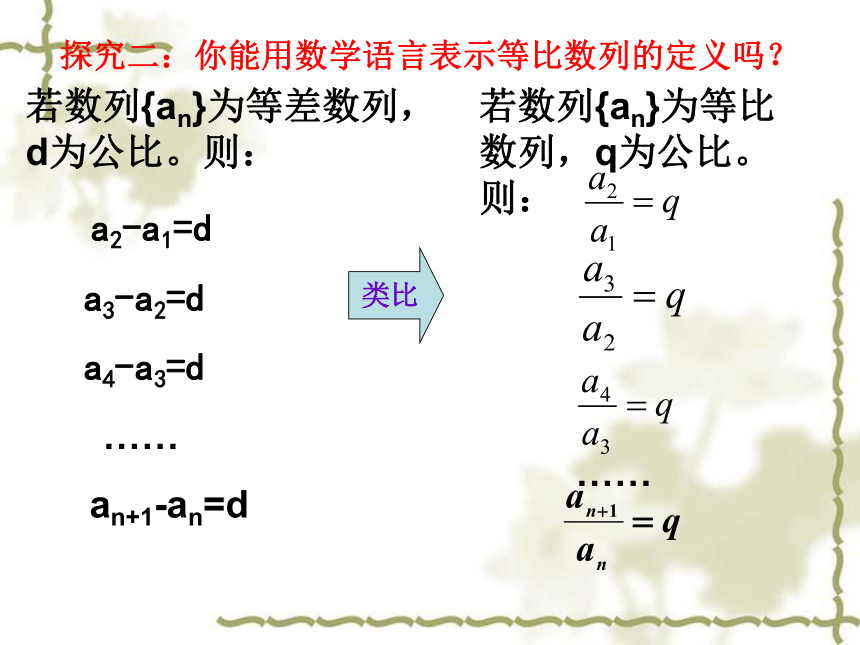
探究二:你能用数学语言表示等比数列的定义吗?类比若数列{an}为等比数列,q为公比。则:
……
若数列{an}为等差数列,d为公比。则:
a2-a1=d
a3-a2=d
a4-a3=d
……
an+1-an=d
等比数列的数学语言:定义的作用: 可用来判断或证明一个数列是不是等比数列。 例1 判断下列数列是否是等比数列?请说明理由。若是,公比是多少?
(1) ……
(2)1,2,4,8,16,20 ……
(3)1,1,1,1,1……
(4)-1,-2,-4,-8,-16;
(5)数列的通项公式为学以致用:三、启发诱导,深化概念 问题3:形如a,a,a,…( )的数列是 等差数列,那么是等比数列吗?
该数列一定是等差数列,但未必是等比数列。当a=0时,数列的每一项均为0,不能作比,因此不是等比数列;当a≠0时,此数列 为等比数列。 1、等比数列的各项均不为0,且公比也不为0。 注释:2、既是等差数列又是等比数列的是不等于零 的常数列。
四、等比数列的通项公式探究三:
在学习等差数列时,我们可以用公差d,项数n以及首项表示数列的任一项,也就是可以表示它的通项公式,那么在等比数列中,要表示该数列,需先确定几个条件?怎样用这些条件来表示这个等比数列的每一项?四、等比数列的通项公式法一:不完全归纳法……由此归纳等比数列的通项公式可得: 等比数列类比四、等比数列的通项公式: 累乘法……共n – 1 项×)等比数列类比an=a1qn-1等比数列的通项公式:
(n∈N﹡,q≠0)五、问题延伸问题4:对于这个通项公式,我们可以从哪几个方面去认识它呢?
(2)还可以从方程观点去认识,把通项看成一个方程。
公式中有四个基本量: ,可“知三求一”,体现方程思想。 (1)可以从函数观点去认识,把通项看成 n的解析式。目的是让学生更好的区别等比数列与等差数列的特征。例2、在等比数列{an}中,已知:
求an ?学以致用:
解:设等比数列{an}的公比为q,由题意得规范解答:
解得因此,
例3、一个等比数列的首相是2,第2项与第3项的和是12。求它的第8项的值?
学以致用:
解 设等比数列的首相是a1,公比是q,
则有已知,得
a1=2 ①
a1q +a1q2=12 ②
将 ①式代入②式,得 q2+q-6=0
解得 q=-3或q=2.
当q=-3时,a8=a1q7=2*(-3)7=-4374
当q=2时,a8=a1q7=2*27=28=256
故数列的第8项是-4374或256。规范解答:
六、课堂练习1 、 课本第23页练习1
2 、 已知数列 是等比数列,
,求 的值。课堂小结:课堂小结:1.等比数列的定义:(1)归纳法;(2)累乘法。推导方法:2.等比数列的通项公式:公式的认识:(1)函数的观点;(2)方程的思想。an=a1qn-1 课后作业:
必作:课本第30页习题1--3,A组 1、2、3、7、8
选作:已知数列 满足
(1)求证: 是等比数列。
(2)求数列 的通项?
课后思考:对照等差数列,试猜想等比数列的一些相应性质。
祝同学们自今日起,学业成正等比数列指数爆炸式递增!
前途焦虑压力成负等比数列指数爆炸式递减!
版 本:北师大版
课 题:第一章第三节等比数列
(第一课时)
§1.3.1 等比数列学习目标:1.理解等比数列的定义。
2.掌握等比数列的通项公式。会解决知道n, 中的三个,求另一个的问题。
学习重点:
1.等比数列概念的理解与掌握。
2.等比数列的通项公式的推导及应用。
一、创设情境,提出问题 情境一 如下图是某种细胞分裂的模型:细胞分裂个数可以组成下面的数列:1,2,4,8,16,…庄子曰:“一尺之棰,日取其半,万世不竭.”情境二意思:“一尺长的木棒,每日取其一半,永远也取不完” 。如果将“一尺之棰”视为一份,
则每日剩下的部分依次为: 某人从银行贷款10000元人民币,年利率为r,若此人一年后还款,二年后还款,三年后还款,……,还款数额依次满足什么规律?
10000(1+r),情境三10000(1+r)3,
…10000(1+r)2,
(1)1,2,4,8,….
观察上述情境所得的数列:?(3)10000(1+r), 10000 ,10000 ,… 问题2:仿照等差数列你能给这样的数列取个名字?问题1:(1)(2)(3)有何共同特征? 共同特征:从第二项起,每一项与它前面一项的比等于同一个常数。等比数列探究一:你能给等比数列下个定义吗?
(提示:类比等差数列的定义)等比数列的定义:如果一个数列从第2项起,每一项与它的前面一项的 都等于同一个常数,这个数列叫做 。 这个常数叫做 ,用 表示. 等比数列比公比二、归纳概括,形成概念
探究二:你能用数学语言表示等比数列的定义吗?类比若数列{an}为等比数列,q为公比。则:
……
若数列{an}为等差数列,d为公比。则:
a2-a1=d
a3-a2=d
a4-a3=d
……
an+1-an=d
等比数列的数学语言:定义的作用: 可用来判断或证明一个数列是不是等比数列。 例1 判断下列数列是否是等比数列?请说明理由。若是,公比是多少?
(1) ……
(2)1,2,4,8,16,20 ……
(3)1,1,1,1,1……
(4)-1,-2,-4,-8,-16;
(5)数列的通项公式为学以致用:三、启发诱导,深化概念 问题3:形如a,a,a,…( )的数列是 等差数列,那么是等比数列吗?
该数列一定是等差数列,但未必是等比数列。当a=0时,数列的每一项均为0,不能作比,因此不是等比数列;当a≠0时,此数列 为等比数列。 1、等比数列的各项均不为0,且公比也不为0。 注释:2、既是等差数列又是等比数列的是不等于零 的常数列。
四、等比数列的通项公式探究三:
在学习等差数列时,我们可以用公差d,项数n以及首项表示数列的任一项,也就是可以表示它的通项公式,那么在等比数列中,要表示该数列,需先确定几个条件?怎样用这些条件来表示这个等比数列的每一项?四、等比数列的通项公式法一:不完全归纳法……由此归纳等比数列的通项公式可得: 等比数列类比四、等比数列的通项公式: 累乘法……共n – 1 项×)等比数列类比an=a1qn-1等比数列的通项公式:
(n∈N﹡,q≠0)五、问题延伸问题4:对于这个通项公式,我们可以从哪几个方面去认识它呢?
(2)还可以从方程观点去认识,把通项看成一个方程。
公式中有四个基本量: ,可“知三求一”,体现方程思想。 (1)可以从函数观点去认识,把通项看成 n的解析式。目的是让学生更好的区别等比数列与等差数列的特征。例2、在等比数列{an}中,已知:
求an ?学以致用:
解:设等比数列{an}的公比为q,由题意得规范解答:
解得因此,
例3、一个等比数列的首相是2,第2项与第3项的和是12。求它的第8项的值?
学以致用:
解 设等比数列的首相是a1,公比是q,
则有已知,得
a1=2 ①
a1q +a1q2=12 ②
将 ①式代入②式,得 q2+q-6=0
解得 q=-3或q=2.
当q=-3时,a8=a1q7=2*(-3)7=-4374
当q=2时,a8=a1q7=2*27=28=256
故数列的第8项是-4374或256。规范解答:
六、课堂练习1 、 课本第23页练习1
2 、 已知数列 是等比数列,
,求 的值。课堂小结:课堂小结:1.等比数列的定义:(1)归纳法;(2)累乘法。推导方法:2.等比数列的通项公式:公式的认识:(1)函数的观点;(2)方程的思想。an=a1qn-1 课后作业:
必作:课本第30页习题1--3,A组 1、2、3、7、8
选作:已知数列 满足
(1)求证: 是等比数列。
(2)求数列 的通项?
课后思考:对照等差数列,试猜想等比数列的一些相应性质。
祝同学们自今日起,学业成正等比数列指数爆炸式递增!
前途焦虑压力成负等比数列指数爆炸式递减!
