3.1等比数列 课件(21张PPT)
文档属性
| 名称 | 3.1等比数列 课件(21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 396.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-20 22:01:58 | ||
图片预览







文档简介
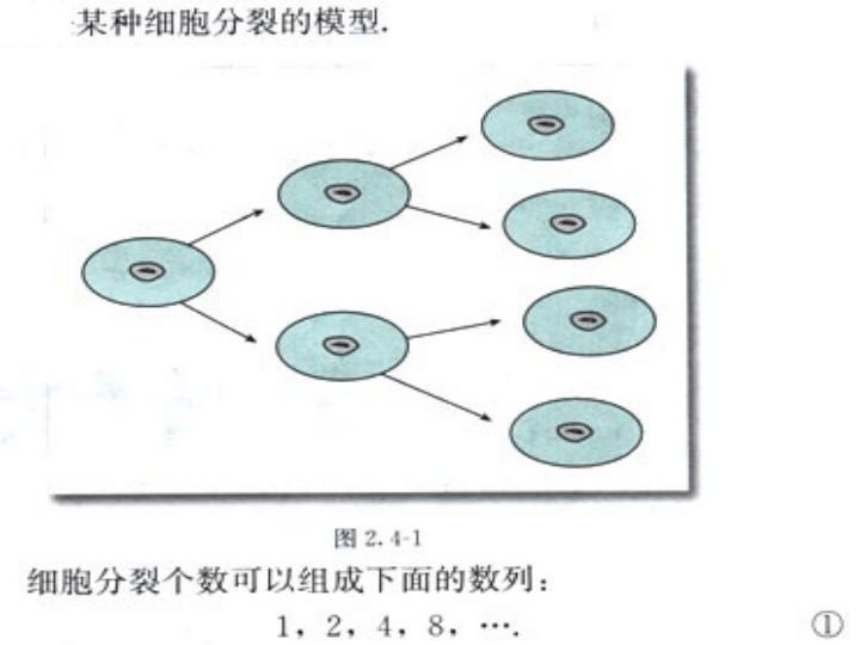
课件21张PPT。 袁隆平在培育某水稻新品种时,培育出第一代120粒种子,并且从第一代起,由以后各代的每一粒种子都可以得到下一代的120粒种子,到第5代时大约可以得到这个新品种的种子多少粒,你可以解决这个问题吗?我们将用到什么样的数学知识呢?世界杂交水稻之父—袁隆平等 比 数 列 知识回顾从第2项起,每一项与它的前一项的差都等于同一个常数
公差(d)d可正可负,也可以为零创设情景,引入新课(1)我国古代学者提出:“一尺 之棰,日取其半,万世不竭。”用现代语言叙述为:一尺长的木棒,每日取其一半,永远也取不完。这样,每日剩下的部分都是前一日的一半。如果把“一尺之棰”看成单位“1”,那么,得到的数列是:
1, , , ,┉ 。 一位数学家说过:你如果能将一张纸对折38次,我就能顺着它在今天晚上爬上月球。如果一页纸厚度看成单位“1”,那么,得到纸的厚度形成的数列为:
1,---,---,---,---以上两个实例所包含的两个数列如下:
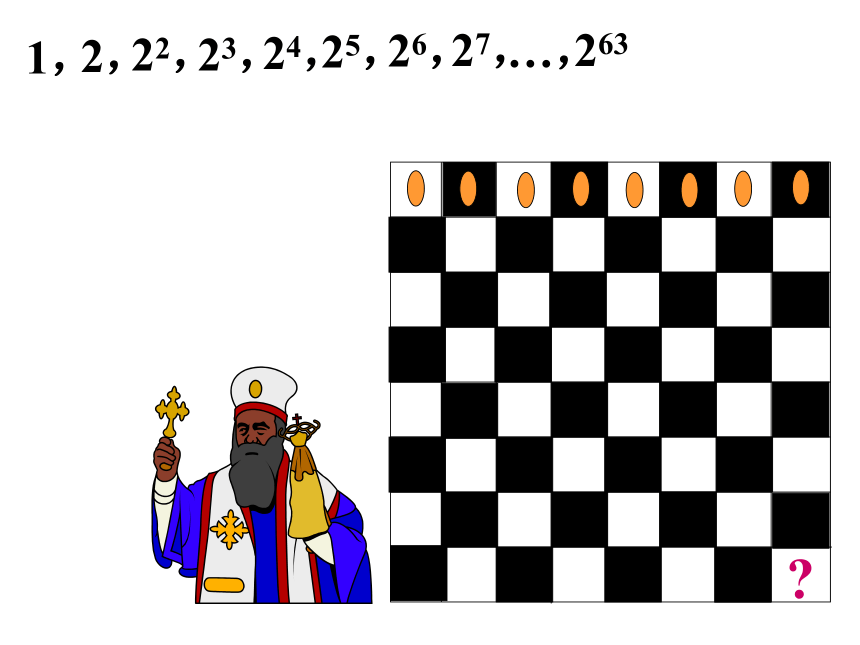
一般地,如果一个数列从第2项起,每一项与它的前一项的 比 等于同一个常数,那么这个数列就叫做等比数列 ,这个常数叫做等比数列的公比(q)。 一般地,如果一个数列从第2项起,每一项与它的前一项的 差 等于同一个常数,那么这个数列就叫做等差数列 ,这个常数叫做等差数列的公差(d)。等比数列等差数列等比数列概念课堂互动(一)你能抽象出下列实际问题所形成的数列吗?它们是等比数列吗?1,2,22,23,24,25,26,27,…,?263某市近10年的国内生产总值从2000亿元开始,每年以10%的速度增长,近十年的国内生产总值(单位:亿元)分别是: (1)5,25,125,625…;
(2)1,-1,- 1,-1…;
(3)1,1,1,1,…;
(4)1,2,4,8,12, 16, 20;
(5)1,-1,1,-1,1,-1…;
(6)0,0,0,0…;
(7)a,a,a,a,a…。看下列数列,问是否为等比数列,如果是,写出公比: 结论(1)q=1时为常数数列
(2)q>0时各项与首项同号
(3)q<0时各项正负相间 是, q=5;不是;是, q=1;不是; 是, q=-1;不是;不一定。课堂互动(二)(1) 1,3,9,27,…(3) 5, 5, 5, 5,…(4) 1,-1,1,-1,…(2) (5) 1,0,1,0,…(6) 0,0,0,0,…1. 各项不能为零,即 2. 公比不能为零,即4. 数列 a, a , a , …时,既是等差数列
又是等比数列;时,只是等差数列而不是等比数列.3. 当q>0,各项与首项同号
当q<0,各项符号正负相间对概念的更深理解注意等差数列通项公式的推导:方法一:(叠加法)等比数列通项公式的推导:(n-1)个 式子… …方法一:叠乘法… …方法二:归纳法等比数列通项公式的推导:特别地,等比数列{an}中,a1≠0,q≠0等比数列的通项公式:
例1 袁隆平在培育某水稻新品种时,培育出第一代120粒种子,并且从第一代起,由以后各代的每一粒种子都可以得到下一代的120粒种子,到第5代时大约可以得到这个新品种的种子多少粒(保留两位有效数字)?由于每代的种子数是它的前一代种子数的120倍,因此,逐代的种子数组成等比数列,记为 答:到第5代大约可以得到这种新品种的种子2.5×1010粒.解:例题讲解:解:用{an} 表示题中公比为q的等比数列,由已知条件,有 解得 因此, 答:这个数列的第1项与第2项分别是例2.一个等比数列的第3项和第4项分别是12和18,求它的第1项和第2项.练习.等比数列{an}中, a1=2,a2+a3=12, 求a8.解:设等比数列的公比为q,则由已知得:
a1=2 (1)
a1q+a1q2=12 (2)
将(1)代入(2)式得q2+q-6=0,解得q=-3或q=2. 当q=-3时, a8=a1.q7=-4374, 当q=2时, a8=a1.q7=256.本节课你学到了什么?等比数列的概念;
等比数列的通项公式及其简单应用;
类比思想的运用。
作业:课本第30页 A组:3, 6.谢谢大家!再见!
公差(d)d可正可负,也可以为零创设情景,引入新课(1)我国古代学者提出:“一尺 之棰,日取其半,万世不竭。”用现代语言叙述为:一尺长的木棒,每日取其一半,永远也取不完。这样,每日剩下的部分都是前一日的一半。如果把“一尺之棰”看成单位“1”,那么,得到的数列是:
1, , , ,┉ 。 一位数学家说过:你如果能将一张纸对折38次,我就能顺着它在今天晚上爬上月球。如果一页纸厚度看成单位“1”,那么,得到纸的厚度形成的数列为:
1,---,---,---,---以上两个实例所包含的两个数列如下:
一般地,如果一个数列从第2项起,每一项与它的前一项的 比 等于同一个常数,那么这个数列就叫做等比数列 ,这个常数叫做等比数列的公比(q)。 一般地,如果一个数列从第2项起,每一项与它的前一项的 差 等于同一个常数,那么这个数列就叫做等差数列 ,这个常数叫做等差数列的公差(d)。等比数列等差数列等比数列概念课堂互动(一)你能抽象出下列实际问题所形成的数列吗?它们是等比数列吗?1,2,22,23,24,25,26,27,…,?263某市近10年的国内生产总值从2000亿元开始,每年以10%的速度增长,近十年的国内生产总值(单位:亿元)分别是: (1)5,25,125,625…;
(2)1,-1,- 1,-1…;
(3)1,1,1,1,…;
(4)1,2,4,8,12, 16, 20;
(5)1,-1,1,-1,1,-1…;
(6)0,0,0,0…;
(7)a,a,a,a,a…。看下列数列,问是否为等比数列,如果是,写出公比: 结论(1)q=1时为常数数列
(2)q>0时各项与首项同号
(3)q<0时各项正负相间 是, q=5;不是;是, q=1;不是; 是, q=-1;不是;不一定。课堂互动(二)(1) 1,3,9,27,…(3) 5, 5, 5, 5,…(4) 1,-1,1,-1,…(2) (5) 1,0,1,0,…(6) 0,0,0,0,…1. 各项不能为零,即 2. 公比不能为零,即4. 数列 a, a , a , …时,既是等差数列
又是等比数列;时,只是等差数列而不是等比数列.3. 当q>0,各项与首项同号
当q<0,各项符号正负相间对概念的更深理解注意等差数列通项公式的推导:方法一:(叠加法)等比数列通项公式的推导:(n-1)个 式子… …方法一:叠乘法… …方法二:归纳法等比数列通项公式的推导:特别地,等比数列{an}中,a1≠0,q≠0等比数列的通项公式:
例1 袁隆平在培育某水稻新品种时,培育出第一代120粒种子,并且从第一代起,由以后各代的每一粒种子都可以得到下一代的120粒种子,到第5代时大约可以得到这个新品种的种子多少粒(保留两位有效数字)?由于每代的种子数是它的前一代种子数的120倍,因此,逐代的种子数组成等比数列,记为 答:到第5代大约可以得到这种新品种的种子2.5×1010粒.解:例题讲解:解:用{an} 表示题中公比为q的等比数列,由已知条件,有 解得 因此, 答:这个数列的第1项与第2项分别是例2.一个等比数列的第3项和第4项分别是12和18,求它的第1项和第2项.练习.等比数列{an}中, a1=2,a2+a3=12, 求a8.解:设等比数列的公比为q,则由已知得:
a1=2 (1)
a1q+a1q2=12 (2)
将(1)代入(2)式得q2+q-6=0,解得q=-3或q=2. 当q=-3时, a8=a1.q7=-4374, 当q=2时, a8=a1.q7=256.本节课你学到了什么?等比数列的概念;
等比数列的通项公式及其简单应用;
类比思想的运用。
作业:课本第30页 A组:3, 6.谢谢大家!再见!
