3.1基本不等式 课件(17张PPT)
文档属性
| 名称 | 3.1基本不等式 课件(17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 855.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-20 00:00:00 | ||
图片预览


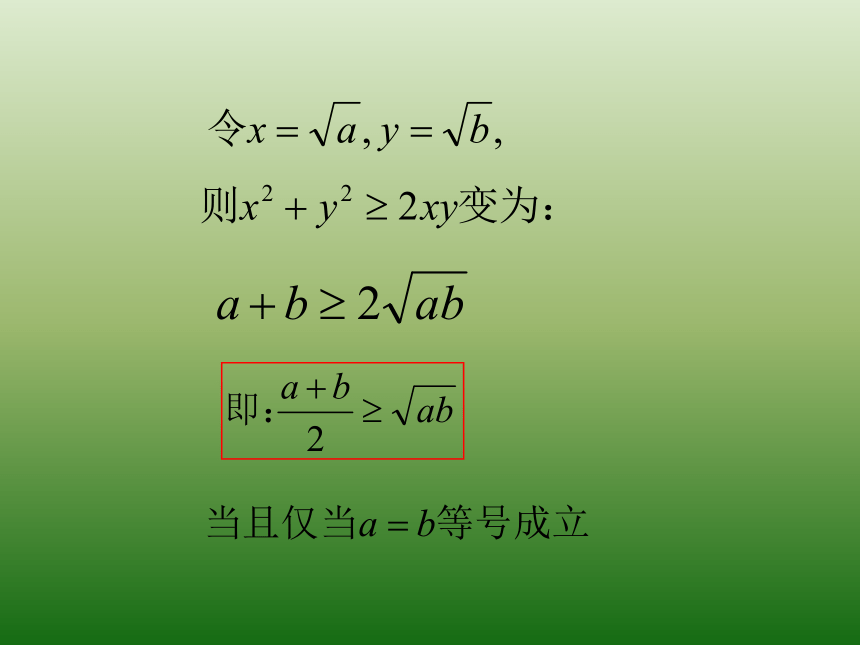


文档简介
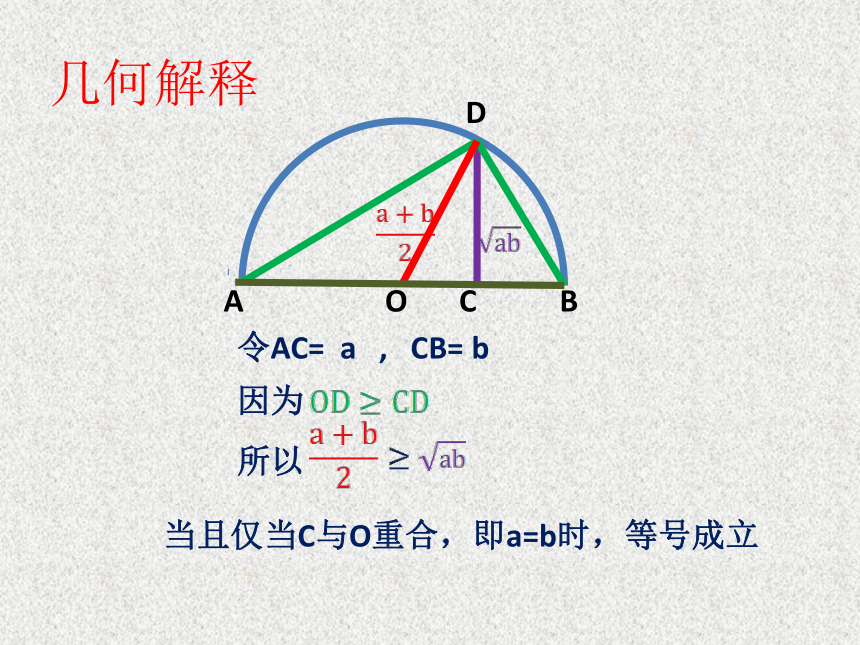
课件17张PPT。国际数学大会(ICM2002)的会标赵爽弦图ABCD正方形ABCD的面积≥4个直角三角形面积之和EFGHACBDO令AC= a , CB= b因为所以当且仅当C与O重合,即a=b时,等号成立几何解释对基本不等式,用语言文字可叙述为:两个非负数的算术平均数不小于它们的几何平均数。从几何的角度可叙述为:圆的半径不小于弦长的一半。从数列的角度可叙述为:两个正数的等差中项不小于它们的等比中项。 设a,b均为正数,
证明不等式 证法1 :因为a,b均为正数,由基本不等式,即当且仅当a=b时,等号成立典例分析 设a,b均为正数,
证明不等式 证法2 :因为a,b均为正数 即当且仅当a=b时,等号成立典例分析所以几何解释故当且仅当C与O重合,即a=b时,等号成立ACBDO令AC= a , CB= b因为所以当且仅当C与O重合,即a=b时,等号成立又思考交流想一想? 由基本不等式,例题和思考交流你能给出这几个式子的大小关系吗?
当且仅当a,b正实数,a=b时,等号成立牛刀小试牛刀小试课后思考:1、学习课本89页阅读材料,探讨与所学不等式有何关系?与实际生活有何联系?2、动手实践:研究有课本90页练习题能得出什么结论?与所学不等式有何关系?小结1.两个重要的不等式2.对基本不等式和例1及思考交流的总结当且仅当a=b时,等号成立当且仅当a,b正实数,a=b时,等号成立作 业
1.思考题
2.课本94页A组第3题、B组第1题
么惠芳感谢聆听、敬请指导!
当且仅当a,b正实数,a=b时,等号成立牛刀小试牛刀小试课后思考:1、学习课本89页阅读材料,探讨与所学不等式有何关系?与实际生活有何联系?2、动手实践:研究有课本90页练习题能得出什么结论?与所学不等式有何关系?小结1.两个重要的不等式2.对基本不等式和例1及思考交流的总结当且仅当a=b时,等号成立当且仅当a,b正实数,a=b时,等号成立作 业
1.思考题
2.课本94页A组第3题、B组第1题
么惠芳感谢聆听、敬请指导!
