3.1基本不等式 课件（23张PPT）

课件23张PPT。创设情境 引入新课 为了在校园内的空地上开发出一块面积为100平方米矩形花园，并用篱笆围起保护花草，你认为如何设计花园的长和宽，能使所用篱笆最短，最短为多少？
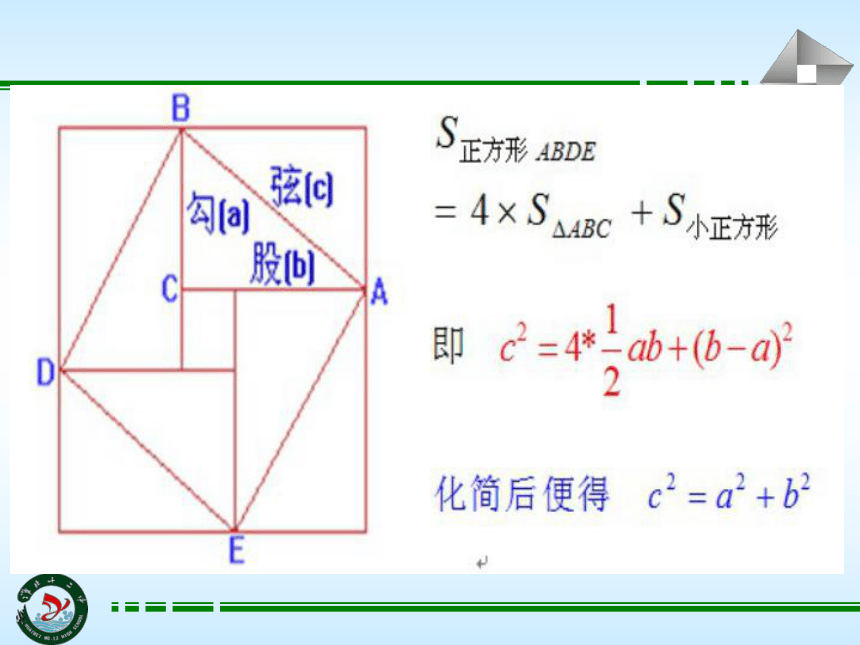
3.1 基本不等式如图，是在北京召开的第24届国际数学家大会会标．风车，寓意代表中国人民热情好客.观察思考ICM2002会标赵爽：弦图探究新知赵爽：又名婴，字 君卿，东汉末至三国时代吴国人，是我国历史上著名的数学家与天文学家。ICM2002会标赵爽：弦图探究新知问题1： 您能从会标中抽象出什么样的几何图形？ 问题2、你还能从面积角度在会标中找出一些相等关系和不等关系吗？a2+b2＞2ab四个直角三角形面积相等，和为：2ab正方形ABCD的面积为：a2+b2探究新知探究新知问题3：当小正方形的四个顶点EFGH缩为一个点时，又有何关系？问题4：
能否推广到对于任意实数 ，
都成立呢？ 探究新知形数几何解释代数证明探究新知
数与形,本是相倚依,
焉能分作两边飞;
数无形时少直觉,
形少数时难入微;
数形结合百般好,
隔离分家万事休;
切莫忘,几何代数统一体,
永远联系莫分离.
——华罗庚问题5：
当 时，能用 、 分别代替
中的 、 吗？若能，又会得到什么结果呢？ 运用新知、深入探究： 我们可以通过弦
图给予几何解释，
那么
也能有它合理的几何解释吗？
问题6：运用新知 深入探究 已知AB是圆O的直径，过圆上任意一点D作AB的垂线DE交AB于点C，连接AD、BD，AC=a,CB=b.你能利用这个圆形，求OD,CD的长几何解释CD=OD=CD≤ OD几何解释 时等号成立学以致用 解决生活：学以致用例2、用一段长为36 m的篱笆围成一个矩形菜园，如何设计篱笆的长和宽，菜园的面积最大？最大面积是多少?1、本节课你学到了哪些数学知识？2、本节课你学到哪些数学思想方法？ 总结提炼、归纳新知：布置作业1、课本P94习题3.3A组第1、4题。
2、设 均为正数，比较下列各式的大小
谢谢