数列前n项和常见求解方法 课件(18张PPT)
文档属性
| 名称 | 数列前n项和常见求解方法 课件(18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-20 22:32:58 | ||
图片预览





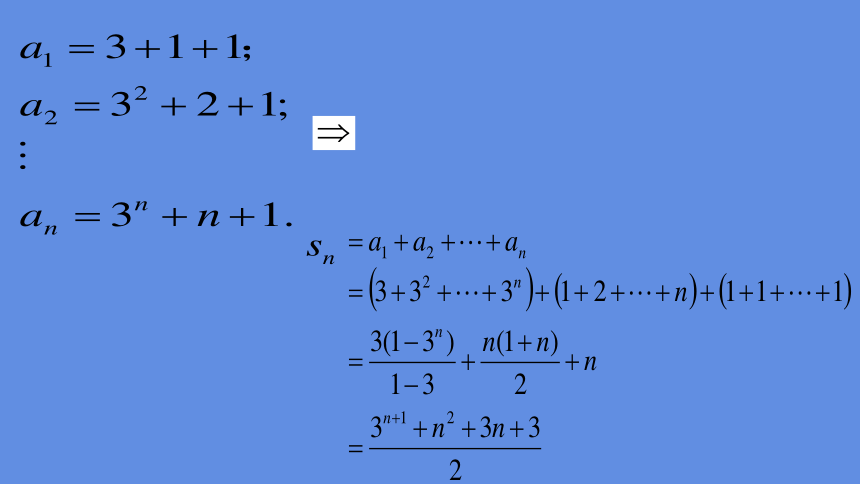

文档简介
课件18张PPT。数列前n项和的常见求解方法 年级:高一(24)班教材:北师大版 必修5一、公式法1、如果一个数列是等差数列:
递推关系
前n项和:
2、如果一个数列是等比数列:
递推关系
前n项和: 二、分组求和与并项求和若一个数列的通项公式是由若干个等差数列或等比数列或可求和的数列组成,则求和时可用分组转化法,分别求和而后相加减.
例1:数列 , ,求数列
的前n项和 .
解:
·并项求和是将原数列的项重新组合,
使他们成为一个或几个等差或等比数
列再求和的方法。例、已知数列
求
解 :
三、倒序相加法如果一个数列{an},首末两端等“距离”的两项的和相等或等于同一常数,那么求这个数列的前n项和即可用倒序相加法,如等差数列的前n项和即是用此法推导的.四、错位相减法 如果一个数列的各项是由一个等差数列和一个等比数列的对应项之积构成的,那么这个数列的前n项和即可用此法来求.
例4:设 {an}的前n项和为Sn,an=n·2n,则求数列{an}的前n项和Sn 例4:设 {an}的前n项和为Sn,an=n·2n,则求数列{an}的前n项和Sn 作业: 谢谢!五、裂项相消法 把数列的通项拆成两项之差,在求和时中间的一些项可以相互抵消,从而求得其和.
例5、设 {an}的前n项和为Sn,an= ,则求数列{an}的前n项和Sn .
作业:
递推关系
前n项和:
2、如果一个数列是等比数列:
递推关系
前n项和: 二、分组求和与并项求和若一个数列的通项公式是由若干个等差数列或等比数列或可求和的数列组成,则求和时可用分组转化法,分别求和而后相加减.
例1:数列 , ,求数列
的前n项和 .
解:
·并项求和是将原数列的项重新组合,
使他们成为一个或几个等差或等比数
列再求和的方法。例、已知数列
求
解 :
三、倒序相加法如果一个数列{an},首末两端等“距离”的两项的和相等或等于同一常数,那么求这个数列的前n项和即可用倒序相加法,如等差数列的前n项和即是用此法推导的.四、错位相减法 如果一个数列的各项是由一个等差数列和一个等比数列的对应项之积构成的,那么这个数列的前n项和即可用此法来求.
例4:设 {an}的前n项和为Sn,an=n·2n,则求数列{an}的前n项和Sn 例4:设 {an}的前n项和为Sn,an=n·2n,则求数列{an}的前n项和Sn 作业: 谢谢!五、裂项相消法 把数列的通项拆成两项之差,在求和时中间的一些项可以相互抵消,从而求得其和.
例5、设 {an}的前n项和为Sn,an= ,则求数列{an}的前n项和Sn .
作业:
