必修5 第一章数列 小结与复习 课件(18张PPT)
文档属性
| 名称 | 必修5 第一章数列 小结与复习 课件(18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 170.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-20 22:04:51 | ||
图片预览






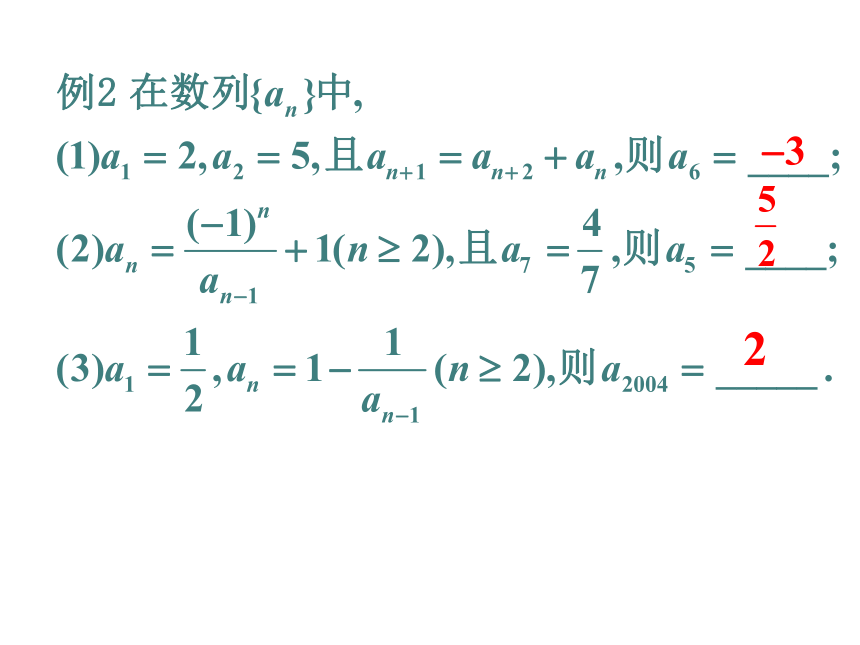
文档简介
课件18张PPT。《数列》小结与复习一教学目标:1、知识与技能:⑴进一步理解数列基础知识和方法,能清晰地构思解决问题的方案;⑵进一步学习有条理地、清晰地表达数学问题,提高逻辑思维能力;⑶加强对等差数列与等比数列的性质的理解,提高“知三求二”的熟练程度;⑷在理解的基础上进一步熟练地构建数列模型解决实际问题。2、过程与方法:⑴通过实例,发展对解决具体问题的过程与步骤进行分析的能力;⑵通过独立思考、合作交流、自主探究的过程,发展应用数列基础知识的能力;⑶在解决具体问题的过程中更进一步地感受数列问题中蕴含的思想方法。3、情感态度与价值观:⑴通过具体实例,感受和体会数列在解决具体问题中的意义和作用,认识数列知识的重要性;⑵感受并认识数列知识的重要作用,形成自觉地将数学知识与实际问题相结合的?思想;⑶在解决实际问题过程中形成和发展正确的价值观
二、教学重点 1.系统化本章的知识结构;2.提高对几种常见类型的认识;3.优化解题思路和解题方法,提升数学表达的能力。教学难点 解题思路和解题方法的优化。
三、教学方法:探究归纳,讲练结合
四、教学过程知识结构数列数
列
的
应
用数列求和等比数列前n项和公式性质定义等差数列通项公式递推公式数列的概念通项公式前n项和公式性质定义通项公式知识归纳1.数列的概念:
(1)按一定次序排成的列数称为数列.
(2)表示方法主要有:通项公式法,递推公式法,前n项和法,和图像法等.(图像是自变量取正整数的一些孤立的点)
2.等差数列:
(1)定义:an+1-an=常数
(2)通项公式:an=a1+(n-1)d 推广: an=am+(n-m)d
(3)前n项和公式:
(4)性质:①若m+n=p+q,则am+an=ap+aq
②若数列{an}是等差数列,则
也是等差数列
③等差数列{an}的任意等距离的项构成的数列仍为等差数列
3.等比数列:
(1)定义:an+1/an=常数
(2)通项公式:an=a1qn-1 推广: an=amqn-m
(3)前n项和公式:
(4)性质:①若m+n=p+q,则aman=apaq
②若数列{an}是等比数列,则
也是等比数列
③等比数列{an}的任意等距离的项构成的数列仍为等比数列
4. 数列求和:
常用求和方法:裂项求和、分组求和、错位相减、倒序相加例1 根据数列的前几项,写出下列数列的一个通项公式:求通项(3)累差法或累积法求解例4 (1)设数列 前n项的和求 的通项公式. 换元法性质的应用 已知等差数列中的任意两项,可以求出其他的元素.这里应用的是方程组的思想.例5102724例6 在等比数列 中,(1)若 则(2)若 则(4)若 则(3)已知 求3050324例7数列的应用例8 购买一件售价为5000元的商品,采用分期付款的办法,每期付款数相同,购买后1个月付款一次,过1个月再付款一次,如此下去,到第12次付款后全部付清.如果月利率为0.8%,每月利息按复利计算(上月利息计入下月本金),那么每期应付款多少元?(精确到1元)解:设每期应付款x元,则
第一期与到最后一期付款所生利息之和为x(1+1.008)11元;
第二期与到最后一期付款所生利息之和为x(1+1.008)10元;
… …
第十一期与到最后一期付款所生利息之和为x(1+1.008) 元;
第十二期付款已没有利息问题,即为x元.
所以各期付款连同利息之和为
又所购商品的售价及其利息之和为5000×1.00812
于是有
答:每期应付款约439元.小结1.等差数列的基本公式在数列中占用重要的地位,应用要从公式的正向、逆向、变式等多角度去思考.
2.等比数列的前n项和公式要分两种情况,公比等于1和公比不等于1,而公比等于1的情况最容易忽略.
3.等差数列和等比数列中,经常要根据条件列方程(组)
求解,注意用方程的思想、消元的思想及整体代换思想分析问题和解决问题.
4.数列的渗透力很强,它和函数、方程、三角、不等式等知识相互联系,优化组合.解题是必须深刻体会蕴藏在数列概念和方法中的数学思想,如函数与方程、数形结合、分类讨论、等价转化等.课堂小结:本节学习了如下内容:1.第二章“数列”一章知识和方法的概括性回顾与思考.2.运用中典型例题的探究。
布置作业:课本复习参考题一 A组13、14 B组5?
五、教学反思:
二、教学重点 1.系统化本章的知识结构;2.提高对几种常见类型的认识;3.优化解题思路和解题方法,提升数学表达的能力。教学难点 解题思路和解题方法的优化。
三、教学方法:探究归纳,讲练结合
四、教学过程知识结构数列数
列
的
应
用数列求和等比数列前n项和公式性质定义等差数列通项公式递推公式数列的概念通项公式前n项和公式性质定义通项公式知识归纳1.数列的概念:
(1)按一定次序排成的列数称为数列.
(2)表示方法主要有:通项公式法,递推公式法,前n项和法,和图像法等.(图像是自变量取正整数的一些孤立的点)
2.等差数列:
(1)定义:an+1-an=常数
(2)通项公式:an=a1+(n-1)d 推广: an=am+(n-m)d
(3)前n项和公式:
(4)性质:①若m+n=p+q,则am+an=ap+aq
②若数列{an}是等差数列,则
也是等差数列
③等差数列{an}的任意等距离的项构成的数列仍为等差数列
3.等比数列:
(1)定义:an+1/an=常数
(2)通项公式:an=a1qn-1 推广: an=amqn-m
(3)前n项和公式:
(4)性质:①若m+n=p+q,则aman=apaq
②若数列{an}是等比数列,则
也是等比数列
③等比数列{an}的任意等距离的项构成的数列仍为等比数列
4. 数列求和:
常用求和方法:裂项求和、分组求和、错位相减、倒序相加例1 根据数列的前几项,写出下列数列的一个通项公式:求通项(3)累差法或累积法求解例4 (1)设数列 前n项的和求 的通项公式. 换元法性质的应用 已知等差数列中的任意两项,可以求出其他的元素.这里应用的是方程组的思想.例5102724例6 在等比数列 中,(1)若 则(2)若 则(4)若 则(3)已知 求3050324例7数列的应用例8 购买一件售价为5000元的商品,采用分期付款的办法,每期付款数相同,购买后1个月付款一次,过1个月再付款一次,如此下去,到第12次付款后全部付清.如果月利率为0.8%,每月利息按复利计算(上月利息计入下月本金),那么每期应付款多少元?(精确到1元)解:设每期应付款x元,则
第一期与到最后一期付款所生利息之和为x(1+1.008)11元;
第二期与到最后一期付款所生利息之和为x(1+1.008)10元;
… …
第十一期与到最后一期付款所生利息之和为x(1+1.008) 元;
第十二期付款已没有利息问题,即为x元.
所以各期付款连同利息之和为
又所购商品的售价及其利息之和为5000×1.00812
于是有
答:每期应付款约439元.小结1.等差数列的基本公式在数列中占用重要的地位,应用要从公式的正向、逆向、变式等多角度去思考.
2.等比数列的前n项和公式要分两种情况,公比等于1和公比不等于1,而公比等于1的情况最容易忽略.
3.等差数列和等比数列中,经常要根据条件列方程(组)
求解,注意用方程的思想、消元的思想及整体代换思想分析问题和解决问题.
4.数列的渗透力很强,它和函数、方程、三角、不等式等知识相互联系,优化组合.解题是必须深刻体会蕴藏在数列概念和方法中的数学思想,如函数与方程、数形结合、分类讨论、等价转化等.课堂小结:本节学习了如下内容:1.第二章“数列”一章知识和方法的概括性回顾与思考.2.运用中典型例题的探究。
布置作业:课本复习参考题一 A组13、14 B组5?
五、教学反思:
