2 角的概念与推广 课件(26张PPT)
文档属性
| 名称 | 2 角的概念与推广 课件(26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 950.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-20 00:00:00 | ||
图片预览






文档简介
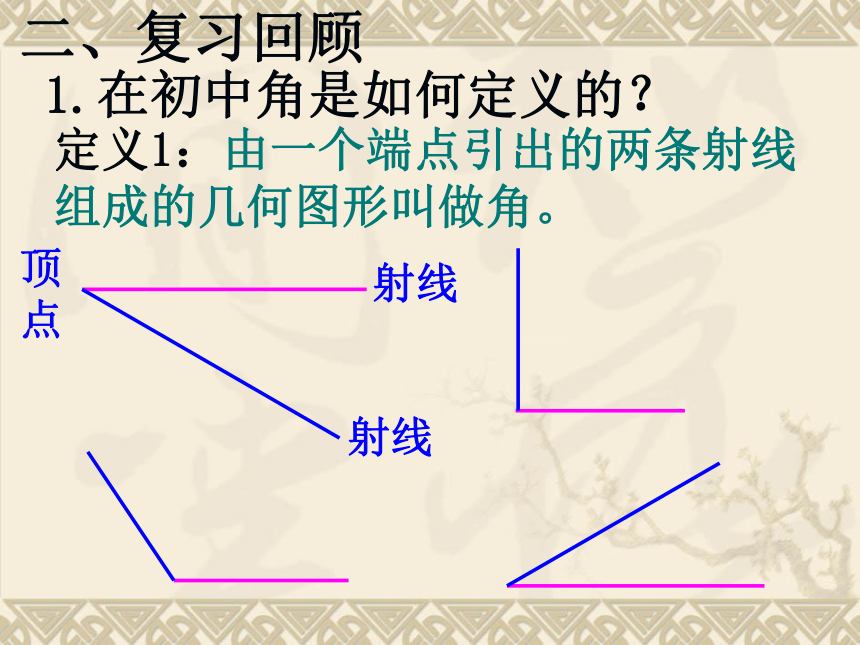
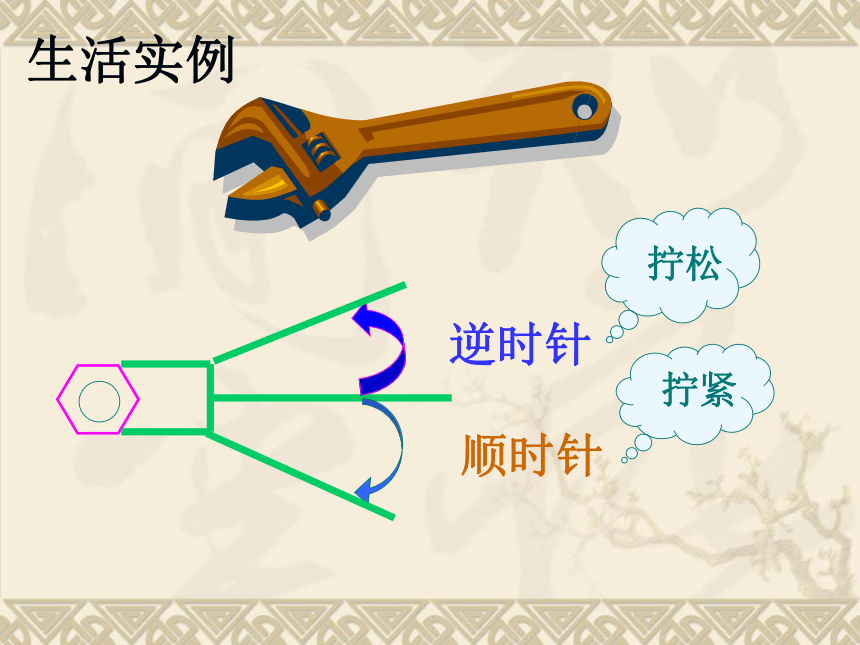
课件26张PPT。§2 角的概念推广生活剪影奥运五环 一、创设情境 引入新课1.在初中角是如何定义的?定义1:由一个端点引出的两条射线组成的几何图形叫做角。顶点射线射线二、复习回顾 角可以看做:平面内一条射线绕着它的端点从一个位置旋转到另一个位置所形成的图形。顶点始边终边oAB定义2:生活实例 逆时针 顺时针拧松拧紧生活实例三、合作探究(1)
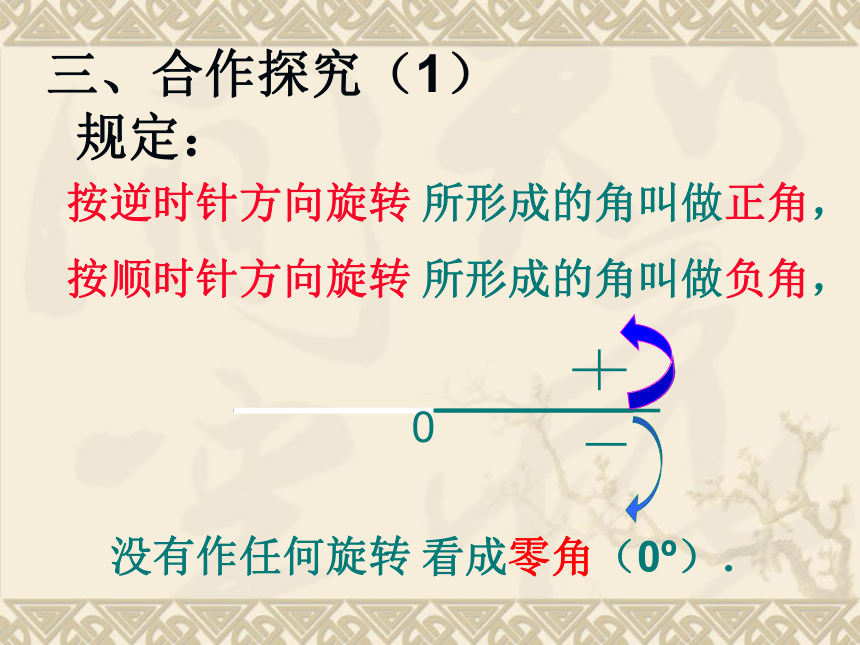
规定:按逆时针方向旋转按顺时针方向旋转所形成的角叫做正角,所形成的角叫做负角,看成零角(0o).0没有作任何旋转ABo390 oAoB450 o两个图形例子:思考:你的手表慢了5分钟,你是怎样将它校准的?假如你的手表快了1.5小时,你如何将它校准?当时间校准以后,分针转了多少度? -30°,540°⑶角的概念经过推广后,已包括正
角、负角和零角.⑴在不引起混淆的情况下,“角? ”
或“∠? ”可以简化成“? ”;⑵零角的终边与始边重合,如果?
是零角? = 0°;注意思考: ,那么
思考: 在不用量角器的条件下能比较这两角的大小吗?如何比较?合作探究(2):xyo 1)置角的顶点于原点角的终边(除端点外)落在第几象限就是第几象限角2)始边重合于X轴的非负半轴终边 象限角的概念:如果角的终边在坐标轴上, 就认为这个角不属于任何象限.那么下列各角:-45°,405°,210°,
-200°分别是第几象限的角? 思考1:在坐标系中画出-45°,-405°,
-765°, 315°并思考分别是第几象限的角?这些角有什么内在联系?-45°-405°315°合作探究三: S={β|β=α+k·360°,k∈Z}, 即任一与α终边相同的角,都可以表示成角α与整数个周角的和. 思考2:一般地,所有与角α终边相同的角,连同角α在内所构成的集合S可以表示成: 2、?是任一角;4、终边相同的角不一定相等,但相等的角终边一定相同.终边相同的有无限个,它们相差360°的整数倍;1、 k∈Z;注意 3、 k·360o与?之间是“+”号,如k·360o-30o,应看成k·360o+(-30o); 例1 在0°~360°范围内,找出与950 °角终边相同的角,并判定它是第几象限角. 所以,在0°~360°范围内与 950 °角终边相同的角是230 °,是第三象限角.解:950 °=230°+2X360°下一页-950° 变:写出与600角终边相同角的集合S,
并把S中适合不等式-3600≤β<7200的
元素β写出来.解 S ={β| β=600+K?3600,K∈Z}S 中适合-3600≤β<7200的元素是:600-1x3600=-3000600+0x3600=600600+1x3600=4200下一页例2 写出终边落在y轴上的角的集合。S=S1∪S2终边落在y轴上的角的集合为={β| β=900+1800 的偶数倍}∪{β| β=900+1800 的奇数倍}={β| β=900+1800 的整数倍} ={β| β=900+K?1800 ,K∈Z}{偶数}∪{奇数}={整数}给你留下印象最深的是什么?通过这堂课,你学到了什么?你还有一些什么想法?课堂小结课堂小结:1.角的
分类正角:射线按逆时针方向旋转形成的角负角:射线按顺时针方向旋转形成的角零角:射线不作旋转形成的角1)置角的顶点于原点2)始边重合于X轴的非负半轴2.象限角终边落在第几象限就是第几象限角3 . 终边与 角α相同的角的集合S={β|β=α+k·360°,k∈Z}作业布置:1、基本作业:P5练习3,练习42、拓展作业:3、学习小组研究课题:初中我们研究了锐角的三角函数,今天角的概念推广后,三角函数需要推广吗?如何推广?小组研究后以小论文的形式在班级交流!参考练习 (1)与-496°终边相同的角是 ,
它是第 象限的角,它们中最小正角是 ,
最大负角是 。 (2)时针经过3小时20分,则时针转过的
角度为 ,分针转过的角度为 。 -496°+k·360°(k∈Z) 三 240° —136° -100° -1200° (3)若α、β的终边关于x轴对称,则α与β的关系是 ;若α与β的终边关于y轴对称,则α与β的关系是 ;若α、β的终边关于原点对称,则α与β的关系是 ;若角α是第二象限角,则180°-α是第 象限角。 α十β=k·360°(k∈Z) α十β=180°十k·360。(k∈Z) α一β=180°十k·360°(k∈Z) 一 所以,在0°~360°范围内与- 950 °角终边相同的角是130 °,是第二象限角.解:-950 °=130°-3X360°返回
规定:按逆时针方向旋转按顺时针方向旋转所形成的角叫做正角,所形成的角叫做负角,看成零角(0o).0没有作任何旋转ABo390 oAoB450 o两个图形例子:思考:你的手表慢了5分钟,你是怎样将它校准的?假如你的手表快了1.5小时,你如何将它校准?当时间校准以后,分针转了多少度? -30°,540°⑶角的概念经过推广后,已包括正
角、负角和零角.⑴在不引起混淆的情况下,“角? ”
或“∠? ”可以简化成“? ”;⑵零角的终边与始边重合,如果?
是零角? = 0°;注意思考: ,那么
思考: 在不用量角器的条件下能比较这两角的大小吗?如何比较?合作探究(2):xyo 1)置角的顶点于原点角的终边(除端点外)落在第几象限就是第几象限角2)始边重合于X轴的非负半轴终边 象限角的概念:如果角的终边在坐标轴上, 就认为这个角不属于任何象限.那么下列各角:-45°,405°,210°,
-200°分别是第几象限的角? 思考1:在坐标系中画出-45°,-405°,
-765°, 315°并思考分别是第几象限的角?这些角有什么内在联系?-45°-405°315°合作探究三: S={β|β=α+k·360°,k∈Z}, 即任一与α终边相同的角,都可以表示成角α与整数个周角的和. 思考2:一般地,所有与角α终边相同的角,连同角α在内所构成的集合S可以表示成: 2、?是任一角;4、终边相同的角不一定相等,但相等的角终边一定相同.终边相同的有无限个,它们相差360°的整数倍;1、 k∈Z;注意 3、 k·360o与?之间是“+”号,如k·360o-30o,应看成k·360o+(-30o); 例1 在0°~360°范围内,找出与950 °角终边相同的角,并判定它是第几象限角. 所以,在0°~360°范围内与 950 °角终边相同的角是230 °,是第三象限角.解:950 °=230°+2X360°下一页-950° 变:写出与600角终边相同角的集合S,
并把S中适合不等式-3600≤β<7200的
元素β写出来.解 S ={β| β=600+K?3600,K∈Z}S 中适合-3600≤β<7200的元素是:600-1x3600=-3000600+0x3600=600600+1x3600=4200下一页例2 写出终边落在y轴上的角的集合。S=S1∪S2终边落在y轴上的角的集合为={β| β=900+1800 的偶数倍}∪{β| β=900+1800 的奇数倍}={β| β=900+1800 的整数倍} ={β| β=900+K?1800 ,K∈Z}{偶数}∪{奇数}={整数}给你留下印象最深的是什么?通过这堂课,你学到了什么?你还有一些什么想法?课堂小结课堂小结:1.角的
分类正角:射线按逆时针方向旋转形成的角负角:射线按顺时针方向旋转形成的角零角:射线不作旋转形成的角1)置角的顶点于原点2)始边重合于X轴的非负半轴2.象限角终边落在第几象限就是第几象限角3 . 终边与 角α相同的角的集合S={β|β=α+k·360°,k∈Z}作业布置:1、基本作业:P5练习3,练习42、拓展作业:3、学习小组研究课题:初中我们研究了锐角的三角函数,今天角的概念推广后,三角函数需要推广吗?如何推广?小组研究后以小论文的形式在班级交流!参考练习 (1)与-496°终边相同的角是 ,
它是第 象限的角,它们中最小正角是 ,
最大负角是 。 (2)时针经过3小时20分,则时针转过的
角度为 ,分针转过的角度为 。 -496°+k·360°(k∈Z) 三 240° —136° -100° -1200° (3)若α、β的终边关于x轴对称,则α与β的关系是 ;若α与β的终边关于y轴对称,则α与β的关系是 ;若α、β的终边关于原点对称,则α与β的关系是 ;若角α是第二象限角,则180°-α是第 象限角。 α十β=k·360°(k∈Z) α十β=180°十k·360。(k∈Z) α一β=180°十k·360°(k∈Z) 一 所以,在0°~360°范围内与- 950 °角终边相同的角是130 °,是第二象限角.解:-950 °=130°-3X360°返回
