3.1数乘向量 课件(25张PPT)
文档属性
| 名称 | 3.1数乘向量 课件(25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 580.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-20 00:00:00 | ||
图片预览






文档简介
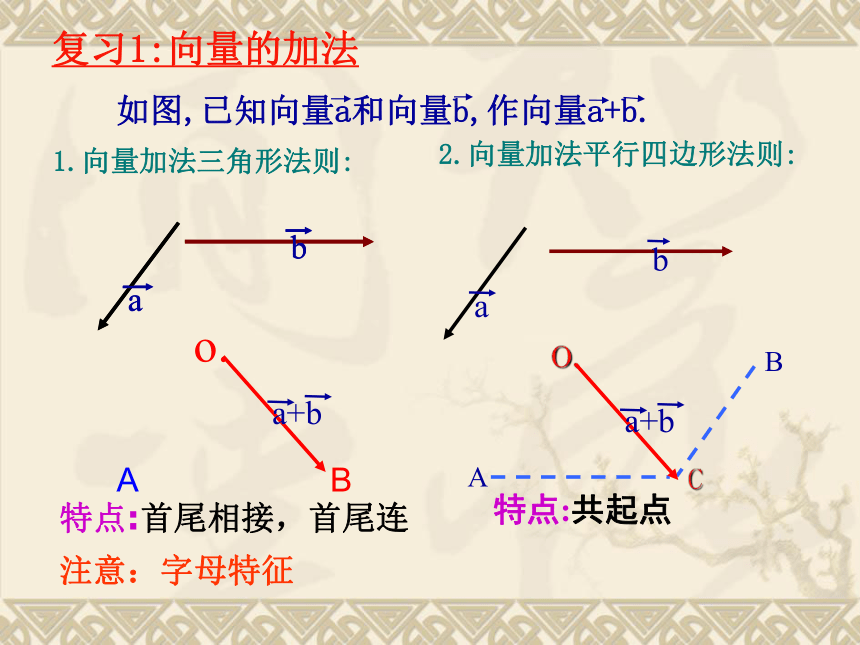
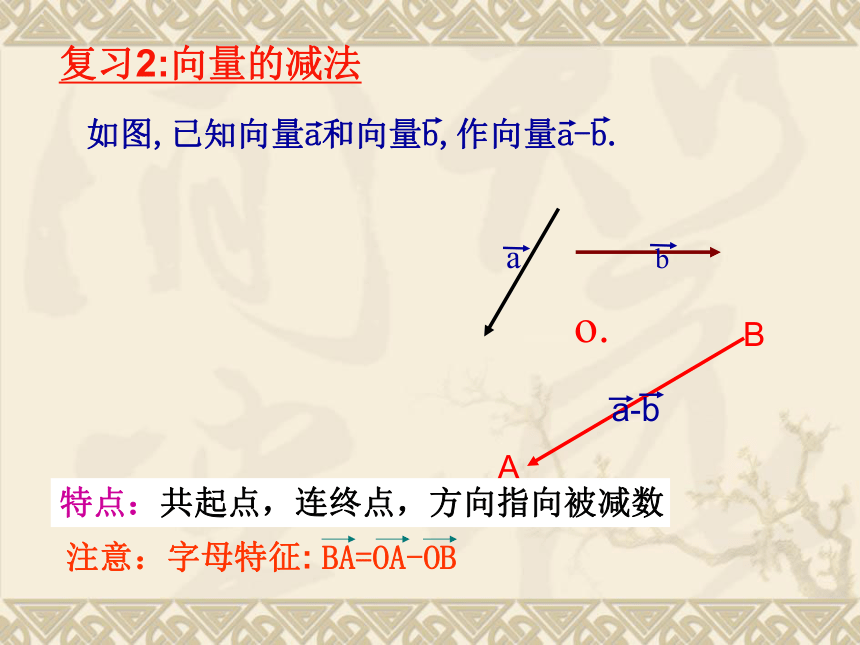
课件25张PPT。复习1:向量的加法BAo.O.AB1.向量加法三角形法则:2.向量加法平行四边形法则:特点:首尾相接,首尾连特点:共起点注意:字母特征复习2:向量的减法o.BA特点:共起点,连终点,方向指向被减数实际背景这两个向量之间有什么关系?向量 |λ||a| 相同 相反 几何意义?把一个向量沿着它的方向或反方向延长或缩短思考 向量加法的运算律: 探究:数乘向量的运算律?交换律:a+b=________.
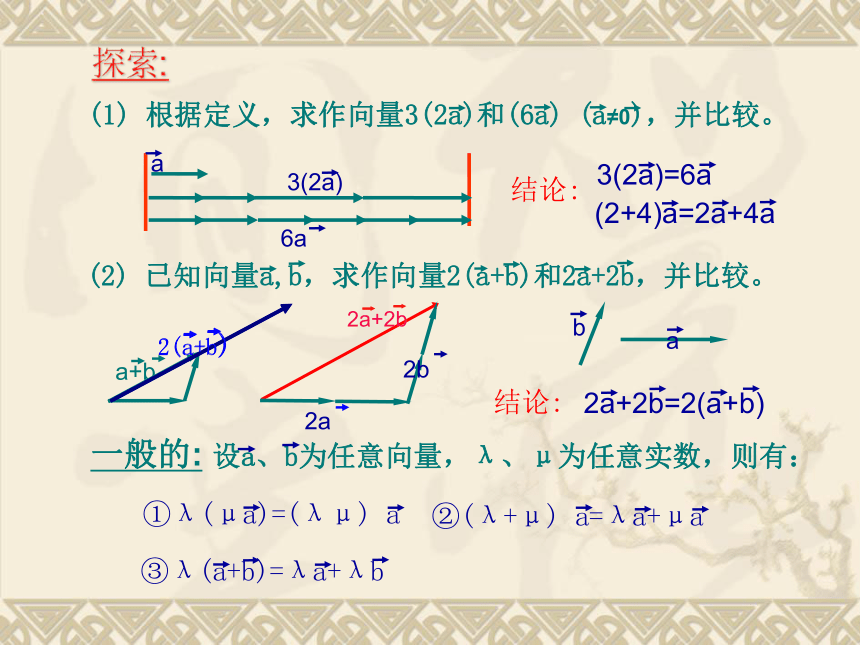
结合律:(a+b)+c=a+(________).探索:aλ a+μ a λμ a λ a+λ b 应用:探究:非零 λ 非零 λ 共线向量定理 【例1】计算(口答):
【变式1】若 化简
的结果为( )
【解析】选A.例2:解: 【变式2】
A,B,C是平面内的三点,且A与B不重合,O是平面内任意一点.证明:若点C在直线AB上,则存在实数λ,使得 OC=λOA+(1-λ)OB。反之,也成立。【练习】设 是不共线的向量,已知向量
若A,B,D三点共线,求k的值.
【解题提示】证明存在实数λ,使得
【解析】
假设存在实数λ使
∴
得
∴k=-8.【练习】设两个非零向量 与 不共线.
(1)若
求证:A、B、D三点共线.
(2)试确定实数k,使 和 共线.【规范解答】
共线 又 有公共点B,
∴A、B、D三点共线. (2) 和 共线,则存在实数λ,使得
即
∵非零向量 与 不共线,
∴k-λ=0且1-λk=0,
∴k=±1. 本题延拓:小结回顾:作业:教材87页A组1.2.4【思考】如图,在△ABC中,D、E
为边AB的两个三等分点,
求
【审题指导】由D、E为边AB的两个三等分点可知A、B、D、
E四点共线,从而向量 均可以由向量 表示,而向
量 可由向量 表示,从而问题可解.探究:
结合律:(a+b)+c=a+(________).探索:aλ a+μ a λμ a λ a+λ b 应用:探究:非零 λ 非零 λ 共线向量定理 【例1】计算(口答):
【变式1】若 化简
的结果为( )
【解析】选A.例2:解: 【变式2】
A,B,C是平面内的三点,且A与B不重合,O是平面内任意一点.证明:若点C在直线AB上,则存在实数λ,使得 OC=λOA+(1-λ)OB。反之,也成立。【练习】设 是不共线的向量,已知向量
若A,B,D三点共线,求k的值.
【解题提示】证明存在实数λ,使得
【解析】
假设存在实数λ使
∴
得
∴k=-8.【练习】设两个非零向量 与 不共线.
(1)若
求证:A、B、D三点共线.
(2)试确定实数k,使 和 共线.【规范解答】
共线 又 有公共点B,
∴A、B、D三点共线. (2) 和 共线,则存在实数λ,使得
即
∵非零向量 与 不共线,
∴k-λ=0且1-λk=0,
∴k=±1. 本题延拓:小结回顾:作业:教材87页A组1.2.4【思考】如图,在△ABC中,D、E
为边AB的两个三等分点,
求
【审题指导】由D、E为边AB的两个三等分点可知A、B、D、
E四点共线,从而向量 均可以由向量 表示,而向
量 可由向量 表示,从而问题可解.探究:
