3.2平面向量基本定理 课件(30张PPT)
文档属性
| 名称 | 3.2平面向量基本定理 课件(30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-20 00:00:00 | ||
图片预览










文档简介
课件30张PPT。§3.2平面向量基本定理
实 例 1导弹的飞行图片,如何求导弹此时竖直和水平方向速度?实 例 2
力的分解任务一:①是不是每一个向量都可以分解成两个不共线向量?且分解是唯一?
②对于平面上两个不共线向量 ,是不是平面上的所有向量都可以用它们来表示?
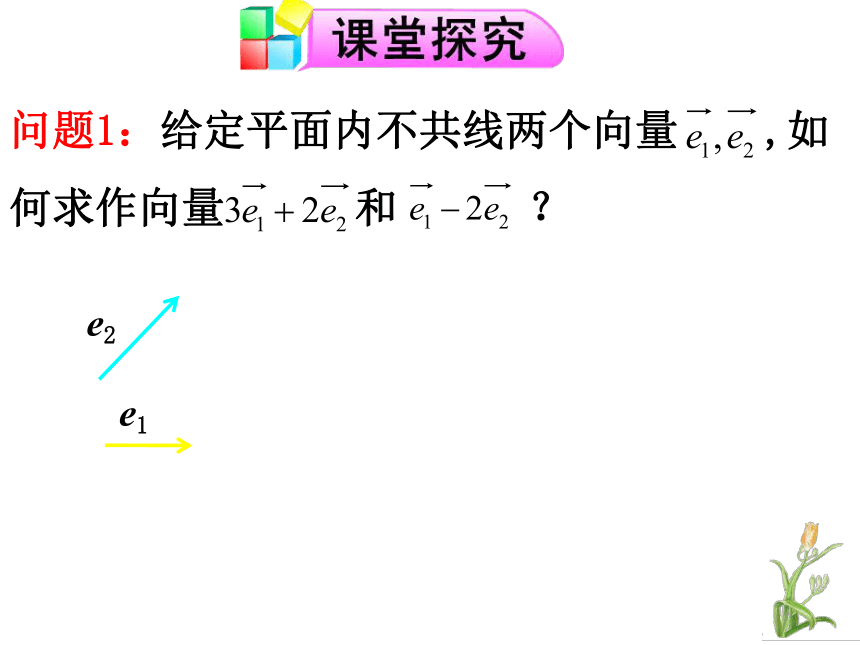
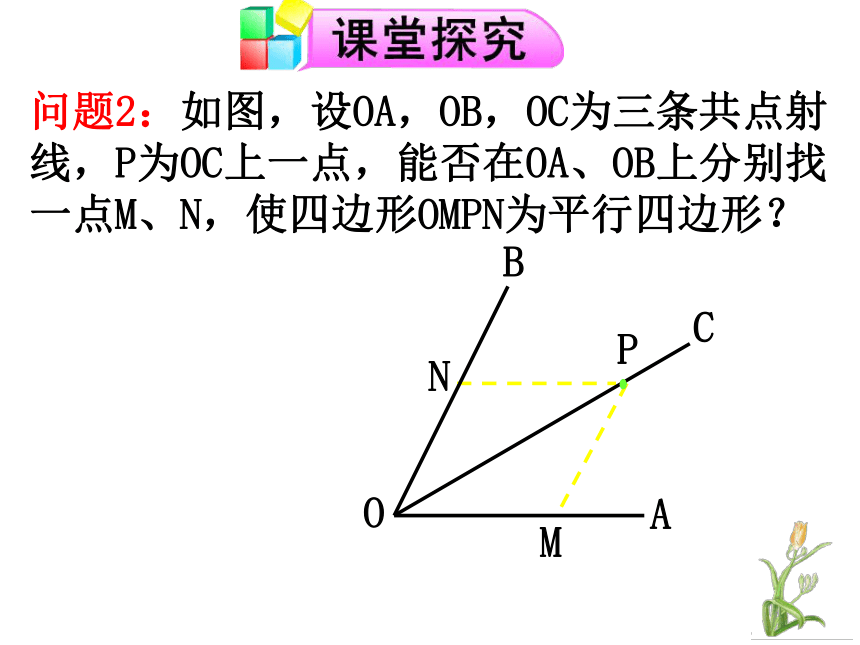
预备知识问题1:给定平面内不共线两个向量 ,如何求作向量 和 ? 问题2:如图,设OA,OB,OC为三条共点射线,P为OC上一点,能否在OA、OB上分别找一点M、N,使四边形OMPN为平行四边形?问题3:在下列两图中,向量
不共线,能否在直线OA、OB上分别找一点M、N,使 ?问题4:问题5:问题6:根据上述分析,平面内任一向量 都可以由这个平面内两个不共线的向量
表示出来,从而可形成一个定理.你能完整地描述这个定理的内容吗?若 是同一平面内的两个不共线向量,则对于这一平面内的任意向量 ,有且只有一对实数λ1,λ2,使 .问题7:上述定理称为平面向量基本定理,不共线向量e1,e2叫做表示这一平面内所有向量的一组基底. 那么同一平面内可以作基底的向量有多少组?不同基底对应向量a的表示式是否相同?问题8:在平面向量基本定理中,为什么要求向量 不共线? 可以作为基底吗?问题9:若向量a与e1或e2共线,a还能用λ1e1+λ2e2表示吗?a=λ1e1+0e2a=0e1+λ2e2问题10:若定理中的 ,能被基底
分解吗?任务一总结:平面向量基本定理
若 是同一平面内的两个不共线向量,则对于这一平面内的任意向量 ,有且只有一对实数λ1,λ2,使 .强调:任务二:定理运用训练1.判断正误.(正确的打“√”,错误的打“×”)
(1)一个平面内只有一对不共线的向量可作为表示该平面内所有向量的基底.( )
(2)若e1,e2是同一平面内两个不共线向量,则λ1e1+λ2e2
(λ1,λ2为实数)可以表示该平面内所有向量.( )
(3)若ae1+be2=ce1+de2(a,b,c,d∈R),则a=c,b=d.( )
√××3★例1.在平行四边形ABCD中,E,F分别是BC,DC的中点, 用 表示试一试:若 用 表示
★★1、提问:通过本节学习,你有哪些收获?2、在学生回答的基础上,概括如下:
(1)一条定理
(2)关注基底
(3)简单应用
不用相当的独立功夫,不论在哪个严重的问题上都不能找出真理;谁怕用功夫,谁就无法找到真理.
——列宁感 谢 指 导
实 例 1导弹的飞行图片,如何求导弹此时竖直和水平方向速度?实 例 2
力的分解任务一:①是不是每一个向量都可以分解成两个不共线向量?且分解是唯一?
②对于平面上两个不共线向量 ,是不是平面上的所有向量都可以用它们来表示?
预备知识问题1:给定平面内不共线两个向量 ,如何求作向量 和 ? 问题2:如图,设OA,OB,OC为三条共点射线,P为OC上一点,能否在OA、OB上分别找一点M、N,使四边形OMPN为平行四边形?问题3:在下列两图中,向量
不共线,能否在直线OA、OB上分别找一点M、N,使 ?问题4:问题5:问题6:根据上述分析,平面内任一向量 都可以由这个平面内两个不共线的向量
表示出来,从而可形成一个定理.你能完整地描述这个定理的内容吗?若 是同一平面内的两个不共线向量,则对于这一平面内的任意向量 ,有且只有一对实数λ1,λ2,使 .问题7:上述定理称为平面向量基本定理,不共线向量e1,e2叫做表示这一平面内所有向量的一组基底. 那么同一平面内可以作基底的向量有多少组?不同基底对应向量a的表示式是否相同?问题8:在平面向量基本定理中,为什么要求向量 不共线? 可以作为基底吗?问题9:若向量a与e1或e2共线,a还能用λ1e1+λ2e2表示吗?a=λ1e1+0e2a=0e1+λ2e2问题10:若定理中的 ,能被基底
分解吗?任务一总结:平面向量基本定理
若 是同一平面内的两个不共线向量,则对于这一平面内的任意向量 ,有且只有一对实数λ1,λ2,使 .强调:任务二:定理运用训练1.判断正误.(正确的打“√”,错误的打“×”)
(1)一个平面内只有一对不共线的向量可作为表示该平面内所有向量的基底.( )
(2)若e1,e2是同一平面内两个不共线向量,则λ1e1+λ2e2
(λ1,λ2为实数)可以表示该平面内所有向量.( )
(3)若ae1+be2=ce1+de2(a,b,c,d∈R),则a=c,b=d.( )
√××3★例1.在平行四边形ABCD中,E,F分别是BC,DC的中点, 用 表示试一试:若 用 表示
★★1、提问:通过本节学习,你有哪些收获?2、在学生回答的基础上,概括如下:
(1)一条定理
(2)关注基底
(3)简单应用
不用相当的独立功夫,不论在哪个严重的问题上都不能找出真理;谁怕用功夫,谁就无法找到真理.
——列宁感 谢 指 导
