4.3单位圆与诱导公式 课件(17张PPT)
文档属性
| 名称 | 4.3单位圆与诱导公式 课件(17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 230.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-20 22:47:58 | ||
图片预览






文档简介
课件17张PPT。课题:三角函数中的化简求值教材版本:北师大版学生年级:高一教学过程:一、知识要点
1.学生默写特殊角的三角函数值
2.任意角α的三角函数定义:在角α的终边上任取一点(不同于原点)M(x,y)
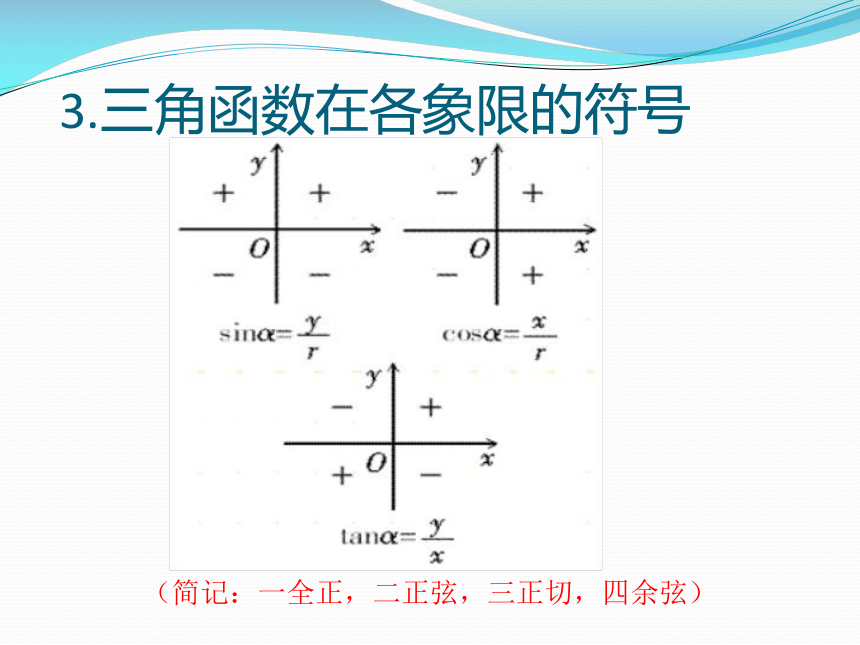
3.三角函数在各象限的符号
(简记:一全正,二正弦,三正切,四余弦)绕着横轴(x)偏转(四个象限)
(1) sin(2kπ+α)=sin α,
cos(2kπ+α)=cos α,
tan(2kπ+α)=tan α;
(2) sin(π- α)= sin α,
cos(π- α)=- cos α,
tan(π- α)=- tan α;
(3) sin(π+ α)= -sin α,
cos(π+ α)=- cos α,
tan(π+ α)= tan α;
(4) sin(- α)=- sin α,
cos(- α)=cos α,
tan(- α)=-tan α. xyo2kπ+απ-απ+α2kπ-α(或-α)4.诱导公式(1)sin(π/2-α)=cosα ,
cos(π/2-α)=sinα
tan(π/2-α)=cotα ;
(2) sin(π/2+α)=cosα ,
cos(π/2+α)=-sinα
tan(π/2+α)=-cotα;
(3)sin(3π/2-α)=-cosα ,
cos(3π/2-α)=-sinα
tan(3π/2-α)=cotα;
(4)sin(3π/2+α)=-cosα,
cos(3π/2+α)=sinα
tan(3π/2+α)=-cotα.绕着纵轴(y)偏转(四个象限)xyoπ/2-απ/2+α3π/2-α3π/2+α绕着横轴(x)偏转(四个象限)
(1) sin(2kπ+α)=sin α, cos(2kπ+α)=cos α, tan(2kπ+α)=tan α;
(2) sin(π- α)= sin α, cos(π- α)=- cos α, tan(π- α)=- tan α;
(3) sin(π+ α)= -sin α, cos(π+ α)=- cos α, tan(π+ α)= tan α;
(4) sin(- α)=- sin α, cos(- α)=cos α, tan(- α)=-tan α.
绕着纵轴(y)偏转(四个象限)
(1)sin(π/2-α)=cosα , cos(π/2-α)=sinα , tan(π/2-α)=cotα ;
(2) sin(π/2+α)=cosα , cos(π/2+α)=-sinα, tan(π/2+α)=-cotα;
(3)sin(3π/2-α)=-cosα , cos(3π/2-α)=-sinα, tan(3π/2-α)=cotα;
(4)sin(3π/2+α)=-cosα, cos(3π/2+α)=sinα , tan(3π/2+α)=-cotα.
诱导公式记忆法:α当锐角看,函数名纵变横不变,符号看象限。 5.同角三角函数间的基本关系二 、举例例1.求值
例2求值学生练习 1.求值2.求值<0三、小结1利用诱导公式化简求值的方法是:
化负为正——化大为小——小到锐角再停止
2学生应该灵活使用诱导公式,不可以死记硬背,理解每组诱导公式的实质,在解题过程中灵活转化。四、作业1.求值
2.已知角α终边上一点 , 求cosα和 tan(π+α)的值。五、板书设计1知识要点:复习有关概念
2例题讲解
3学生练习
4小结
5作业
1.学生默写特殊角的三角函数值
2.任意角α的三角函数定义:在角α的终边上任取一点(不同于原点)M(x,y)
3.三角函数在各象限的符号
(简记:一全正,二正弦,三正切,四余弦)绕着横轴(x)偏转(四个象限)
(1) sin(2kπ+α)=sin α,
cos(2kπ+α)=cos α,
tan(2kπ+α)=tan α;
(2) sin(π- α)= sin α,
cos(π- α)=- cos α,
tan(π- α)=- tan α;
(3) sin(π+ α)= -sin α,
cos(π+ α)=- cos α,
tan(π+ α)= tan α;
(4) sin(- α)=- sin α,
cos(- α)=cos α,
tan(- α)=-tan α. xyo2kπ+απ-απ+α2kπ-α(或-α)4.诱导公式(1)sin(π/2-α)=cosα ,
cos(π/2-α)=sinα
tan(π/2-α)=cotα ;
(2) sin(π/2+α)=cosα ,
cos(π/2+α)=-sinα
tan(π/2+α)=-cotα;
(3)sin(3π/2-α)=-cosα ,
cos(3π/2-α)=-sinα
tan(3π/2-α)=cotα;
(4)sin(3π/2+α)=-cosα,
cos(3π/2+α)=sinα
tan(3π/2+α)=-cotα.绕着纵轴(y)偏转(四个象限)xyoπ/2-απ/2+α3π/2-α3π/2+α绕着横轴(x)偏转(四个象限)
(1) sin(2kπ+α)=sin α, cos(2kπ+α)=cos α, tan(2kπ+α)=tan α;
(2) sin(π- α)= sin α, cos(π- α)=- cos α, tan(π- α)=- tan α;
(3) sin(π+ α)= -sin α, cos(π+ α)=- cos α, tan(π+ α)= tan α;
(4) sin(- α)=- sin α, cos(- α)=cos α, tan(- α)=-tan α.
绕着纵轴(y)偏转(四个象限)
(1)sin(π/2-α)=cosα , cos(π/2-α)=sinα , tan(π/2-α)=cotα ;
(2) sin(π/2+α)=cosα , cos(π/2+α)=-sinα, tan(π/2+α)=-cotα;
(3)sin(3π/2-α)=-cosα , cos(3π/2-α)=-sinα, tan(3π/2-α)=cotα;
(4)sin(3π/2+α)=-cosα, cos(3π/2+α)=sinα , tan(3π/2+α)=-cotα.
诱导公式记忆法:α当锐角看,函数名纵变横不变,符号看象限。 5.同角三角函数间的基本关系二 、举例例1.求值
例2求值学生练习 1.求值2.求值<0三、小结1利用诱导公式化简求值的方法是:
化负为正——化大为小——小到锐角再停止
2学生应该灵活使用诱导公式,不可以死记硬背,理解每组诱导公式的实质,在解题过程中灵活转化。四、作业1.求值
2.已知角α终边上一点 , 求cosα和 tan(π+α)的值。五、板书设计1知识要点:复习有关概念
2例题讲解
3学生练习
4小结
5作业
