5 从力做的功到向量的数量积 课件(19张PPT)
文档属性
| 名称 | 5 从力做的功到向量的数量积 课件(19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-20 00:00:00 | ||
图片预览




文档简介
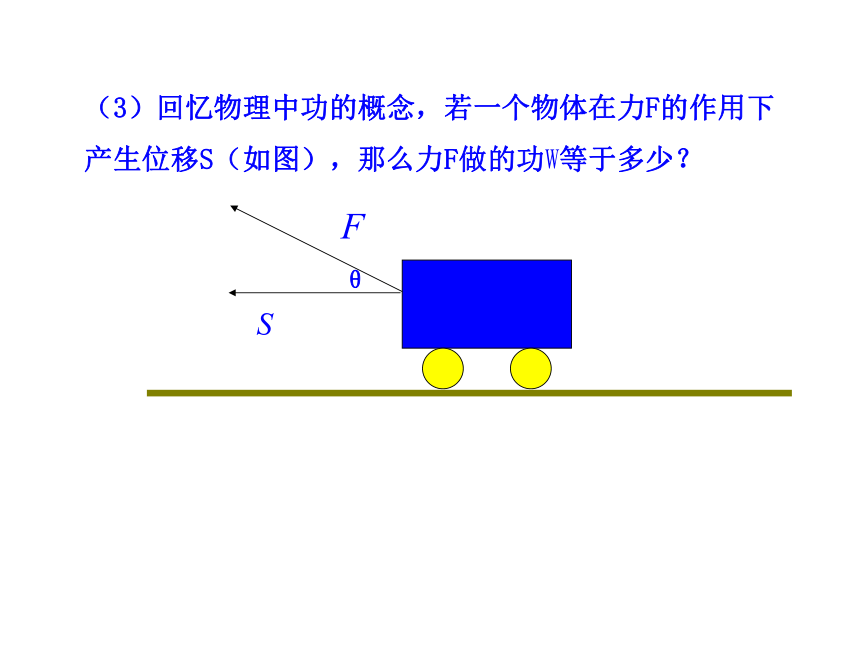
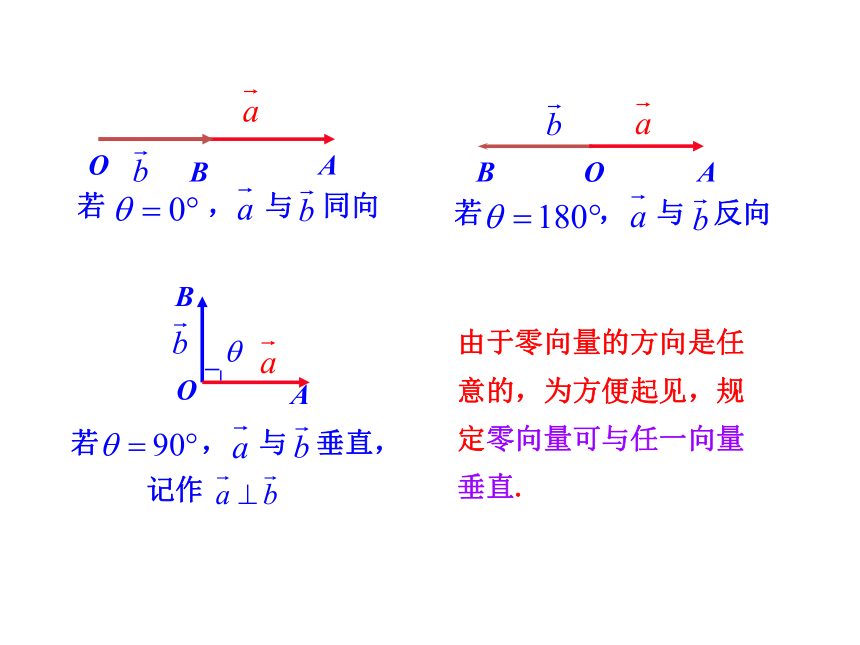
课件19张PPT。§5 从力做的功到向量的数量积(1)请同学们回顾,我们已经研究了向量的哪些运算?其运算结果是什么?(2)我们是怎样引入向量加法的运算的?请回忆下当时的研究思路?物理模型→概念→性质→运算律→应用(3)回忆物理中功的概念,若一个物体在力F的作用下产生位移S(如图),那么力F做的功W等于多少? θ(4)这个公式有什么特点?结合向量的学习你有什么想法?①W(功)是_量④ θ是_③S (位移)是_量 ②F(力)是_ 量成果1 向量的夹角数量积的定义由于零向量的方向是任意的,为方便起见,规定零向量可与任一向量垂直.成果2 平面向量的数量积的定义
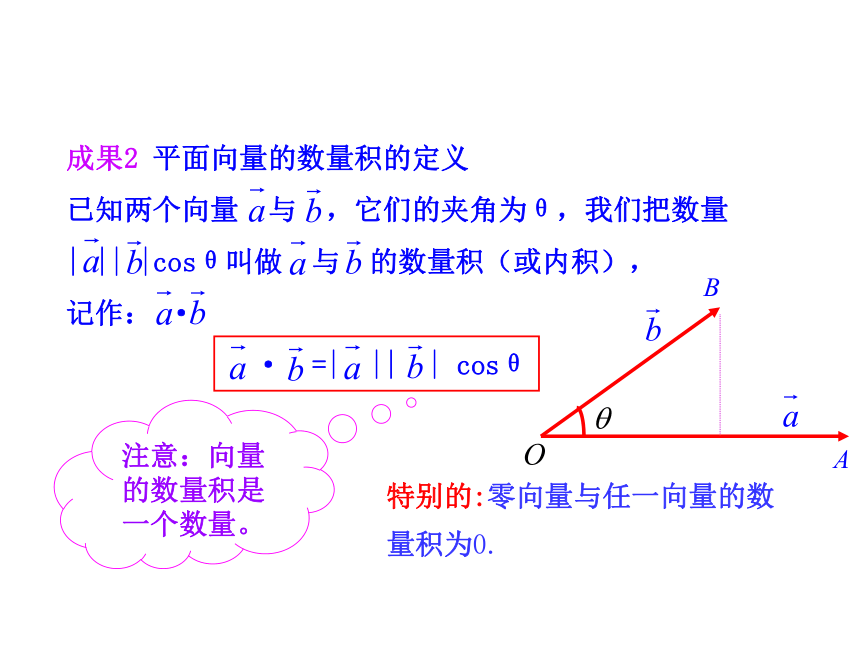
已知两个向量 与 ,它们的夹角为θ,我们把数量
| || |cosθ叫做 与 的数量积(或内积),
记作: ·
· =| || | cosθ 注意:向量的数量积是一个数量。特别的:零向量与任一向量的数量积为0.>0成果3 向量的射影?数量积的几何意义<0=0OBAB1物理实例中,分力 的大小︱ ︱cosθ,
其是力 在位移 方向上的射影。θFSF2F1成果4 数量积的几何意义数量积的常用性质数量积的常用性质数量积的常用性质数量积的常用性质(4)向量数量积运算中出现了向量的夹角,思考下如何求向量夹角呢?【成果5 重要性质】
1.若 是单位向量,则
2.
3.
4.
5.
当且仅当 ∥ 时等号成立. 反之成立吗?解答:不成立.解答:成立.数量积的运算律类比实数乘法的运算律,猜想向量数量积满足哪些运算律?小试牛刀本节课主要学习了:
(1)向量数量积的定义;
(2)向量数量积的几何意义;
(3)数量积的常用性质;
(4)向量的数量积的运算律.
已知两个向量 与 ,它们的夹角为θ,我们把数量
| || |cosθ叫做 与 的数量积(或内积),
记作: ·
· =| || | cosθ 注意:向量的数量积是一个数量。特别的:零向量与任一向量的数量积为0.>0成果3 向量的射影?数量积的几何意义<0=0OBAB1物理实例中,分力 的大小︱ ︱cosθ,
其是力 在位移 方向上的射影。θFSF2F1成果4 数量积的几何意义数量积的常用性质数量积的常用性质数量积的常用性质数量积的常用性质(4)向量数量积运算中出现了向量的夹角,思考下如何求向量夹角呢?【成果5 重要性质】
1.若 是单位向量,则
2.
3.
4.
5.
当且仅当 ∥ 时等号成立. 反之成立吗?解答:不成立.解答:成立.数量积的运算律类比实数乘法的运算律,猜想向量数量积满足哪些运算律?小试牛刀本节课主要学习了:
(1)向量数量积的定义;
(2)向量数量积的几何意义;
(3)数量积的常用性质;
(4)向量的数量积的运算律.
