必修4 第二章平面向量 从力做的功到向量的数量积 课件(21张PPT)
文档属性
| 名称 | 必修4 第二章平面向量 从力做的功到向量的数量积 课件(21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 543.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-20 00:00:00 | ||
图片预览








文档简介
课件21张PPT。从力做的功到向量的数量积从力做的功到向量的数量积
我们已学过数量的那些运算?问 题:如图:一个物体在力F =20N的作用下,向右水平移动了3m,求F所做的功?导 入
从力做的功到向量的数量积W=F·S=|F|·|S|cos?夹 角推进新知(夹角)
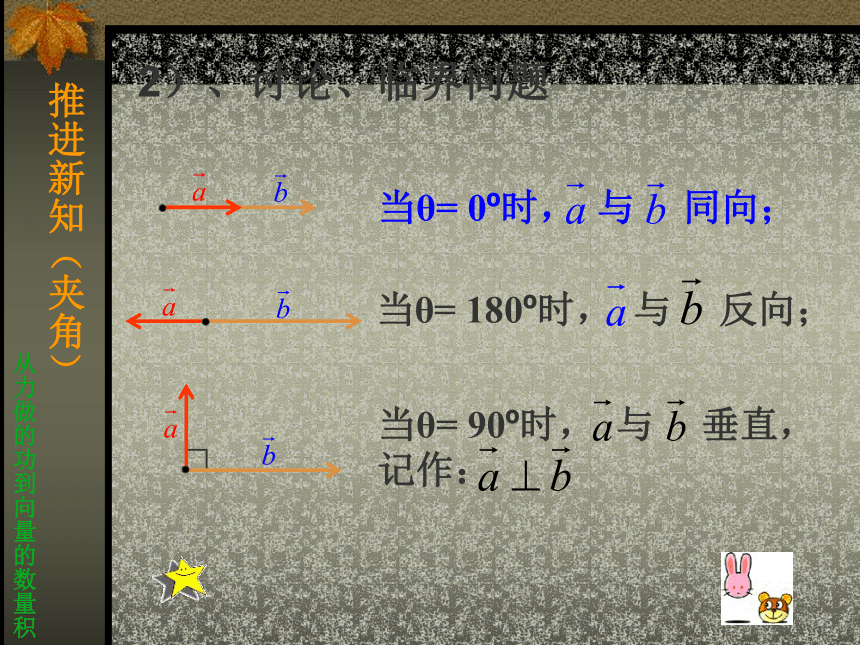
从力做的功到向量的数量积1)、定义2)、讨论、临界问题推进新知(夹角)
从力做的功到向量的数量积练 习在 中已知A=40°,B=25°,C=115°求下列向量的夹角:
(1) 的夹角。(2) 的夹角。
(3) 的夹角。推进新知(夹角)
从力做的功到向量的数量积射 影如图: 叫作向量 在 方向上的投影(射影)。新知理解(射影)
从力做的功到向量的数量积投影是个实数,可正、可负、可以为零。C探讨:由上述定义,猜想射影在什么时候为正?为负?为零?新知理解(射影)
从力做的功到向量的数量积平行长不变,倾斜长缩短,垂直成一点。结合余弦值的正负也能得出结论数量积1)、定义
已知非零向量 与 ,它们的夹角为 ? ,我们把数量 叫作 与 的数量积(或内积),记作 ,即规定探究新知(数量积)
从力做的功到向量的数量积2)、注意① 、 的结果是数量,正负如何确定?
当?为锐角时, >0
当?为钝角时, <0
当?=90°时, =0
当?=0°时, >0
当?=180°时, <0探究新知(数量积)
从力做的功到向量的数量积② 、 与 之间只能用·,不能改成其它任何一种符号。3)、几何意义新知理解
从力做的功到向量的数量积练 习(公式应用)新知巩固(练习)
从力做的功到向量的数量积练 习(公式应用)性质自主探究(性质)
从力做的功到向量的数量积例2:已知单位向量 , 的夹角为 ,求向量 , 的夹角。解:由单位向量 、 的夹角为 得小结1.向量的夹角及其范围
0o≤θ≤180o
2.向量的数量积的定义
作业:P97习题A4、5、6谢 谢!从力做的功到向量的数量积
亳州一中南校:葛 颂
我们已学过数量的那些运算?问 题:如图:一个物体在力F =20N的作用下,向右水平移动了3m,求F所做的功?导 入
从力做的功到向量的数量积W=F·S=|F|·|S|cos?夹 角推进新知(夹角)
从力做的功到向量的数量积1)、定义2)、讨论、临界问题推进新知(夹角)
从力做的功到向量的数量积练 习在 中已知A=40°,B=25°,C=115°求下列向量的夹角:
(1) 的夹角。(2) 的夹角。
(3) 的夹角。推进新知(夹角)
从力做的功到向量的数量积射 影如图: 叫作向量 在 方向上的投影(射影)。新知理解(射影)
从力做的功到向量的数量积投影是个实数,可正、可负、可以为零。C探讨:由上述定义,猜想射影在什么时候为正?为负?为零?新知理解(射影)
从力做的功到向量的数量积平行长不变,倾斜长缩短,垂直成一点。结合余弦值的正负也能得出结论数量积1)、定义
已知非零向量 与 ,它们的夹角为 ? ,我们把数量 叫作 与 的数量积(或内积),记作 ,即规定探究新知(数量积)
从力做的功到向量的数量积2)、注意① 、 的结果是数量,正负如何确定?
当?为锐角时, >0
当?为钝角时, <0
当?=90°时, =0
当?=0°时, >0
当?=180°时, <0探究新知(数量积)
从力做的功到向量的数量积② 、 与 之间只能用·,不能改成其它任何一种符号。3)、几何意义新知理解
从力做的功到向量的数量积练 习(公式应用)新知巩固(练习)
从力做的功到向量的数量积练 习(公式应用)性质自主探究(性质)
从力做的功到向量的数量积例2:已知单位向量 , 的夹角为 ,求向量 , 的夹角。解:由单位向量 、 的夹角为 得小结1.向量的夹角及其范围
0o≤θ≤180o
2.向量的数量积的定义
作业:P97习题A4、5、6谢 谢!从力做的功到向量的数量积
亳州一中南校:葛 颂
