6 余弦函数的图像和性质 课件(26张PPT)
文档属性
| 名称 | 6 余弦函数的图像和性质 课件(26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-20 22:45:09 | ||
图片预览




文档简介
课件26张PPT。课题:余弦函数的图像与性质
单位:太和二中
§6 余弦函数的图像与性质y1.会用“图像变换法”和“五点法”作余弦函数的图像.(重点)
2.掌握余弦函数y=cosx的图像和性质.(重点)
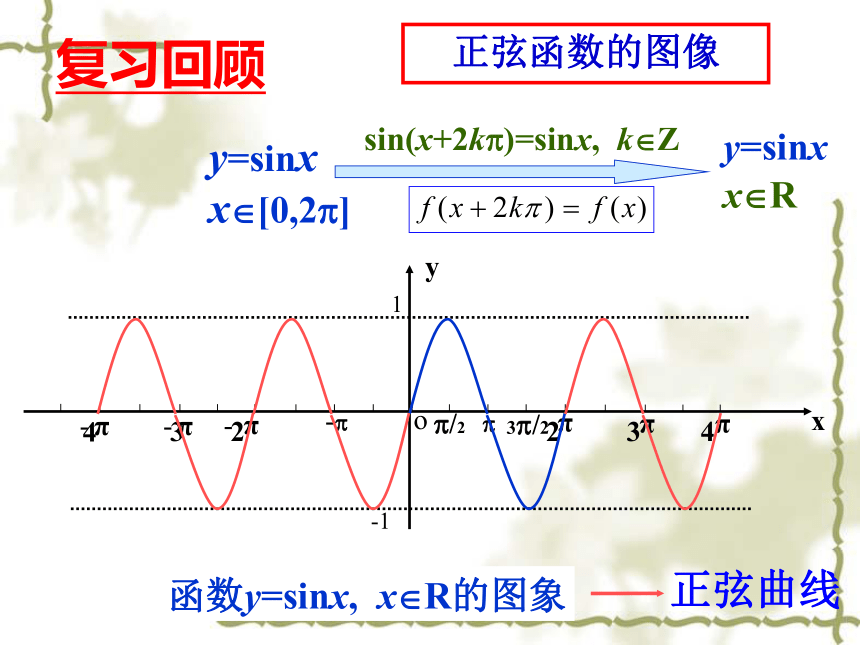
3.会应用余弦函数y=cosx的图像与性质解决一些简单问题.(难点)y=sinx x?[0,2?]y=sinx x?Rsin(x+2k?)=sinx, k?Z 正弦函数的图像函数y=sinx, x?R的图象正弦曲线复习回顾 余弦函数y=cosx (x∈R) 的图像 思考:如何将余弦函数用诱导公式写成正弦函数? 方法一(平移法):
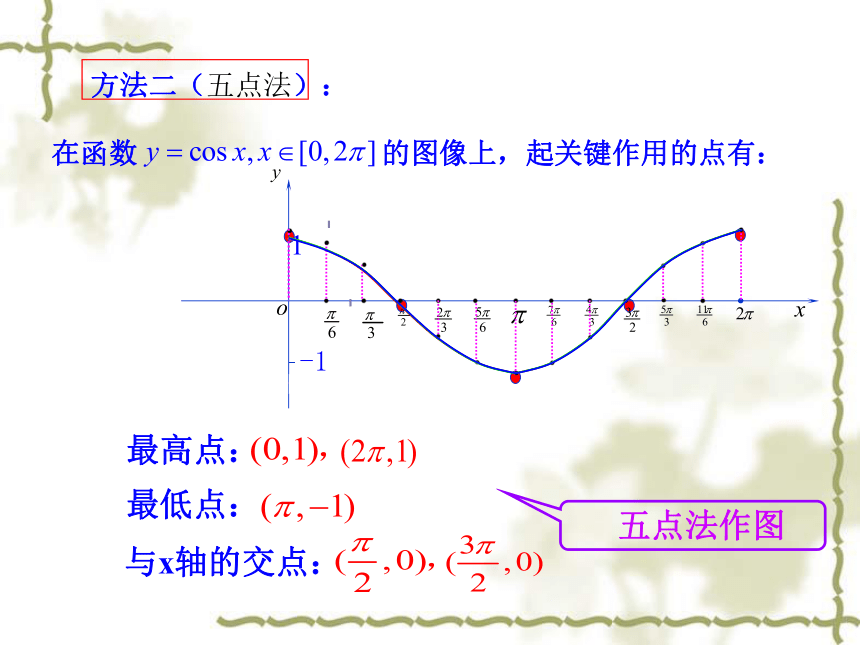
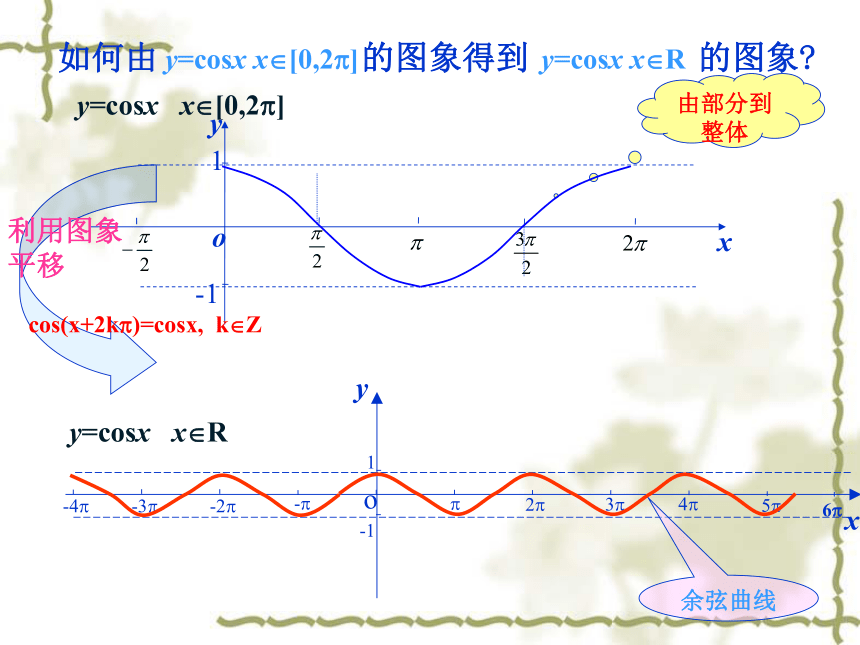
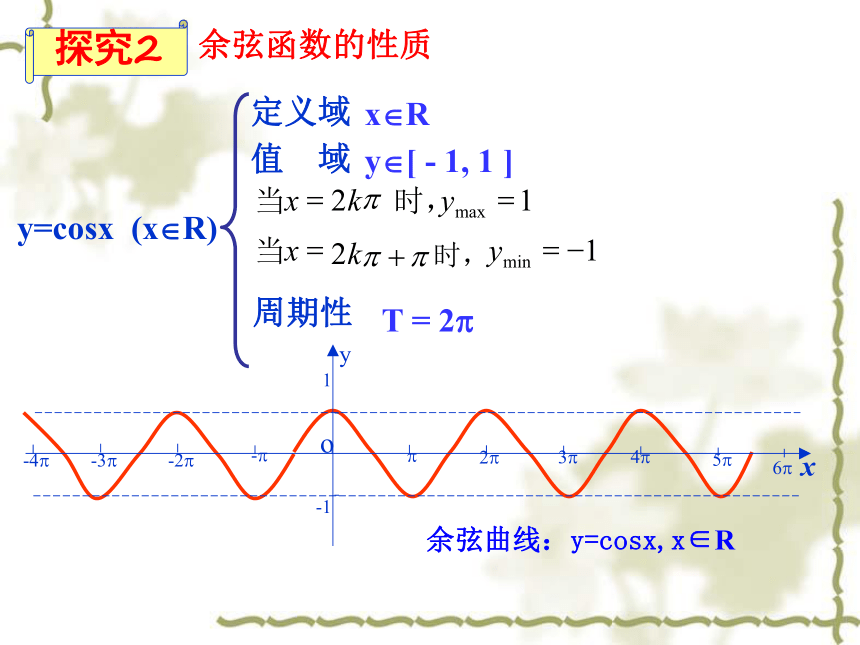
余弦曲线的图像可以通过将正弦曲线向左平移 个单位长度而得到.余弦函数的图像叫作余弦曲线.根据诱导公式,可得:课堂探究探究1余弦函数的图象 正弦函数的图象 余弦曲线正弦曲线形状完全一样只是位置不同由未知向已知转化方法:利用图像平移合作探究最高点:最低点:与x轴的交点:-1方法二(五点法):由部分到整体余弦曲线 y=cosx (x?R) 定义域值 域周期性x?Ry?[ - 1, 1 ]T = 2? 余弦函数的性质余弦曲线:y=cosx,x∈R探究2 余弦函数的单调性 y=cosx (x?R)的单调区间: 1 -1 -1cos(-x)= cosx (x?R) 余弦函数的奇偶性关于y轴对称x思考2:如何判断三角函数的奇偶性?
提示:(1)利用图像法:若图像关于原点对称,则函数为奇函数;若图像关于y轴对称,则函数为偶函数.
(2)根据奇偶性的定义判断:若对定义域内的任意x都有f(-x)=f(x),则函数为偶函数;若对定义域内的任意x都有f(-x)=-f(x),则函数为奇函数.对称轴方程x=k?(k∈Z)对称中心为(k?+ ,0)(k∈Z)余弦函数的对称性由于正、余弦曲线无限延伸,对称轴、对称中心有无限多个.yxo-?-12?3?4?-2?-3?1?余弦曲线:y=cosx,x∈R最值单调性对称性函数性质RRy=sinxy=cosx奇函数:图像关于原点对称偶函数:图像关于y轴对称单调性值 域最 值提升总结:正弦和余弦函数的性质对比y?[ - 1, 1 ]y?[ - 1, 1 ]y=sinxy=cosx例1 画出函数 的简图,根据
图像讨论函数的性质.xy=cosx0 0-1-2-1 0 0-101解:列表1y=cosx-1巩固新知:y=cosx-1 (2)描点
(3)连线(1)列表 R[-2,0]偶函数2π思考交流:≥解:1.用五点法画函数y=2cosx,x?R的图像.y=2cosx y=cosx 解:1.用五点法画函数y=2cosx,x?R的图像.y=2cosx ,x?R由周期性得整个图像.yxo-?-22?2?y=2cosx y=cosx 2.判断函数的奇偶性:..1、余弦函数图像(余弦曲线)y=cosx,x?R2.三角函数的基本性质定义域、值域、周期性、奇偶性、单调性、对称性代数描点法(五点作图)图像平移变换法说一说,你收获了什么?余弦曲线:y=cosx,x∈R 3.学习方法:数形结合的方法
类比的学习方法
布置作业
必做:
课堂作业:教材p34:习题1-6;A组的第2题
家庭作业:本节练习资料
选做:教材p34:习题1-6;B组第1、2题
单位:太和二中
§6 余弦函数的图像与性质y1.会用“图像变换法”和“五点法”作余弦函数的图像.(重点)
2.掌握余弦函数y=cosx的图像和性质.(重点)
3.会应用余弦函数y=cosx的图像与性质解决一些简单问题.(难点)y=sinx x?[0,2?]y=sinx x?Rsin(x+2k?)=sinx, k?Z 正弦函数的图像函数y=sinx, x?R的图象正弦曲线复习回顾 余弦函数y=cosx (x∈R) 的图像 思考:如何将余弦函数用诱导公式写成正弦函数? 方法一(平移法):
余弦曲线的图像可以通过将正弦曲线向左平移 个单位长度而得到.余弦函数的图像叫作余弦曲线.根据诱导公式,可得:课堂探究探究1余弦函数的图象 正弦函数的图象 余弦曲线正弦曲线形状完全一样只是位置不同由未知向已知转化方法:利用图像平移合作探究最高点:最低点:与x轴的交点:-1方法二(五点法):由部分到整体余弦曲线 y=cosx (x?R) 定义域值 域周期性x?Ry?[ - 1, 1 ]T = 2? 余弦函数的性质余弦曲线:y=cosx,x∈R探究2 余弦函数的单调性 y=cosx (x?R)的单调区间: 1 -1 -1cos(-x)= cosx (x?R) 余弦函数的奇偶性关于y轴对称x思考2:如何判断三角函数的奇偶性?
提示:(1)利用图像法:若图像关于原点对称,则函数为奇函数;若图像关于y轴对称,则函数为偶函数.
(2)根据奇偶性的定义判断:若对定义域内的任意x都有f(-x)=f(x),则函数为偶函数;若对定义域内的任意x都有f(-x)=-f(x),则函数为奇函数.对称轴方程x=k?(k∈Z)对称中心为(k?+ ,0)(k∈Z)余弦函数的对称性由于正、余弦曲线无限延伸,对称轴、对称中心有无限多个.yxo-?-12?3?4?-2?-3?1?余弦曲线:y=cosx,x∈R最值单调性对称性函数性质RRy=sinxy=cosx奇函数:图像关于原点对称偶函数:图像关于y轴对称单调性值 域最 值提升总结:正弦和余弦函数的性质对比y?[ - 1, 1 ]y?[ - 1, 1 ]y=sinxy=cosx例1 画出函数 的简图,根据
图像讨论函数的性质.xy=cosx0 0-1-2-1 0 0-101解:列表1y=cosx-1巩固新知:y=cosx-1 (2)描点
(3)连线(1)列表 R[-2,0]偶函数2π思考交流:≥解:1.用五点法画函数y=2cosx,x?R的图像.y=2cosx y=cosx 解:1.用五点法画函数y=2cosx,x?R的图像.y=2cosx ,x?R由周期性得整个图像.yxo-?-22?2?y=2cosx y=cosx 2.判断函数的奇偶性:..1、余弦函数图像(余弦曲线)y=cosx,x?R2.三角函数的基本性质定义域、值域、周期性、奇偶性、单调性、对称性代数描点法(五点作图)图像平移变换法说一说,你收获了什么?余弦曲线:y=cosx,x∈R 3.学习方法:数形结合的方法
类比的学习方法
布置作业
必做:
课堂作业:教材p34:习题1-6;A组的第2题
家庭作业:本节练习资料
选做:教材p34:习题1-6;B组第1、2题
