7.2正切函数的图像与性质 课件(27张PPT)
文档属性
| 名称 | 7.2正切函数的图像与性质 课件(27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-20 22:48:23 | ||
图片预览





文档简介
课件27张PPT。正切函数的图像和性质教学目标 会用单位圆内的正切线画正切曲线,并根据正切函数图象掌握正切函数的性质,用数形结合的思想理解和处理问题。
教学重点难点教学重点:正切函数的图象及其主要性质。
教学难点:利用正切线画出函数y=tanx的图象,对直线x= , 是y=tanx的渐近线的理解,对单调性这个性质的理解。作函数图象常用的方法 一、描点法是作函数图象最基本的方法
二、利用基本初等函数图象的变换作图
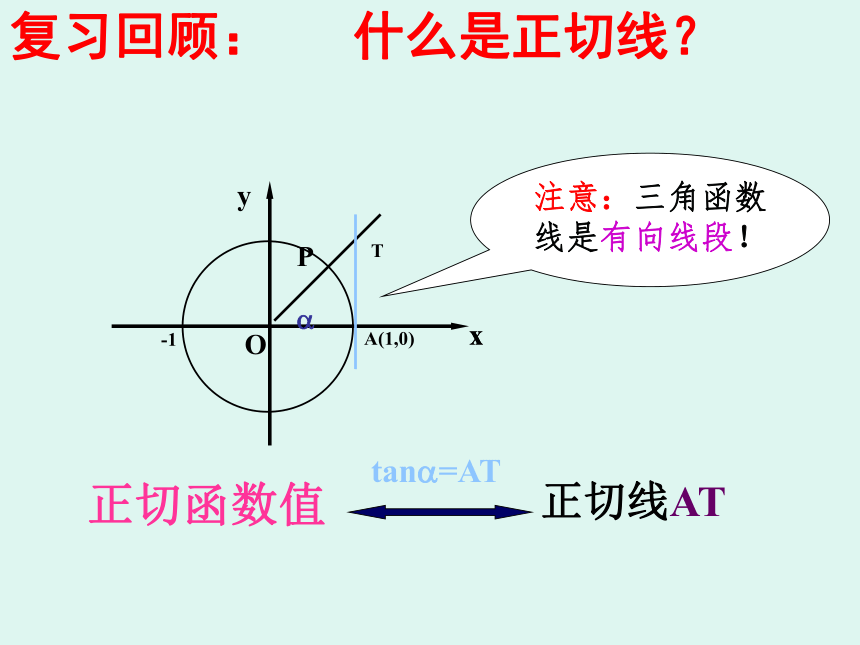
思考正切函数值?PA(1,0)Ttan?=AT正切线AT注意:三角函数线是有向线段!
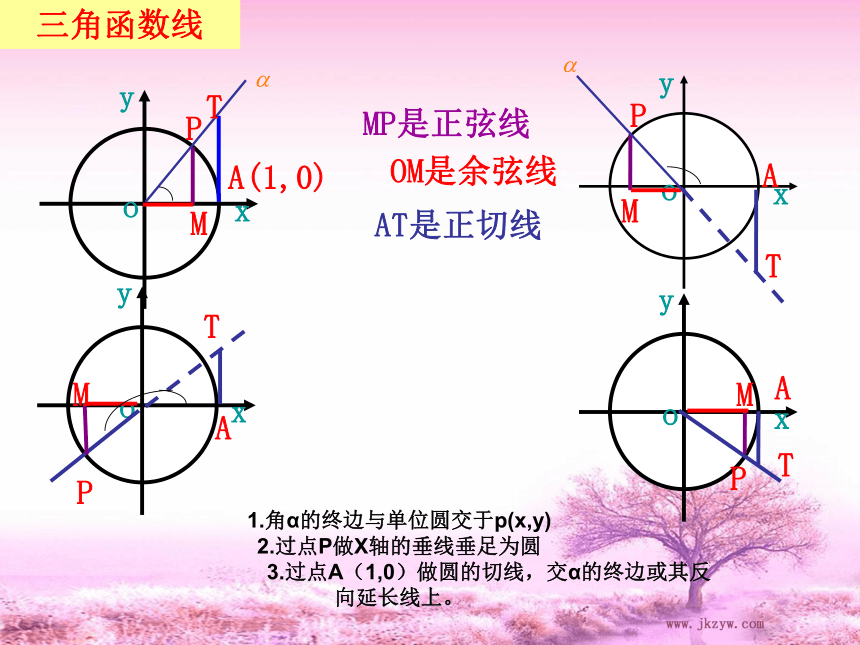
复习回顾: 什么是正切线?三角函数线MPA(1,0)TMP是正弦线OM是余弦线 AT是正切线MPATMPATPMAT1.角α的终边与单位圆交于p(x,y)
2.过点P做X轴的垂线垂足为圆
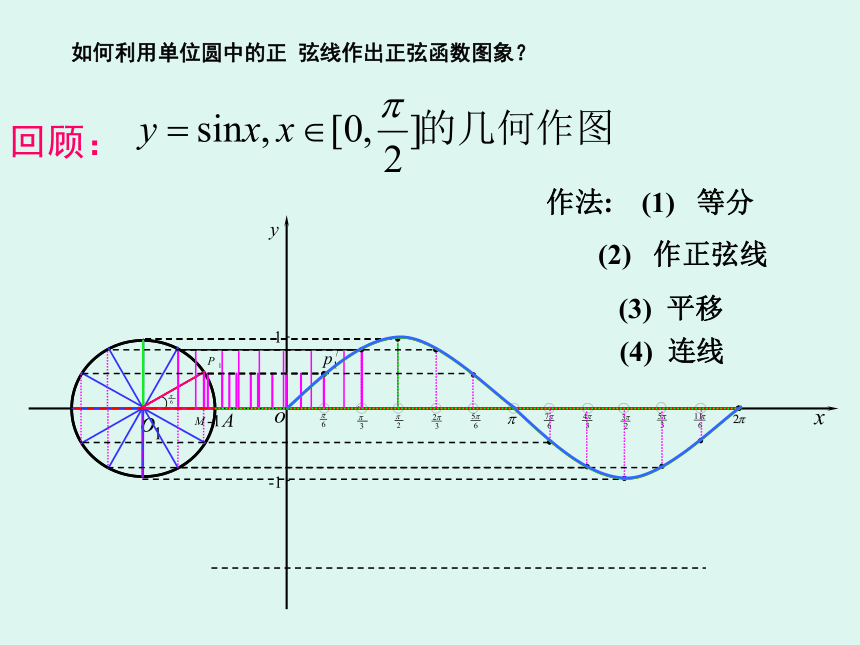
3.过点A(1,0)做圆的切线,交α的终边或其反向延长线上。周期函数:一般地,对于函数f(x),如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有 f(x+T)=f(x),那么这个函数f(x)就叫周期函数。最小正周期:所有周期T中最小的正数。什么是周期函数?作法:(1) 等分(2) 作正弦线(3) 平移(4) 连线回顾:如何利用单位圆中的正 弦线作出正弦函数图象?思考:
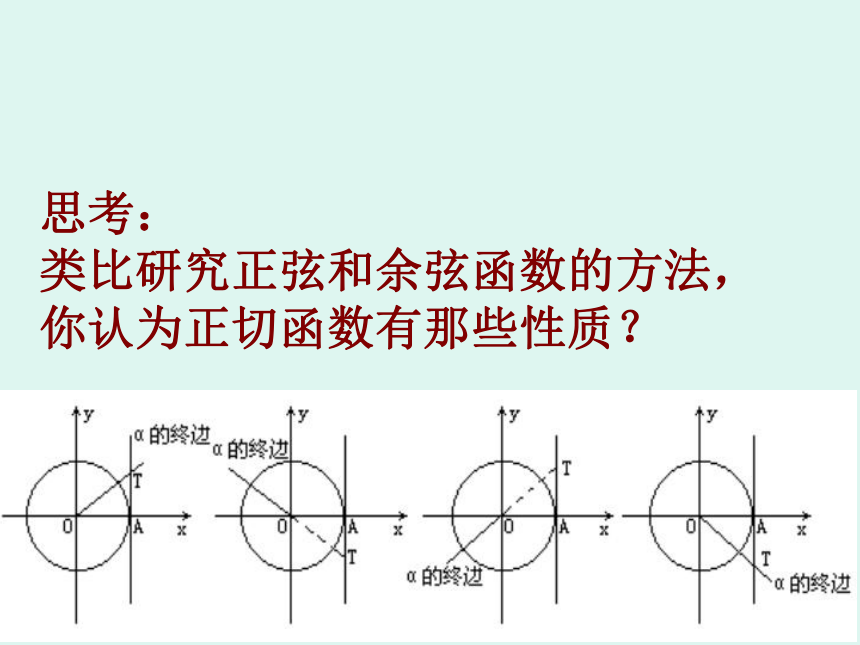
类比研究正弦和余弦函数的方法,
你认为正切函数有那些性质?1.4.3 正切函数的性质与图像
1、利用正切函数的定义,说出正切函数的定义域;温故知新温故知新1、利用正切函数的定义,说出正切函数的定义域。根据诱导公式填空:所以,正切函数是周期函数,且周期是______.tanxπ 首先我们一起分析一下正切函数y=tanx 是否为周期函数?根据诱导公式填空:所以,正切函数是_______函数.奇-tanx接着我们一起分析一下正切函数y=tanx 的奇偶性。 类似正弦曲线的作法,我们先作正切函数在一个周期上的图象。下面我们利用正切线画出函数 请同学们根据所学知识设计一个研究正切函 数图象与性质的方案 方案:第一步:画出正切函数在一个周期内的图象;
第二步:将图象向左、向右平移拓展到整个定义域上去;探究性学习一作法:(1) 等分:(2) 作正切线(3) 平移(4) 连线把单位圆右半圆分成8等份。yx1-1?/2-?/2?3?/2-3?/2-?0定义域值域周期性奇偶性单调性 RT= ?奇函数 函数y=tanxtt+?t-?分小组根据正切函数图象去验证正切函数已有的性质,
并找出其它的性质 探究性学习二正切函数是整个定义域上的增函数吗?为什么?问题讨论A 是奇函数
B 在整个定义域上是增函数
C 在定义域内无最大值和最小值
D 平行于 轴的的直线被正切曲线各支所截线段相等
1.关于正切函数 , 下列判断不正确的是( )基础练习B例1 求函数 的定义域。
解:令 则函数 的定义域是由 可得:
所以函数 的定义域是:
例2、比较下列每组数的大小。说明:比较两个正切值大小,关键是把相应的角 化到y=tanx的同一单调区间内,再利用y=tanx的单调递增性解决。解:例3 求下列函数的周期:由上面两例,你能得到函数y=Atan(ωx+Ф)的周期吗?反馈练习:求下列函数的周期:小结理解正切函数的定义
掌握了正切函数的图象
理解了正切函数的基本性质。
运用了举反例、类比等数学方法体会了数形结合的思想
体验了成功的快乐
作业1、所有同学完成课本57页练习A第4,5题。
2、请每位同学结合今天研究的内容,自己设计一道作业并完成。解:例 5练习反馈典型例题解:
教学重点难点教学重点:正切函数的图象及其主要性质。
教学难点:利用正切线画出函数y=tanx的图象,对直线x= , 是y=tanx的渐近线的理解,对单调性这个性质的理解。作函数图象常用的方法 一、描点法是作函数图象最基本的方法
二、利用基本初等函数图象的变换作图
思考正切函数值?PA(1,0)Ttan?=AT正切线AT注意:三角函数线是有向线段!
复习回顾: 什么是正切线?三角函数线MPA(1,0)TMP是正弦线OM是余弦线 AT是正切线MPATMPATPMAT1.角α的终边与单位圆交于p(x,y)
2.过点P做X轴的垂线垂足为圆
3.过点A(1,0)做圆的切线,交α的终边或其反向延长线上。周期函数:一般地,对于函数f(x),如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有 f(x+T)=f(x),那么这个函数f(x)就叫周期函数。最小正周期:所有周期T中最小的正数。什么是周期函数?作法:(1) 等分(2) 作正弦线(3) 平移(4) 连线回顾:如何利用单位圆中的正 弦线作出正弦函数图象?思考:
类比研究正弦和余弦函数的方法,
你认为正切函数有那些性质?1.4.3 正切函数的性质与图像
1、利用正切函数的定义,说出正切函数的定义域;温故知新温故知新1、利用正切函数的定义,说出正切函数的定义域。根据诱导公式填空:所以,正切函数是周期函数,且周期是______.tanxπ 首先我们一起分析一下正切函数y=tanx 是否为周期函数?根据诱导公式填空:所以,正切函数是_______函数.奇-tanx接着我们一起分析一下正切函数y=tanx 的奇偶性。 类似正弦曲线的作法,我们先作正切函数在一个周期上的图象。下面我们利用正切线画出函数 请同学们根据所学知识设计一个研究正切函 数图象与性质的方案 方案:第一步:画出正切函数在一个周期内的图象;
第二步:将图象向左、向右平移拓展到整个定义域上去;探究性学习一作法:(1) 等分:(2) 作正切线(3) 平移(4) 连线把单位圆右半圆分成8等份。yx1-1?/2-?/2?3?/2-3?/2-?0定义域值域周期性奇偶性单调性 RT= ?奇函数 函数y=tanxtt+?t-?分小组根据正切函数图象去验证正切函数已有的性质,
并找出其它的性质 探究性学习二正切函数是整个定义域上的增函数吗?为什么?问题讨论A 是奇函数
B 在整个定义域上是增函数
C 在定义域内无最大值和最小值
D 平行于 轴的的直线被正切曲线各支所截线段相等
1.关于正切函数 , 下列判断不正确的是( )基础练习B例1 求函数 的定义域。
解:令 则函数 的定义域是由 可得:
所以函数 的定义域是:
例2、比较下列每组数的大小。说明:比较两个正切值大小,关键是把相应的角 化到y=tanx的同一单调区间内,再利用y=tanx的单调递增性解决。解:例3 求下列函数的周期:由上面两例,你能得到函数y=Atan(ωx+Ф)的周期吗?反馈练习:求下列函数的周期:小结理解正切函数的定义
掌握了正切函数的图象
理解了正切函数的基本性质。
运用了举反例、类比等数学方法体会了数形结合的思想
体验了成功的快乐
作业1、所有同学完成课本57页练习A第4,5题。
2、请每位同学结合今天研究的内容,自己设计一道作业并完成。解:例 5练习反馈典型例题解:
