必修4 第一章三角函数 1.8 函数y=Asin(ωx+ψ)的图像 课件(19张PPT)
文档属性
| 名称 | 必修4 第一章三角函数 1.8 函数y=Asin(ωx+ψ)的图像 课件(19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 321.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-20 00:00:00 | ||
图片预览






文档简介
课件19张PPT。§8. 体会如何用y=sinx函数研究y=Asin(ωx+φ)的图像与性质【教材分析】
一、地位与作用:
本节课内容是普通高中课程标准实验教科书北师
大《数学(必修四)》第一章第8节主要讲述利
用函数研究函数图像与性质。本节知识上承正弦
、余弦、正切函数图像与性质,下启三角函数图
像与性质实际应用。同时,三角函数是描述周期现
象的数学模型,在数学和其他领域中具有重要的作用。
二、内容分析:
本节教材对内容的安排主线是:现实背景(的感知
与认识)—建构数学(形成函数概念)—具体化研
究(具体三角函数图像)—数学应用(会作简单函
数图象);此外,通过对例题的安排,介绍了得出
函数图像两种方法。即“五点法”与“变换法”,
充分体现了由“感性认识→理性认识”的认知升华。【三维目标】
一、知识与技能:
1、会作一些简单的、常见的函数图像;
2、能写出简单三角函数函数的性质。
二、过程与方法:
1、结合复习,理解对三种基本变换变化规律;
2、通过对函数了解与认识,学会“五点法”作此图像;
3、利用变换法得到函数图像探索与发现,能写出变换
过程;
三、情感价值观:
1、通过对实际背景(现实原型)的分析、概括与抽象、
形成函数模型,让学生体会数学知识的发生、发展再现
过程,激发学生的学习兴趣和求知欲。
2、通过数学运用,让学生在尝试问题解决中,获得成
功的体验,在数学学习中享受生活,享受快乐。 【重点与难点】
一、教学重点
作函数图像方法:“五点法”与“变换法”及初步应用
二、教学难点
对作函数图像方法:“五点法”与“变换法”
理解及应用【学生分析】
1、知识基础:学生认识了正弦、余弦、正切函数图像与性质,有了一定的知识基础;
2、生活基础:日出日落、四季更替……始终伴随着我们的生活,容易激发学生的兴趣与求知欲;
3、基本能力:在建构主义教学理论指导下的数学学习,使学生已经具备了一定的观察、分析、思考的能力,为本节课的展开提供了可能。【教法与学法】
一、学法设计:
学法设计主要有:
观察、思考、小组讨论、合作探究。在理论形成阶
段主要以小组形式参与研究学习;在数学运用阶段
主要以自主学习为主,检验学生理解与掌
握情况。
二、教法设计:
教法设计主要有:启发、引导。【教学工具】
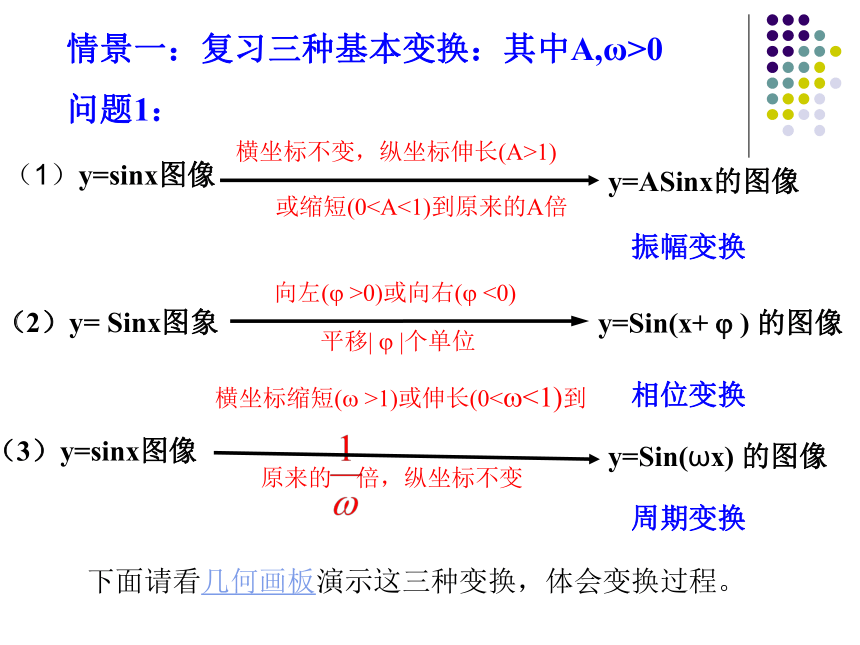
多媒体课件 y=ASinx的图像y=Sin(x+ ? ) 的图像(1)y=sinx图像(2)y= Sinx图象情景一:复习三种基本变换:其中A,ω>0
问题1:下面请看几何画板演示这三种变换,体会变换过程。振幅变换周期变换相位变换y=Sin(ωx) 的图像(3)y=sinx图像电流输出波形图情景二:生活中常见的波形图y=Asin(ωx+ ? )如何作函数y=Asin(ωx+ ?)(A>0,ω>0)图像呢?此类函数有什么性质呢?函数y=Asin(ωx+ ?)与正弦函数y=sinx图像有怎样的关系呢?两者之间有怎样的变化规律.本堂课我们将综合研究A,ω, ?这三个量对函数图像的影响?对于形如y=Asin(ωx+ ?)(其中A, ω>0, ?不为零)
类型的三角函数我们来研究一个具体的函数:问题2:研究函数性质通常采用什么方法?方法引导:常见作图方法:描点法----“五点法”作图解:“五点法”作图步骤:
1.列表:略
2.描出五点:
3.将这五个点用光滑的曲线连接起来,然后根据周期性,将图像向左,右平移得出整个图像.几何画板展示“五点法”作图过程学生活动二:学习小组组合作完成(1)相位-----周期-----振幅归纳上述研究思路问题思考1:
是否只有以上两种变换思路?对于相位、周期与振幅变换它们的顺序可以调换吗?(2)周期-----相位-----振幅(3)振幅-----相位-----周期拓展●引申:
根据以上研究,请分析解决以下问题:
函数y=Asin(ωx+ ? )+b(A>0,ω>0)的图像可由函数y=sinx的图像经过怎样变化得到?方法1:先平移后伸缩方法2:先伸缩后平移理论认识:y=Sinx →y=ASin(?x+ ? )+b 问题思考2:根据以上研究,请分析解决以下问题
参数A,ω,φ对函数y=Asin(ωx+φ)(A>0,ω>0)的图像有什么影响?练习反馈回顾反思小结 5-1、作函数y=Asin(?x+?) 的图像:
(1)用“五点法”作图。
(2)利用变换关系作图。5-2、会用五点法和变换法作三角函数 y=Asin(?x+?)的图像基本技能,利用图像研究三角函数的性质5-3、数形结合思想,分类讨论思想书面作业:
课本56页练习3你学会了吗?再见。谢谢!努力就有收获。思考●运用
函数y=ASin(?x+ ? )+b经过怎样的变化得到函数 y=Sinx
一、地位与作用:
本节课内容是普通高中课程标准实验教科书北师
大《数学(必修四)》第一章第8节主要讲述利
用函数研究函数图像与性质。本节知识上承正弦
、余弦、正切函数图像与性质,下启三角函数图
像与性质实际应用。同时,三角函数是描述周期现
象的数学模型,在数学和其他领域中具有重要的作用。
二、内容分析:
本节教材对内容的安排主线是:现实背景(的感知
与认识)—建构数学(形成函数概念)—具体化研
究(具体三角函数图像)—数学应用(会作简单函
数图象);此外,通过对例题的安排,介绍了得出
函数图像两种方法。即“五点法”与“变换法”,
充分体现了由“感性认识→理性认识”的认知升华。【三维目标】
一、知识与技能:
1、会作一些简单的、常见的函数图像;
2、能写出简单三角函数函数的性质。
二、过程与方法:
1、结合复习,理解对三种基本变换变化规律;
2、通过对函数了解与认识,学会“五点法”作此图像;
3、利用变换法得到函数图像探索与发现,能写出变换
过程;
三、情感价值观:
1、通过对实际背景(现实原型)的分析、概括与抽象、
形成函数模型,让学生体会数学知识的发生、发展再现
过程,激发学生的学习兴趣和求知欲。
2、通过数学运用,让学生在尝试问题解决中,获得成
功的体验,在数学学习中享受生活,享受快乐。 【重点与难点】
一、教学重点
作函数图像方法:“五点法”与“变换法”及初步应用
二、教学难点
对作函数图像方法:“五点法”与“变换法”
理解及应用【学生分析】
1、知识基础:学生认识了正弦、余弦、正切函数图像与性质,有了一定的知识基础;
2、生活基础:日出日落、四季更替……始终伴随着我们的生活,容易激发学生的兴趣与求知欲;
3、基本能力:在建构主义教学理论指导下的数学学习,使学生已经具备了一定的观察、分析、思考的能力,为本节课的展开提供了可能。【教法与学法】
一、学法设计:
学法设计主要有:
观察、思考、小组讨论、合作探究。在理论形成阶
段主要以小组形式参与研究学习;在数学运用阶段
主要以自主学习为主,检验学生理解与掌
握情况。
二、教法设计:
教法设计主要有:启发、引导。【教学工具】
多媒体课件 y=ASinx的图像y=Sin(x+ ? ) 的图像(1)y=sinx图像(2)y= Sinx图象情景一:复习三种基本变换:其中A,ω>0
问题1:下面请看几何画板演示这三种变换,体会变换过程。振幅变换周期变换相位变换y=Sin(ωx) 的图像(3)y=sinx图像电流输出波形图情景二:生活中常见的波形图y=Asin(ωx+ ? )如何作函数y=Asin(ωx+ ?)(A>0,ω>0)图像呢?此类函数有什么性质呢?函数y=Asin(ωx+ ?)与正弦函数y=sinx图像有怎样的关系呢?两者之间有怎样的变化规律.本堂课我们将综合研究A,ω, ?这三个量对函数图像的影响?对于形如y=Asin(ωx+ ?)(其中A, ω>0, ?不为零)
类型的三角函数我们来研究一个具体的函数:问题2:研究函数性质通常采用什么方法?方法引导:常见作图方法:描点法----“五点法”作图解:“五点法”作图步骤:
1.列表:略
2.描出五点:
3.将这五个点用光滑的曲线连接起来,然后根据周期性,将图像向左,右平移得出整个图像.几何画板展示“五点法”作图过程学生活动二:学习小组组合作完成(1)相位-----周期-----振幅归纳上述研究思路问题思考1:
是否只有以上两种变换思路?对于相位、周期与振幅变换它们的顺序可以调换吗?(2)周期-----相位-----振幅(3)振幅-----相位-----周期拓展●引申:
根据以上研究,请分析解决以下问题:
函数y=Asin(ωx+ ? )+b(A>0,ω>0)的图像可由函数y=sinx的图像经过怎样变化得到?方法1:先平移后伸缩方法2:先伸缩后平移理论认识:y=Sinx →y=ASin(?x+ ? )+b 问题思考2:根据以上研究,请分析解决以下问题
参数A,ω,φ对函数y=Asin(ωx+φ)(A>0,ω>0)的图像有什么影响?练习反馈回顾反思小结 5-1、作函数y=Asin(?x+?) 的图像:
(1)用“五点法”作图。
(2)利用变换关系作图。5-2、会用五点法和变换法作三角函数 y=Asin(?x+?)的图像基本技能,利用图像研究三角函数的性质5-3、数形结合思想,分类讨论思想书面作业:
课本56页练习3你学会了吗?再见。谢谢!努力就有收获。思考●运用
函数y=ASin(?x+ ? )+b经过怎样的变化得到函数 y=Sinx
