必修4 第一章三角函数 函数y=Asin(ωx+ψ)的图像 课件(21张PPT)
文档属性
| 名称 | 必修4 第一章三角函数 函数y=Asin(ωx+ψ)的图像 课件(21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 830.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-20 22:50:13 | ||
图片预览





文档简介
课件21张PPT。 在实际问题中,经常会遇到形如y=Asin(ωx+ )的函数(其中A,ω, 是常数),那么这个函数有什么性质?它与y=sinx有什么关系?回顾: y=sinx的图像性质问题引入:2019年12月30日15时34分第一章 三角函数
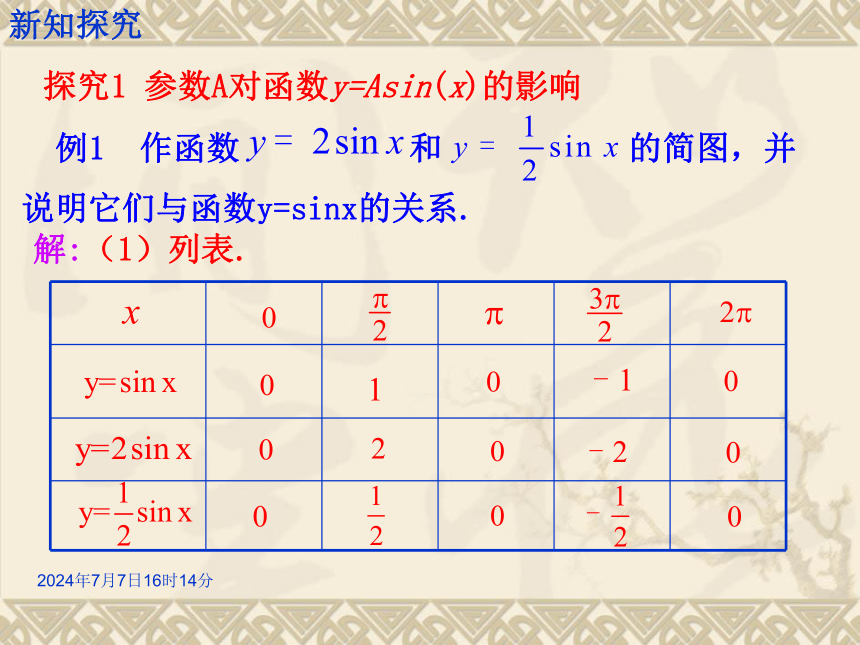
§8函数y=Asin(ωx+φ)的图象与性质2019年12月30日15时34分2019年12月30日15时34分解:(1)列表. 例1 作函数 和 的简图,并
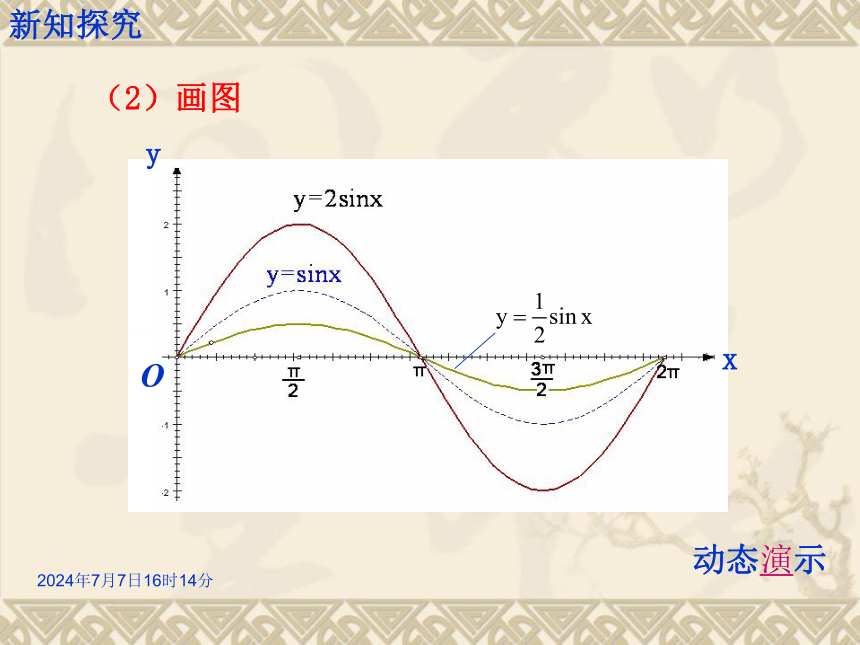
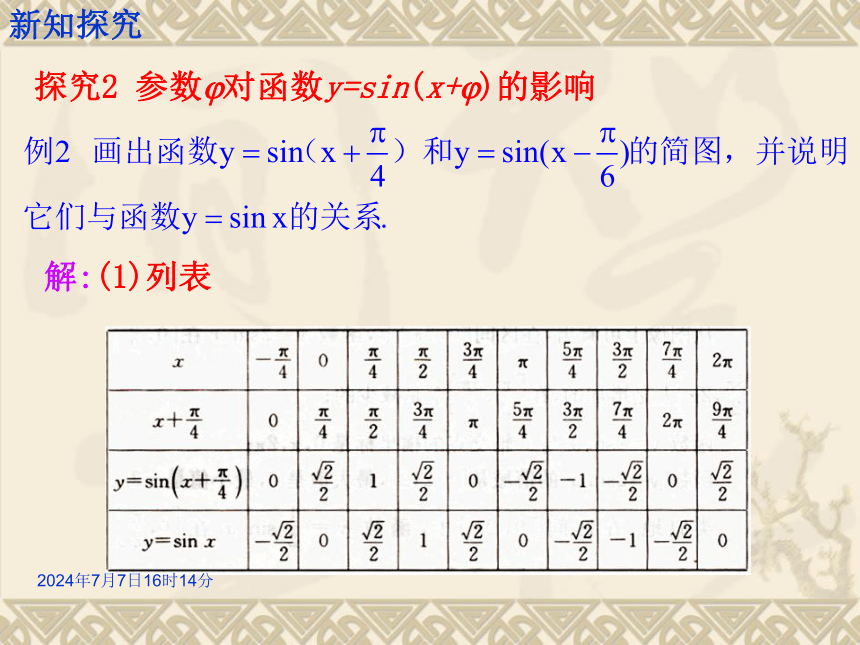
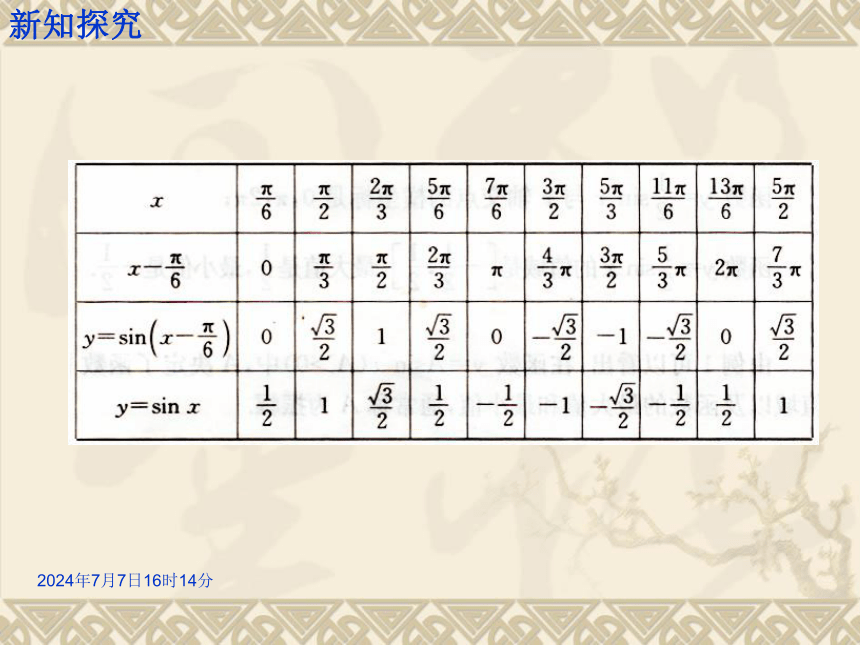
说明它们与函数y=sinx的关系. x探究1 参数A对函数y=Asin(x)的影响新知探究2019年12月30日15时34分(2)画图yOx新知探究动态演示2019年12月30日15时34分 由上例可以看出:在函数y=Asinx(A>0)中,A决定了函数的值域以及函数的最大值和最小值,通常称A为振幅. 函数y=Asinx (A>0且A≠1)的图像可以看作是把y=sinx的图像上所有点的纵坐标变化为原来的A倍(横坐标不变) 而得到的.提升总结:参数A对函数y=Asin(x)的影响新知探究2019年12月30日15时34分描述下列曲线,可以由正弦曲线如何变换得到变式练习:知识应用2019年12月30日15时34分解:(1)列表探究2 参数?对函数y=sin(x+?)的影响新知探究2019年12月30日15时34分新知探究2019年12月30日15时34分(2)画图新知探究动态演示2019年12月30日15时34分函数y=sin(x+?)的图像可以看作是把y=sinx的图像上所有的点向左(当?>0时)或向右(当?<0时)平移|?|个单位长度而得到的. 在函数y=sin(x+φ)中,φ决定了x=0时的函数值,通常称φ为初相,x+φ为相位.提升总结:参数 ?对函数y=sin(x+?)的影响新知探究2019年12月30日15时34分描述下列曲线可以由正弦曲线如何变换得到变式练习:知识应用2019年12月30日15时34分A知识应用2019年12月30日15时34分①列表:例3 画出函数 及 的简图,并
说明它们与函数y=sinx的图像的关系. 采用类比法探究3 参数?对函数y=sin(?x)的影响新知探究2019年12月30日15时34分x?②描点作图:y=sin2x y=sin x新知探究2019年12月30日15时34分①列表:新知探究2019年12月30日15时34分②描点作图:y=sin x新知探究动态演示2019年12月30日15时34分函数y=sin?x (? >0且?≠1)的图像可以看作是把y=sinx的图像上所有点的横坐标变化为原来的 倍(纵坐标不变)而得到的.提升总结:参数 ? 对函数y=sin(?x)的影响新知探究2019年12月30日15时34分描述下列曲线可以由正弦曲线如何变换得到变式练习:知识应用2019年12月30日15时34分 参数A(A>0),ω(ω>0),φ对函数y=Asin(ωx+φ)图像的影响
(1)将函数y=sin(x)的图像上所有点向左(φ>0)或向右(φ<0) 平移|φ|个单位长度得到y=sin(x+φ)的图像.
(2)将函数y=sin(x)的图像上所有点的横坐标缩短(当ω>1时)或伸长(当0<ω<1时)到原来的 倍(纵坐标不变)得到函数y=sin(ωx)的图像.
(3)将函数y=sin(x)的图像上所有点的纵坐标伸长 (当A>1时)或缩短(当0归纳小结2019年12月30日15时34分作业:
习题1---8(A组)
第2、3题2019年12月30日15时34分
§8函数y=Asin(ωx+φ)的图象与性质2019年12月30日15时34分2019年12月30日15时34分解:(1)列表. 例1 作函数 和 的简图,并
说明它们与函数y=sinx的关系. x探究1 参数A对函数y=Asin(x)的影响新知探究2019年12月30日15时34分(2)画图yOx新知探究动态演示2019年12月30日15时34分 由上例可以看出:在函数y=Asinx(A>0)中,A决定了函数的值域以及函数的最大值和最小值,通常称A为振幅. 函数y=Asinx (A>0且A≠1)的图像可以看作是把y=sinx的图像上所有点的纵坐标变化为原来的A倍(横坐标不变) 而得到的.提升总结:参数A对函数y=Asin(x)的影响新知探究2019年12月30日15时34分描述下列曲线,可以由正弦曲线如何变换得到变式练习:知识应用2019年12月30日15时34分解:(1)列表探究2 参数?对函数y=sin(x+?)的影响新知探究2019年12月30日15时34分新知探究2019年12月30日15时34分(2)画图新知探究动态演示2019年12月30日15时34分函数y=sin(x+?)的图像可以看作是把y=sinx的图像上所有的点向左(当?>0时)或向右(当?<0时)平移|?|个单位长度而得到的. 在函数y=sin(x+φ)中,φ决定了x=0时的函数值,通常称φ为初相,x+φ为相位.提升总结:参数 ?对函数y=sin(x+?)的影响新知探究2019年12月30日15时34分描述下列曲线可以由正弦曲线如何变换得到变式练习:知识应用2019年12月30日15时34分A知识应用2019年12月30日15时34分①列表:例3 画出函数 及 的简图,并
说明它们与函数y=sinx的图像的关系. 采用类比法探究3 参数?对函数y=sin(?x)的影响新知探究2019年12月30日15时34分x?②描点作图:y=sin2x y=sin x新知探究2019年12月30日15时34分①列表:新知探究2019年12月30日15时34分②描点作图:y=sin x新知探究动态演示2019年12月30日15时34分函数y=sin?x (? >0且?≠1)的图像可以看作是把y=sinx的图像上所有点的横坐标变化为原来的 倍(纵坐标不变)而得到的.提升总结:参数 ? 对函数y=sin(?x)的影响新知探究2019年12月30日15时34分描述下列曲线可以由正弦曲线如何变换得到变式练习:知识应用2019年12月30日15时34分 参数A(A>0),ω(ω>0),φ对函数y=Asin(ωx+φ)图像的影响
(1)将函数y=sin(x)的图像上所有点向左(φ>0)或向右(φ<0) 平移|φ|个单位长度得到y=sin(x+φ)的图像.
(2)将函数y=sin(x)的图像上所有点的横坐标缩短(当ω>1时)或伸长(当0<ω<1时)到原来的 倍(纵坐标不变)得到函数y=sin(ωx)的图像.
(3)将函数y=sin(x)的图像上所有点的纵坐标伸长 (当A>1时)或缩短(当0
习题1---8(A组)
第2、3题2019年12月30日15时34分
