必修4 第一章三角函数 同角三角函数的基本关系(一) 课件(18张PPT)
文档属性
| 名称 | 必修4 第一章三角函数 同角三角函数的基本关系(一) 课件(18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-20 00:00:00 | ||
图片预览






文档简介
课件18张PPT。第三章 三角恒等变形
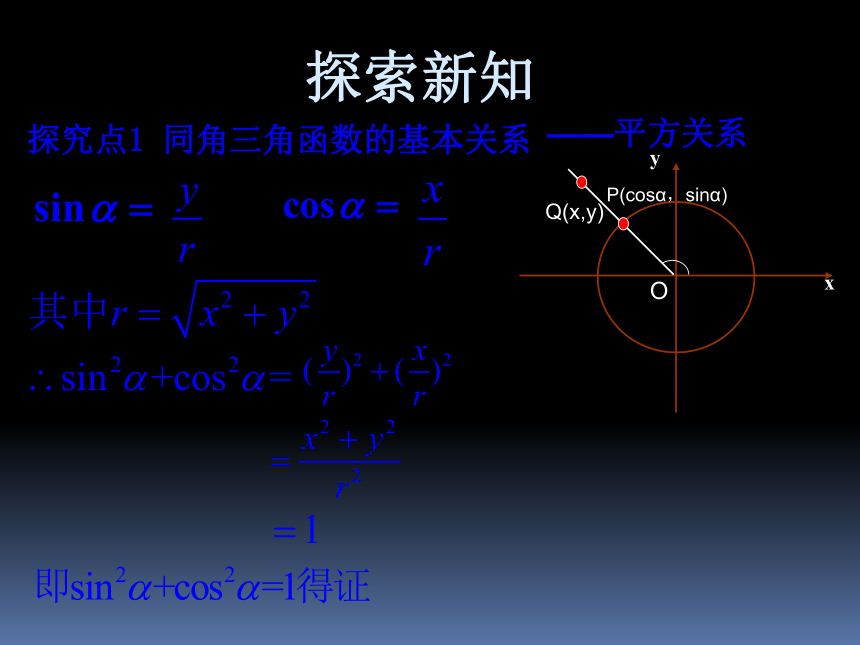
§1 同角三角函数的基本关系(1) 在初中我们已经知道,对于同一个锐角 α ,存在关系式:当角α推广到任意角后,关系式是否仍成立?复习引入提示:利用三角函数定义证明探究点1 同角三角函数的基本关系探索新知——平方关系P(cosα,sinα)Q(x,y)判一判 (正确的打“√”,错误的打“×”)
(1)对任意角α,sin α2+cos α2=1都成立.( )
(2)对任意角α, 都成立.( )
(3)对任意角α、β,sin2α+cos2β=1都成立.( )特别注意:2、对“同角” 的含义理解“同角”即“角相同”如 与 ,2α与2α都是同角 1、√×× 探究点2 同角三角函数的基本关系——商数关系判一判 (正确的打“√”,错误的打“×”)
对任意角α, 都成立.( )×商数关系 不是对任意角都成立,是在等式两边都有意义的情况 下,等式才成立.特别注意:P(cosα,sinα)Q(x,y)公式可以变形使用: 哇!还有变形! 平方关系:商数关系:例1提示:利用三角函数定义求解解:-4-3(-4,-3)例1解法二:∵α在第三象限,则cosα< 0 例1解:∵α在第三象限,则cosα< 0 ,变式:①②-4-3(-4,-3)4(4,-3)变式:注意:2.已知函数值,由值定象限,进而确定符号1.已知象限,由象限确定符号;解:小试牛刀:解:例2 已知 , ,求 的值分子分母同时除以cosα分子分母同时除以cosα分析:小试牛刀:解:(1)原式=(2)原式=本节课主要学习了:1.用三角函数定义证明同角三角函数的基本关系2.利用同角三角函数的基本关系求值以及公式的灵活应用平方关系:商数关系:sinα、cosα、tanα,“知一求二”注意:1.已知象限,由象限确定符号;2.已知函数值,由值定象限3.值是字母,分类讨论课后练习:课本习题 A组题第1题(2)(3)
第2题光阴给我们经验,读书给我们知识.
——奥斯特洛夫斯基
§1 同角三角函数的基本关系(1) 在初中我们已经知道,对于同一个锐角 α ,存在关系式:当角α推广到任意角后,关系式是否仍成立?复习引入提示:利用三角函数定义证明探究点1 同角三角函数的基本关系探索新知——平方关系P(cosα,sinα)Q(x,y)判一判 (正确的打“√”,错误的打“×”)
(1)对任意角α,sin α2+cos α2=1都成立.( )
(2)对任意角α, 都成立.( )
(3)对任意角α、β,sin2α+cos2β=1都成立.( )特别注意:2、对“同角” 的含义理解“同角”即“角相同”如 与 ,2α与2α都是同角 1、√×× 探究点2 同角三角函数的基本关系——商数关系判一判 (正确的打“√”,错误的打“×”)
对任意角α, 都成立.( )×商数关系 不是对任意角都成立,是在等式两边都有意义的情况 下,等式才成立.特别注意:P(cosα,sinα)Q(x,y)公式可以变形使用: 哇!还有变形! 平方关系:商数关系:例1提示:利用三角函数定义求解解:-4-3(-4,-3)例1解法二:∵α在第三象限,则cosα< 0 例1解:∵α在第三象限,则cosα< 0 ,变式:①②-4-3(-4,-3)4(4,-3)变式:注意:2.已知函数值,由值定象限,进而确定符号1.已知象限,由象限确定符号;解:小试牛刀:解:例2 已知 , ,求 的值分子分母同时除以cosα分子分母同时除以cosα分析:小试牛刀:解:(1)原式=(2)原式=本节课主要学习了:1.用三角函数定义证明同角三角函数的基本关系2.利用同角三角函数的基本关系求值以及公式的灵活应用平方关系:商数关系:sinα、cosα、tanα,“知一求二”注意:1.已知象限,由象限确定符号;2.已知函数值,由值定象限3.值是字母,分类讨论课后练习:课本习题 A组题第1题(2)(3)
第2题光阴给我们经验,读书给我们知识.
——奥斯特洛夫斯基
