人教版选修1-1 1.2.1充分条件与必要条件课件(32张)
文档属性
| 名称 | 人教版选修1-1 1.2.1充分条件与必要条件课件(32张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-20 00:00:00 | ||
图片预览










文档简介
课件32张PPT。1.2.1 充分条件与必要条件
1.结合具体实例,理解充分条件、必要条件的意义.
2.掌握充分条件、必要条件的判断方法.
3.通过对充分条件、必要条件的概念的理解和运用,培养分析、判断和归纳的逻辑思维能力.学习目标题型探究问题导学内容索引当堂训练问题导学思考1 你能判断这两个命题的真假吗? 知识点一 充分条件与必要条件的概念给出下列命题:
(1)若x>a2+b2,则x>2ab;
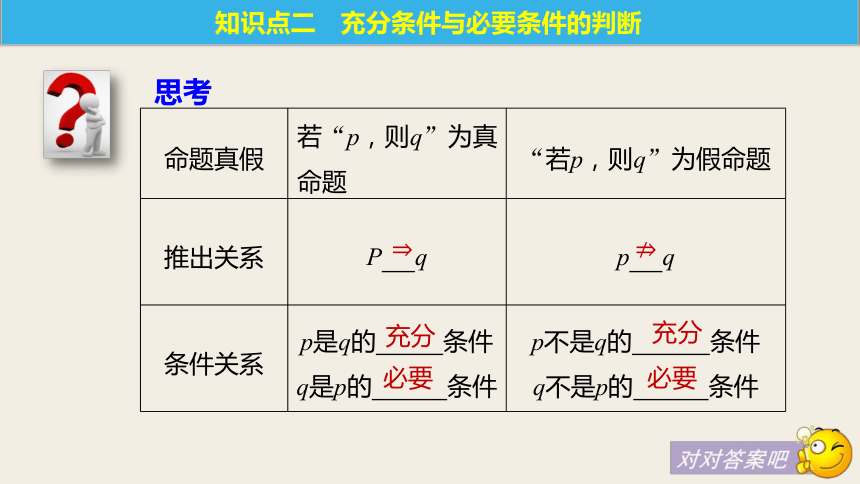
(2)若ab=0,则a=0.答案(1)真命题;(2)假命题.思考2 命题(1)中条件和结论有什么关系?命题(2)中呢?答案命题(1)中只要满足条件x>a2+b2,必有结论x>2ab;命题(2)中满足条件ab=0,不一定有结论a=0,还可能有结论b=0.梳理 一般地,“若p,则q”为真命题,是指由p通过推理可以得出q.这时,我们就说,由p可推出q,记作 ,并且说p是q的
,q是p的 .p?q充分条件必要条件知识点二 充分条件与必要条件的判断思考 ??充分必要充分必要知识点三 充分条件、必要条件与集合的关系思考“x<2”是“x<3”的_____条件,“x<3”是“x<2”的____条件.答案充分必要梳理 A={x|x满足条件p},B={x|x满足条件q}题型探究例1 (1)判断下列说法中,p是q的充分条件的是____.
①p:“x=1”,q:“x2-2x+1=0”;
②已知α,β是不同的两个平面,直线a?α,直线b?β,p:a与b无公共点,q:α∥β;
③设a,b是实数,p:“a+b>0”,q:“ab>0”.类型一 充分条件与必要条件的概念对①,p?q;②p?q;③p?q,故选①.①(2)下列各题中,p是q的必要条件的是________.
①p:x2>2 016,q:x2>2 015;
②p:ax2+2ax+1>0的解集是实数集R,q:0③已知a,b为正实数,p:a>b>1,q:log2a>log2b>0.①q?p;②p:0≤a<1,故q?p;
③log2a>log2b>0?a>b>1,
∴q?p,故选②③.②③引申探究
例1 (1)中p是q的必要条件是________.
①②①x2-2x+1=0?x=1,即q?p;③q?p.故选①②.充分条件、必要条件的两种判断方法
(1)定义法
①确定谁是条件,谁是结论;
②尝试从条件推结论,若条件能推出结论,则条件为结论的充分条件,否则就不是充分条件;
③尝试从结论推条件,若结论能推出条件,则条件为结论的必要条件,否则就不是必要条件.(2)命题判断法
①如果命题:“若p,则q”为真命题,那么p是q的充分条件,同时q是p的必要条件;
②如果命题:“若p,则q”为假命题,那么p不是q的充分条件,同时q也不是p的必要条件. 跟踪训练1 对任意实数a,b,c,在下列命题中,真命题是
A.“ac>bc”是“a>b”的必要条件
B.“ac=bc”是“a=b”的必要条件
C.“ac>bc”是“a>b”的充分条件
D.“ac=bc”是“a=b”的充分条件
∴ac>bc?a>b,而由a>b?ac>bc,
∴“ac>bc”既不是“a>b”的充分条件,也不是必要条件,
故A,C错误.
∴由ac=bc?a=b,
而由a=b?ac=bc,
∴“ac=bc”是“a=b”的必要不充分条件,故选B.类型二 充分条件与必要条件的应用例2 已知p:x2-x-6≤0,q:x2-4x+4-9m2≤0,若q是p的充分条件,求正实数m的取值范围.解不等式得p:-2≤x≤3,
当m>0时,q:2-3m≤x≤2+3m,
由q是p的充分条件可得q?p,
所以正实数m的取值范围为0本例条件变为q是p的必要条件,求正实数m的取值范围.由p:-2≤x≤3,q:2-3m≤x≤2+3m(m>0),
∵q是p的必要条件,∴p?q,
(1)设集合A={x|x满足p},B={x|x满足q},则p?q可得A?B;q?p可得B?A;p?q可得A=B,若p是q的充分不必要条件,则A?B.
(2)利用充分条件、必要条件求参数的取值范围的关键就是找出集合间的包含关系,要注意范围的临界值.跟踪训练2 已知p:x<-2或x>10,q:x2-2x+1-a2>0,若p是q的必要条件,求负实数a的取值范围.∵a<0,解不等式得q:x<1+a或x>1-a,
∵p是q的必要条件,∴q?p,
故负实数a的取值范围是a≤-9.当堂训练∵x>2?x>1,
∴x>1是x>2的必要条件.1.设x∈R,则x>2的一个必要条件是
A.x>1 B.x<1
C.x>3 D.x<31234√512342.若a∈R,则“a=2”是“(a-1)(a-2)=0”的
A.充分条件
B.必要条件
C.既不是充分条件,也不是必要条件
D.无法判断√5∵a=2?(a-1)(a-2)=0,
∴a=2是(a-1)(a-2)=0的充分条件.123453.设向量a=(2,x-1),b=(x+1,4),则“x=3”是“a∥b”的
A.充分条件
B.必要条件
C.既不是充分条件,又不是必要条件
D.无法判断√∵a∥b,∴(x-1)(x+1)-8=0,
解得x=±3,
∴x=3是a∥b的充分条件.123454.已知p:-4123455.是否存在实数p,使得x2-x-2>0的一个充分条件是4x+p<0,若存在,求出p的取值范围,否则,说明理由.12345
由x2-x-2>0,解得x>2或x<-1.
令A={x|x>2或x<-1},∴当p≥4时,“4x+p<0”是“x2-x-2>0”的一个充分条件.1.充分条件、必要条件的判断方法
(1)定义法:直接利用定义进行判断.
(2)等价法:“p?q”表示p等价于q,等价命题可以进行转换,当我们要证明p成立时,就可以去证明q成立.
(3)利用集合间的包含关系进行判断:如果条件p和结论q相应的集合分别为A和B,那么若A?B,则p是q的充分条件;若A?B,则p是q的必要条件;若A=B,则p是q的充分必要条件.
2.根据充分条件、必要条件求参数的取值范围时,主要根据充分条件、必要条件与集合间的关系,将问题转化为相应的两个集合之间的包含关系,然后建立关于参数的不等式(组)进行求解.本课结束
1.结合具体实例,理解充分条件、必要条件的意义.
2.掌握充分条件、必要条件的判断方法.
3.通过对充分条件、必要条件的概念的理解和运用,培养分析、判断和归纳的逻辑思维能力.学习目标题型探究问题导学内容索引当堂训练问题导学思考1 你能判断这两个命题的真假吗? 知识点一 充分条件与必要条件的概念给出下列命题:
(1)若x>a2+b2,则x>2ab;
(2)若ab=0,则a=0.答案(1)真命题;(2)假命题.思考2 命题(1)中条件和结论有什么关系?命题(2)中呢?答案命题(1)中只要满足条件x>a2+b2,必有结论x>2ab;命题(2)中满足条件ab=0,不一定有结论a=0,还可能有结论b=0.梳理 一般地,“若p,则q”为真命题,是指由p通过推理可以得出q.这时,我们就说,由p可推出q,记作 ,并且说p是q的
,q是p的 .p?q充分条件必要条件知识点二 充分条件与必要条件的判断思考 ??充分必要充分必要知识点三 充分条件、必要条件与集合的关系思考“x<2”是“x<3”的_____条件,“x<3”是“x<2”的____条件.答案充分必要梳理 A={x|x满足条件p},B={x|x满足条件q}题型探究例1 (1)判断下列说法中,p是q的充分条件的是____.
①p:“x=1”,q:“x2-2x+1=0”;
②已知α,β是不同的两个平面,直线a?α,直线b?β,p:a与b无公共点,q:α∥β;
③设a,b是实数,p:“a+b>0”,q:“ab>0”.类型一 充分条件与必要条件的概念对①,p?q;②p?q;③p?q,故选①.①(2)下列各题中,p是q的必要条件的是________.
①p:x2>2 016,q:x2>2 015;
②p:ax2+2ax+1>0的解集是实数集R,q:0
③log2a>log2b>0?a>b>1,
∴q?p,故选②③.②③引申探究
例1 (1)中p是q的必要条件是________.
①②①x2-2x+1=0?x=1,即q?p;③q?p.故选①②.充分条件、必要条件的两种判断方法
(1)定义法
①确定谁是条件,谁是结论;
②尝试从条件推结论,若条件能推出结论,则条件为结论的充分条件,否则就不是充分条件;
③尝试从结论推条件,若结论能推出条件,则条件为结论的必要条件,否则就不是必要条件.(2)命题判断法
①如果命题:“若p,则q”为真命题,那么p是q的充分条件,同时q是p的必要条件;
②如果命题:“若p,则q”为假命题,那么p不是q的充分条件,同时q也不是p的必要条件. 跟踪训练1 对任意实数a,b,c,在下列命题中,真命题是
A.“ac>bc”是“a>b”的必要条件
B.“ac=bc”是“a=b”的必要条件
C.“ac>bc”是“a>b”的充分条件
D.“ac=bc”是“a=b”的充分条件
∴ac>bc?a>b,而由a>b?ac>bc,
∴“ac>bc”既不是“a>b”的充分条件,也不是必要条件,
故A,C错误.
∴由ac=bc?a=b,
而由a=b?ac=bc,
∴“ac=bc”是“a=b”的必要不充分条件,故选B.类型二 充分条件与必要条件的应用例2 已知p:x2-x-6≤0,q:x2-4x+4-9m2≤0,若q是p的充分条件,求正实数m的取值范围.解不等式得p:-2≤x≤3,
当m>0时,q:2-3m≤x≤2+3m,
由q是p的充分条件可得q?p,
所以正实数m的取值范围为0
∵q是p的必要条件,∴p?q,
(1)设集合A={x|x满足p},B={x|x满足q},则p?q可得A?B;q?p可得B?A;p?q可得A=B,若p是q的充分不必要条件,则A?B.
(2)利用充分条件、必要条件求参数的取值范围的关键就是找出集合间的包含关系,要注意范围的临界值.跟踪训练2 已知p:x<-2或x>10,q:x2-2x+1-a2>0,若p是q的必要条件,求负实数a的取值范围.∵a<0,解不等式得q:x<1+a或x>1-a,
∵p是q的必要条件,∴q?p,
故负实数a的取值范围是a≤-9.当堂训练∵x>2?x>1,
∴x>1是x>2的必要条件.1.设x∈R,则x>2的一个必要条件是
A.x>1 B.x<1
C.x>3 D.x<31234√512342.若a∈R,则“a=2”是“(a-1)(a-2)=0”的
A.充分条件
B.必要条件
C.既不是充分条件,也不是必要条件
D.无法判断√5∵a=2?(a-1)(a-2)=0,
∴a=2是(a-1)(a-2)=0的充分条件.123453.设向量a=(2,x-1),b=(x+1,4),则“x=3”是“a∥b”的
A.充分条件
B.必要条件
C.既不是充分条件,又不是必要条件
D.无法判断√∵a∥b,∴(x-1)(x+1)-8=0,
解得x=±3,
∴x=3是a∥b的充分条件.123454.已知p:-4
由x2-x-2>0,解得x>2或x<-1.
令A={x|x>2或x<-1},∴当p≥4时,“4x+p<0”是“x2-x-2>0”的一个充分条件.1.充分条件、必要条件的判断方法
(1)定义法:直接利用定义进行判断.
(2)等价法:“p?q”表示p等价于q,等价命题可以进行转换,当我们要证明p成立时,就可以去证明q成立.
(3)利用集合间的包含关系进行判断:如果条件p和结论q相应的集合分别为A和B,那么若A?B,则p是q的充分条件;若A?B,则p是q的必要条件;若A=B,则p是q的充分必要条件.
2.根据充分条件、必要条件求参数的取值范围时,主要根据充分条件、必要条件与集合间的关系,将问题转化为相应的两个集合之间的包含关系,然后建立关于参数的不等式(组)进行求解.本课结束
