人教版选修1-1 1.2.1充分条件与必要条件课件(18张)
文档属性
| 名称 | 人教版选修1-1 1.2.1充分条件与必要条件课件(18张) |

|
|
| 格式 | zip | ||
| 文件大小 | 343.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-20 23:07:54 | ||
图片预览






文档简介
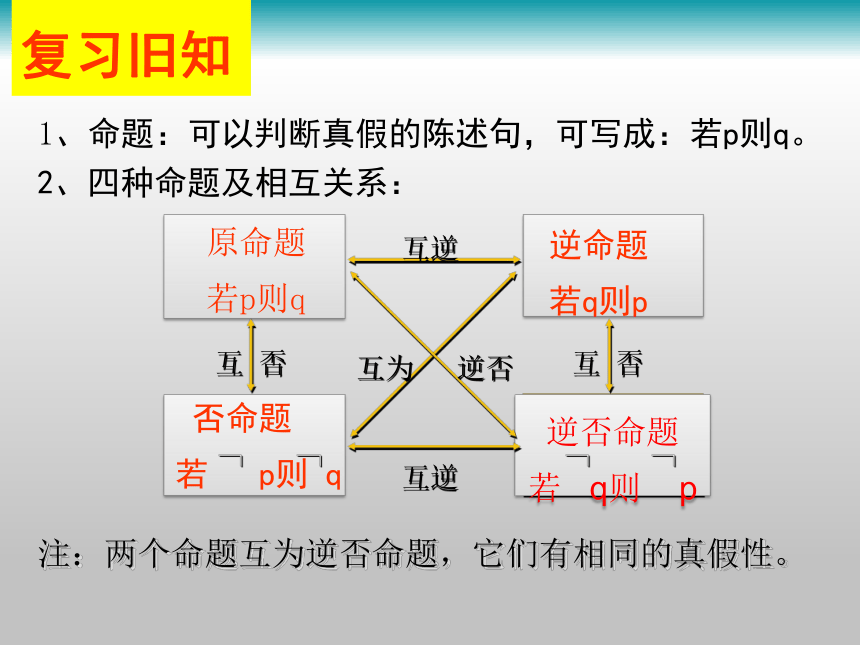
课件18张PPT。充分条件与必要条件注:两个命题互为逆否命题,它们有相同的真假性。复习旧知1、命题:可以判断真假的陈述句,可写成:若p则q。2、四种命题及相互关系:1、例 : 将(1)(2) (3)改写成“若p,则q”的形式 并判断下列命题的真假及逆命题的真假 。
(1)有两角相等的三角形是等腰三角形。
(2)若a2>b2,则a>b。
(3)能被4整除的数必是偶数;
解 (1)原命题:若一个三角形有两个角相等,则这个 三角形是等腰三角形。 (2)若a2>b2,则a>b。真命题
假命题(3)若某个整数能被4整除,则这个数必是偶数。真命题逆:真命题逆:假命题逆:假命题概念引入 早在战国时期,《墨经》中就有这样一段话“有之则必然,无之则未必不然,是为大故,无之则必不然,有之则未必然,是为小故”。
今天,在日常生活中,常听人说:“这充分说明……”,“没有这个必要”等,在数学中,也讲“充分”和“必要”,这节课,我们就来学习教材第一章第二节------充分条件与必要条件。 在语文中关联词有“只要……就……”,“只有……才……”等。创设情境 导入新课一般地:“若p,则q”为真,记作: 或“若p,则q”为假,记作:若两个三角形全等,则两三角形面积相等.例如:若两个三角形面积相等,则两三角形全等.合作探究 总结规律 充分条件与必要条件用符号 与 填空. (1) x2=y2 x=y; (2)内错角相等 两直线平行; (3) ac=bc a=b
(4)整数a能被6整除 a的个位数字为偶数; 学以致用 巩固提高要求:阅读下面问题,先独立完成,然后举手发言. 充分条件与必要条件:一般地,“若p则q”为真命题,是指由p通过推理可以得出q.这时,我们就说,由p可推出q,记作 ,并且说,p是q的充分条件,q是p的必要条件.例如:充分条件与必要条件合作探究 总结规律?充分必要充分必要合作探究 总结规律充分条件与必要条件例1 下列“若p,则q”形式的命题中,哪些命题中的p是q的充分条件?
(1)若x=1,则x2-4x+3=0;
(2)若f(x)=x,则f(x)在(-∞,+∞ )上为增函数;
(3)若x为无理数,则x2为无理数 .解:
命题(1)(2)是真命题,命题(3)是假命题.
所以,命题(1)(2)中的p是q的充分条件.学以致用 巩固提高 充分条件与必要条件下列条件中哪些是a+b>0的充分条件?a>0,b>0②a<0,b<0④a>0,b<0且|a|>|b|③a=3,b=-2特点:先给多个p,进行选择,通过选择,
感知p的不唯一性.
答案:① ③ ④【变式练习】学以致用 巩固提高 充分条件与必要条件例2 下列“若p,则q”形式的命题中,哪些命题中的q是p的必要条件?
(1)若x=y,则x2=y2;
(2)若x<3,则x<5;
(3)若a>b,则ac>bc.解:命题(1)(2)是真命题,命题(3)是假命题.
所以,命题(1)(2)中的q是p的必要条件.学以致用 巩固提高 充分条件与必要条件例3、已知p:-2≤x≤10,q:1-m≤x≤1+m(m>0).
(1)若p是q的必要不充分条件,求实数m的取值范围;
(2)若p是q的充分不必要条件,求实数m的取值范围.[解] (1)p:-2≤x≤10,q:1-m≤x≤1+m(m>0).
因为p是q的必要不充分条件,所以q是p的充分不必要条件又m>0,所以实数m的取值范围为{m|0<m≤3}.?所以m≥9,即实数m的取值范围是{m|m≥9}.?根据充分条件、必要条件求参数的取值范围时,可以先把p,q等价转化,利用充分条件、必要条件与集合间的包含关系,建立关于参数的不等式(组)进行求解. 注意:
已知 a,b,c,d 为实数,且 c>d ,“ a > b ”是“ a – c > b – d ”的( )
A. 充分条件 B. 必要条件
C. 充分不必要条件 D. 不必要条件B学以致用 巩固提高 充分条件与必要条件下列选项中,p不是q 的充分条件的是( )AA . p:a+c>b+d, q:a>b且c>d
B. p:a>1,b>1
q:f(x)=ax-b(a>0,且a≠1)的图像经过第二象限
C. p:x=1,q:x2=x
D. p:a>1,q:f(x)=log a x (a>0,且 a ≠1)在(0, +∞)为增函数.学以致用 巩固提高 充分条件与必要条件(3)利用集合间的包含关系进行判断:如果条件p和结论q相应的集合分别为A和B,那么若A?B,则p是q的充分条件;若A?B,则p是q的必要条件;若A=B,则p是q的充分必要条件.素养提炼:充分条件、必要条件的判断方法:(1)定义法:直接利用定义进行判断.(2)等价法:“p?q”表示p等价于q,等价命题可以进行转换,当我们要证明p成立时,就可以去证明q成立.2、方法收获
(1)判别步骤:
给出p,q 判断“p=>q”真假 下结论
(2)判别技巧
①否定命题时举反例②适时用逆否命题判断原命题真假
..一、生活中的一些名言警句包含着充要关系,
如:“骄兵必败”、“玉不琢,不成器”、
“若要人不知,除非己莫为”等等.请大家自
己试着找一些,分析其关系,感受数学的魅力.
二、完成课本作业布置
(3)能被4整除的数必是偶数;
解 (1)原命题:若一个三角形有两个角相等,则这个 三角形是等腰三角形。 (2)若a2>b2,则a>b。真命题
假命题(3)若某个整数能被4整除,则这个数必是偶数。真命题逆:真命题逆:假命题逆:假命题概念引入 早在战国时期,《墨经》中就有这样一段话“有之则必然,无之则未必不然,是为大故,无之则必不然,有之则未必然,是为小故”。
今天,在日常生活中,常听人说:“这充分说明……”,“没有这个必要”等,在数学中,也讲“充分”和“必要”,这节课,我们就来学习教材第一章第二节------充分条件与必要条件。 在语文中关联词有“只要……就……”,“只有……才……”等。创设情境 导入新课一般地:“若p,则q”为真,记作: 或“若p,则q”为假,记作:若两个三角形全等,则两三角形面积相等.例如:若两个三角形面积相等,则两三角形全等.合作探究 总结规律 充分条件与必要条件用符号 与 填空. (1) x2=y2 x=y; (2)内错角相等 两直线平行; (3) ac=bc a=b
(4)整数a能被6整除 a的个位数字为偶数; 学以致用 巩固提高要求:阅读下面问题,先独立完成,然后举手发言. 充分条件与必要条件:一般地,“若p则q”为真命题,是指由p通过推理可以得出q.这时,我们就说,由p可推出q,记作 ,并且说,p是q的充分条件,q是p的必要条件.例如:充分条件与必要条件合作探究 总结规律?充分必要充分必要合作探究 总结规律充分条件与必要条件例1 下列“若p,则q”形式的命题中,哪些命题中的p是q的充分条件?
(1)若x=1,则x2-4x+3=0;
(2)若f(x)=x,则f(x)在(-∞,+∞ )上为增函数;
(3)若x为无理数,则x2为无理数 .解:
命题(1)(2)是真命题,命题(3)是假命题.
所以,命题(1)(2)中的p是q的充分条件.学以致用 巩固提高 充分条件与必要条件下列条件中哪些是a+b>0的充分条件?a>0,b>0②a<0,b<0④a>0,b<0且|a|>|b|③a=3,b=-2特点:先给多个p,进行选择,通过选择,
感知p的不唯一性.
答案:① ③ ④【变式练习】学以致用 巩固提高 充分条件与必要条件例2 下列“若p,则q”形式的命题中,哪些命题中的q是p的必要条件?
(1)若x=y,则x2=y2;
(2)若x<3,则x<5;
(3)若a>b,则ac>bc.解:命题(1)(2)是真命题,命题(3)是假命题.
所以,命题(1)(2)中的q是p的必要条件.学以致用 巩固提高 充分条件与必要条件例3、已知p:-2≤x≤10,q:1-m≤x≤1+m(m>0).
(1)若p是q的必要不充分条件,求实数m的取值范围;
(2)若p是q的充分不必要条件,求实数m的取值范围.[解] (1)p:-2≤x≤10,q:1-m≤x≤1+m(m>0).
因为p是q的必要不充分条件,所以q是p的充分不必要条件又m>0,所以实数m的取值范围为{m|0<m≤3}.?所以m≥9,即实数m的取值范围是{m|m≥9}.?根据充分条件、必要条件求参数的取值范围时,可以先把p,q等价转化,利用充分条件、必要条件与集合间的包含关系,建立关于参数的不等式(组)进行求解. 注意:
已知 a,b,c,d 为实数,且 c>d ,“ a > b ”是“ a – c > b – d ”的( )
A. 充分条件 B. 必要条件
C. 充分不必要条件 D. 不必要条件B学以致用 巩固提高 充分条件与必要条件下列选项中,p不是q 的充分条件的是( )AA . p:a+c>b+d, q:a>b且c>d
B. p:a>1,b>1
q:f(x)=ax-b(a>0,且a≠1)的图像经过第二象限
C. p:x=1,q:x2=x
D. p:a>1,q:f(x)=log a x (a>0,且 a ≠1)在(0, +∞)为增函数.学以致用 巩固提高 充分条件与必要条件(3)利用集合间的包含关系进行判断:如果条件p和结论q相应的集合分别为A和B,那么若A?B,则p是q的充分条件;若A?B,则p是q的必要条件;若A=B,则p是q的充分必要条件.素养提炼:充分条件、必要条件的判断方法:(1)定义法:直接利用定义进行判断.(2)等价法:“p?q”表示p等价于q,等价命题可以进行转换,当我们要证明p成立时,就可以去证明q成立.2、方法收获
(1)判别步骤:
给出p,q 判断“p=>q”真假 下结论
(2)判别技巧
①否定命题时举反例②适时用逆否命题判断原命题真假
..一、生活中的一些名言警句包含着充要关系,
如:“骄兵必败”、“玉不琢,不成器”、
“若要人不知,除非己莫为”等等.请大家自
己试着找一些,分析其关系,感受数学的魅力.
二、完成课本作业布置
