人教版选修1-1 3.4生活中的优化问题举例课件(15张)
文档属性
| 名称 | 人教版选修1-1 3.4生活中的优化问题举例课件(15张) |

|
|
| 格式 | zip | ||
| 文件大小 | 323.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-22 00:00:00 | ||
图片预览






文档简介
课件15张PPT。3.4生活中的优化问题举例 生活中经常会遇到求什么条件下可使用料最省,利润最大,效率最高等问题,这些问题通常称为优化问题.
这往往可以归结为求函数的最大值或最小值问题.其中
不少问题可以运用导数这一有力工具加以解决.例1:海报版面尺寸的设计
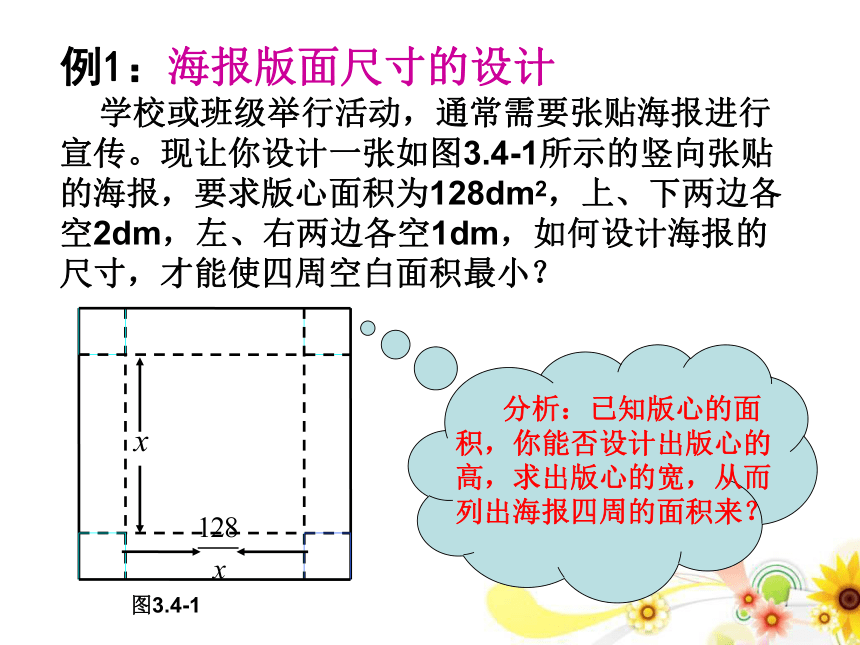
学校或班级举行活动,通常需要张贴海报进行宣传。现让你设计一张如图3.4-1所示的竖向张贴的海报,要求版心面积为128dm2,上、下两边各空2dm,左、右两边各空1dm,如何设计海报的尺寸,才能使四周空白面积最小?例1:海报版面尺寸的设计
学校或班级举行活动,通常需要张贴海报进行宣传。现让你设计一张如图3.4-1所示的竖向张贴的海报,要求版心面积为128dm2,上、下两边各空2dm,左、右两边各空1dm,如何设计海报的尺寸,才能使四周空白面积最小?图3.4-1解法一:由解法(一)得 因此,x=16是函数S(x)的极小值,也是最小值点。所以,当版心高为16dm,宽为8dm时,能使四周空白面积最小。 ∴函数在(0,16)上是减函数因此,当版心高为8dm,宽为16dm时,能使四周空白面积最小。解:设箱底边长为x,则箱高h=(60-x)/2.箱子容积
V(x)=x2h=(60x2-x3)/2(0若已知甲、乙两地相距100千米,求当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?解:设当汽车以x km/h的速度行驶时,从甲地到乙地
的耗油量为h(x) L,则答:当汽车以80千米/小时的速度匀速行驶时,从甲地到乙地耗油最少,最少为11.25升 小结 由上述例子,我们不难发现,解决优化问题的基本思路是:优化问题用函数表示的数学问题用导数解决数学问题优化问题的答案上述解决优化问题的过程是一个典型的数学建模过程。
这往往可以归结为求函数的最大值或最小值问题.其中
不少问题可以运用导数这一有力工具加以解决.例1:海报版面尺寸的设计
学校或班级举行活动,通常需要张贴海报进行宣传。现让你设计一张如图3.4-1所示的竖向张贴的海报,要求版心面积为128dm2,上、下两边各空2dm,左、右两边各空1dm,如何设计海报的尺寸,才能使四周空白面积最小?例1:海报版面尺寸的设计
学校或班级举行活动,通常需要张贴海报进行宣传。现让你设计一张如图3.4-1所示的竖向张贴的海报,要求版心面积为128dm2,上、下两边各空2dm,左、右两边各空1dm,如何设计海报的尺寸,才能使四周空白面积最小?图3.4-1解法一:由解法(一)得 因此,x=16是函数S(x)的极小值,也是最小值点。所以,当版心高为16dm,宽为8dm时,能使四周空白面积最小。 ∴函数在(0,16)上是减函数因此,当版心高为8dm,宽为16dm时,能使四周空白面积最小。解:设箱底边长为x,则箱高h=(60-x)/2.箱子容积
V(x)=x2h=(60x2-x3)/2(0
的耗油量为h(x) L,则答:当汽车以80千米/小时的速度匀速行驶时,从甲地到乙地耗油最少,最少为11.25升 小结 由上述例子,我们不难发现,解决优化问题的基本思路是:优化问题用函数表示的数学问题用导数解决数学问题优化问题的答案上述解决优化问题的过程是一个典型的数学建模过程。
