1.2.2 函数的表示法 第1课时 函数的表示法 31张
文档属性
| 名称 | 1.2.2 函数的表示法 第1课时 函数的表示法 31张 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-22 15:48:15 | ||
图片预览









文档简介
(共31张PPT)
1.2.2 函数的表示法
第1课时 函数的表示法
1.回顾初中函数的表示方法有哪些?
2
生活中函数的例子随处可见,例如某班某次考试成绩
表;由北京开往上海的各火车站与票价的对应表;边长为x的正方形田地的面积计算,以及在股市交易所中会经常见到的股票指数曲线图等.
想一想,生活中的这些函数实例,它们都是以什么
“面貌”呈现在我们面前的?通过本节课的学习,将会
有一个全新的认识.
1.掌握函数的三种表示法:解析法、列表法、图象法,体会三种表示方法的优点.(重点)
2.会求函数解析式,并正确画出函数的图象.
(难点)
探究点1 解析法
用数学表达式表示两个变量之间的对应关系的方法
优点: ①函数关系清楚、精确;②容易从自变量的值求出其对应的函数值;③便于研究函数的性质。解析法是中学研究函数的主要表达方法。
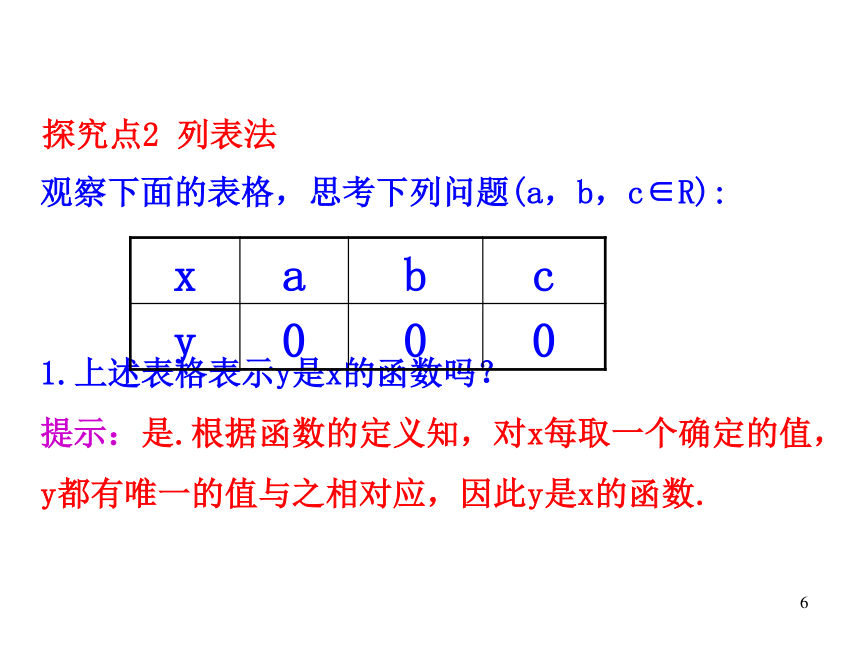
探究点2 列表法
观察下面的表格,思考下列问题(a,b,c∈R):
1.上述表格表示y是x的函数吗?
提示:是.根据函数的定义知,对x每取一个确定的值,y都有唯一的值与之相对应,因此y是x的函数.
x a b c
y 0 0 0
2.所有的函数都能用列表法来表示吗?
提示:并不是所有函数都能用列表法来表示,如函数y=2x+1,x∈R.因为自变量x∈R不能一一列出,所以不能用列表法来表示.
列出表格来表示两个变量之间的对应关系的方法.
如:平方表,平方根表,汽车、火车站的里程价目表、银行里的“利率表”等。
优点:不必通过计算就知道当自变量取某些值时函数的对应值,当自变量的值的个数较少时使用,列表法在实际生产和生活中有广泛的应用.
探究点3 图象法
用图象表示两个变量之间的对应关系的方法.
如:一次函数y=kx+b (k<0、b>0)的图象是一条直线;
优点:能形象直观地表示出函数的变化趋势,是今后利用数形结合思想解题的基础.
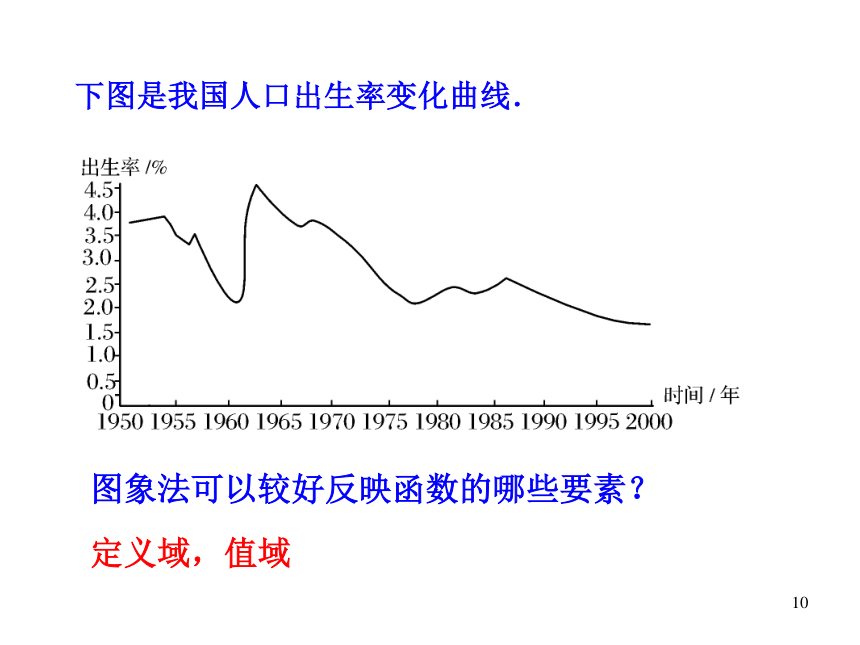
图象法可以较好反映函数的哪些要素?
定义域,值域
下图是我国人口出生率变化曲线.
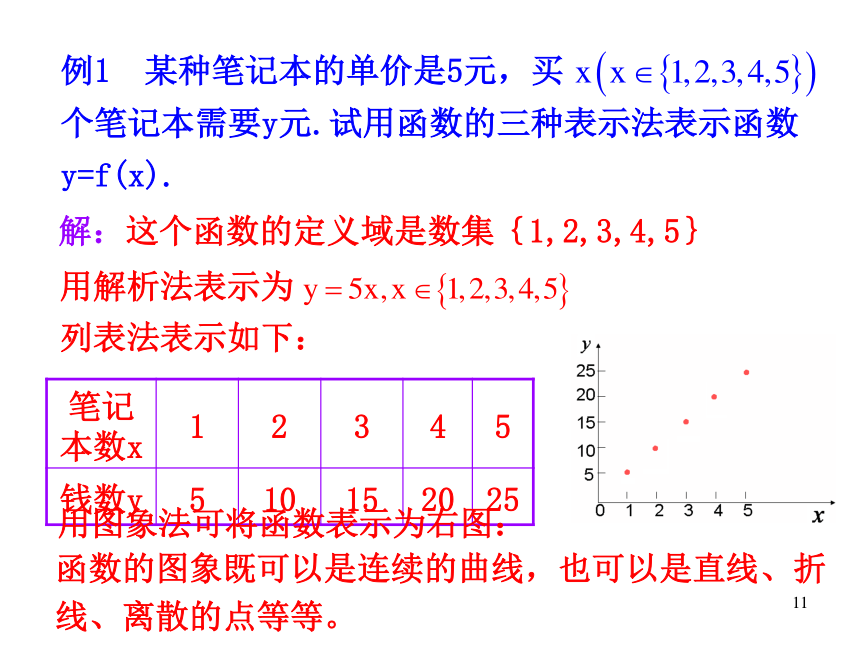
例1 某种笔记本的单价是5元,买 个笔记本需要y元.试用函数的三种表示法表示函数
y=f(x).
解:这个函数的定义域是数集{1,2,3,4,5}
列表法表示如下:
用图象法可将函数表示为右图:
用解析法表示为
函数的图象既可以是连续的曲线,也可以是直线、折线、离散的点等等。
笔记本数x 1 2 3 4 5
钱数y 5 10 15 20 25
(1)用解析法表示函数是否一定要写出自变量的取值范围?
(2)用描点法画函数图象的一般步骤是什么?
列表、描点、连线(视其定义域决定是否连线)
函数的定义域是函数存在的前提,写函数解析式的时候,一般要写出函数的定义域.
例2 下表是某校高一(1)班三名同学在高一学年度六次数学测试的成绩及班级平均分表.
请你对这三位同学在高一学年度的数学学习情况做一个分析.
测试
序号
成
绩
姓名
第1次 第2次 第3次 第4次 第5次 第6次
王伟 98 87 91 92 88 95
张城 90 76 88 75 86 80
赵磊 68 65 73 72 75 82
班级平均分 88.2 78.3 85.4 80.3 75.7 82.6
解:从表中可以知道每位同学在每次测试中的成绩,但不太容易分析每位同学的成绩变化情况.如果将“成绩”与“测试序号”之间的关系用函数图象表示出来,如下图,那么就能比较直观地看到成绩变化的情况.这对我们的分析很有帮助.
从图我们看到,王伟同学的数学学习成绩始终高于班级平均水平,学习情况比较稳定而且成绩优秀,张城同学的数学成绩不稳定,总是在班级平均水平上下波动,而且波动幅度较大,赵磊同学的数学学习成绩低于班级平均水平,但他的成绩曲线呈上升趋势,表明他的数学成绩在稳步提高。
作函数图象时应注意的事项:
(1)画函数图象时首先关注函数的定义域,即在定义域内作图;
(2)图象是实线或实点,定义域外的部分有时可用虚线来衬托整个图象;
(3)要标出某些关键点,例如图象的顶点、端点、与坐标轴的交点等.要分清这些关键点是实心点还是空心点.
【提升总结】
1. 画出下列函数的图象:
(1)
(2)
解:(1)
(2)
【变式练习】
2.某路公共汽车,行进的站数与票价关系如下表:
此函数关系除了用列表法表示之外,能否用其他方法表示?
解:
行进的站数x 1 2 3 4 5 6 7 8 9
票价y 0.5 0.5 0.5 1 1 1 1.5 1.5 1.5
把两个变量的函数关系,用一个等式来表示,这个等式就叫函数的解析式,简称解析式.
探究点4 求函数解析式
二、求函数解析式的常用方法有:
1.待定系数法
2.换元法(构造法)
3.消元法
一、函数的解析式:
例3 已知f(x)是一次函数,f(f(x))=4x-1,求
f(x)的解析式.
解:设f(x)=kx+b(k≠0)
则 f(f(x))=f(kx+b)=k(kx+b)+b
=k2x+kb+b=4x-1
待定系数法
适合:已知函数的模型(如一次函数、二次函数、反比例函数等)求函数解析式.
【变式练习】
例4 已知
,求
解:
适合:已知f(g(x))的解析式,求f(x).
换元法
例5 已知
,求
解:由
解得
消元法
适合: 同时含有
1.已知函数f(x)由表给出:
则f(2)的值为( )
A.4 B.2 C.0 D.1
D
x -1 0 1 2
f(x) 4 2 0 1
3.已知
求f(x)的解析式.
解:
1.函数的三种表示方法的优缺点比较
优点 缺点
解析法 一是简明、全面地概括了变量间的关系;二是通过解析式可以求出任意一个自变量所对应的函数值 不够形象、直观、具
体,而且并不是所有
的函数都能用解析式
表示出来
列表法 不需要计算就可以直接看出与自变量的值相对应的函数值 它只能表示自变量取
较少的有限值的对应
关系
2.函数的三种表示方法相互兼容和补充,许多函数是可以同时用这三种方法来表示的,但在实际操作中,仍以解析法和图象法为主.
图象法 能形象、直观地表示出函数的变化情况 只能近似地求出自变量的值所对应的函数值,而且有时误差较大
时间应分配得精密,使每年、每月、每日和每小时都有它的特殊任务。
1.2.2 函数的表示法
第1课时 函数的表示法
1.回顾初中函数的表示方法有哪些?
2
生活中函数的例子随处可见,例如某班某次考试成绩
表;由北京开往上海的各火车站与票价的对应表;边长为x的正方形田地的面积计算,以及在股市交易所中会经常见到的股票指数曲线图等.
想一想,生活中的这些函数实例,它们都是以什么
“面貌”呈现在我们面前的?通过本节课的学习,将会
有一个全新的认识.
1.掌握函数的三种表示法:解析法、列表法、图象法,体会三种表示方法的优点.(重点)
2.会求函数解析式,并正确画出函数的图象.
(难点)
探究点1 解析法
用数学表达式表示两个变量之间的对应关系的方法
优点: ①函数关系清楚、精确;②容易从自变量的值求出其对应的函数值;③便于研究函数的性质。解析法是中学研究函数的主要表达方法。
探究点2 列表法
观察下面的表格,思考下列问题(a,b,c∈R):
1.上述表格表示y是x的函数吗?
提示:是.根据函数的定义知,对x每取一个确定的值,y都有唯一的值与之相对应,因此y是x的函数.
x a b c
y 0 0 0
2.所有的函数都能用列表法来表示吗?
提示:并不是所有函数都能用列表法来表示,如函数y=2x+1,x∈R.因为自变量x∈R不能一一列出,所以不能用列表法来表示.
列出表格来表示两个变量之间的对应关系的方法.
如:平方表,平方根表,汽车、火车站的里程价目表、银行里的“利率表”等。
优点:不必通过计算就知道当自变量取某些值时函数的对应值,当自变量的值的个数较少时使用,列表法在实际生产和生活中有广泛的应用.
探究点3 图象法
用图象表示两个变量之间的对应关系的方法.
如:一次函数y=kx+b (k<0、b>0)的图象是一条直线;
优点:能形象直观地表示出函数的变化趋势,是今后利用数形结合思想解题的基础.
图象法可以较好反映函数的哪些要素?
定义域,值域
下图是我国人口出生率变化曲线.
例1 某种笔记本的单价是5元,买 个笔记本需要y元.试用函数的三种表示法表示函数
y=f(x).
解:这个函数的定义域是数集{1,2,3,4,5}
列表法表示如下:
用图象法可将函数表示为右图:
用解析法表示为
函数的图象既可以是连续的曲线,也可以是直线、折线、离散的点等等。
笔记本数x 1 2 3 4 5
钱数y 5 10 15 20 25
(1)用解析法表示函数是否一定要写出自变量的取值范围?
(2)用描点法画函数图象的一般步骤是什么?
列表、描点、连线(视其定义域决定是否连线)
函数的定义域是函数存在的前提,写函数解析式的时候,一般要写出函数的定义域.
例2 下表是某校高一(1)班三名同学在高一学年度六次数学测试的成绩及班级平均分表.
请你对这三位同学在高一学年度的数学学习情况做一个分析.
测试
序号
成
绩
姓名
第1次 第2次 第3次 第4次 第5次 第6次
王伟 98 87 91 92 88 95
张城 90 76 88 75 86 80
赵磊 68 65 73 72 75 82
班级平均分 88.2 78.3 85.4 80.3 75.7 82.6
解:从表中可以知道每位同学在每次测试中的成绩,但不太容易分析每位同学的成绩变化情况.如果将“成绩”与“测试序号”之间的关系用函数图象表示出来,如下图,那么就能比较直观地看到成绩变化的情况.这对我们的分析很有帮助.
从图我们看到,王伟同学的数学学习成绩始终高于班级平均水平,学习情况比较稳定而且成绩优秀,张城同学的数学成绩不稳定,总是在班级平均水平上下波动,而且波动幅度较大,赵磊同学的数学学习成绩低于班级平均水平,但他的成绩曲线呈上升趋势,表明他的数学成绩在稳步提高。
作函数图象时应注意的事项:
(1)画函数图象时首先关注函数的定义域,即在定义域内作图;
(2)图象是实线或实点,定义域外的部分有时可用虚线来衬托整个图象;
(3)要标出某些关键点,例如图象的顶点、端点、与坐标轴的交点等.要分清这些关键点是实心点还是空心点.
【提升总结】
1. 画出下列函数的图象:
(1)
(2)
解:(1)
(2)
【变式练习】
2.某路公共汽车,行进的站数与票价关系如下表:
此函数关系除了用列表法表示之外,能否用其他方法表示?
解:
行进的站数x 1 2 3 4 5 6 7 8 9
票价y 0.5 0.5 0.5 1 1 1 1.5 1.5 1.5
把两个变量的函数关系,用一个等式来表示,这个等式就叫函数的解析式,简称解析式.
探究点4 求函数解析式
二、求函数解析式的常用方法有:
1.待定系数法
2.换元法(构造法)
3.消元法
一、函数的解析式:
例3 已知f(x)是一次函数,f(f(x))=4x-1,求
f(x)的解析式.
解:设f(x)=kx+b(k≠0)
则 f(f(x))=f(kx+b)=k(kx+b)+b
=k2x+kb+b=4x-1
待定系数法
适合:已知函数的模型(如一次函数、二次函数、反比例函数等)求函数解析式.
【变式练习】
例4 已知
,求
解:
适合:已知f(g(x))的解析式,求f(x).
换元法
例5 已知
,求
解:由
解得
消元法
适合: 同时含有
1.已知函数f(x)由表给出:
则f(2)的值为( )
A.4 B.2 C.0 D.1
D
x -1 0 1 2
f(x) 4 2 0 1
3.已知
求f(x)的解析式.
解:
1.函数的三种表示方法的优缺点比较
优点 缺点
解析法 一是简明、全面地概括了变量间的关系;二是通过解析式可以求出任意一个自变量所对应的函数值 不够形象、直观、具
体,而且并不是所有
的函数都能用解析式
表示出来
列表法 不需要计算就可以直接看出与自变量的值相对应的函数值 它只能表示自变量取
较少的有限值的对应
关系
2.函数的三种表示方法相互兼容和补充,许多函数是可以同时用这三种方法来表示的,但在实际操作中,仍以解析法和图象法为主.
图象法 能形象、直观地表示出函数的变化情况 只能近似地求出自变量的值所对应的函数值,而且有时误差较大
时间应分配得精密,使每年、每月、每日和每小时都有它的特殊任务。
