1.2.2 函数的表示法 第2课时 分段函数及映射 25张
文档属性
| 名称 | 1.2.2 函数的表示法 第2课时 分段函数及映射 25张 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-22 15:50:53 | ||
图片预览








文档简介
(共25张PPT)
第2课时 分段函数及映射
只要你能把数报对,我就知道是什么牌
1.通过实例体会分段函数的概念.
2.会用分段函数解决简单的实际问题.(重点)
3.了解映射的概念及表示方法,并会判断一个对应关系是否是映射. (难点)
探究点1 分段函数
分段函数
有些函数在它的定义域中,对于自变量的
不同取值范围,对应关系不同,这种函数通常
称为_________.
分段函数
(1)分段函数是一个函数,不要把它误认为是几个函数;
注意
(2)分段函数的定义域是各段定义域的并集,值域是各段值域的并集.
1.求分段函数的函数值:
例1 已知函数f(x)=
x+2, x≤-1;
x2, -1<x<2;
2x, x≥2.
(2)若f(x)=3,求x的值.
(1)求 的值;
解:(1)
(2)
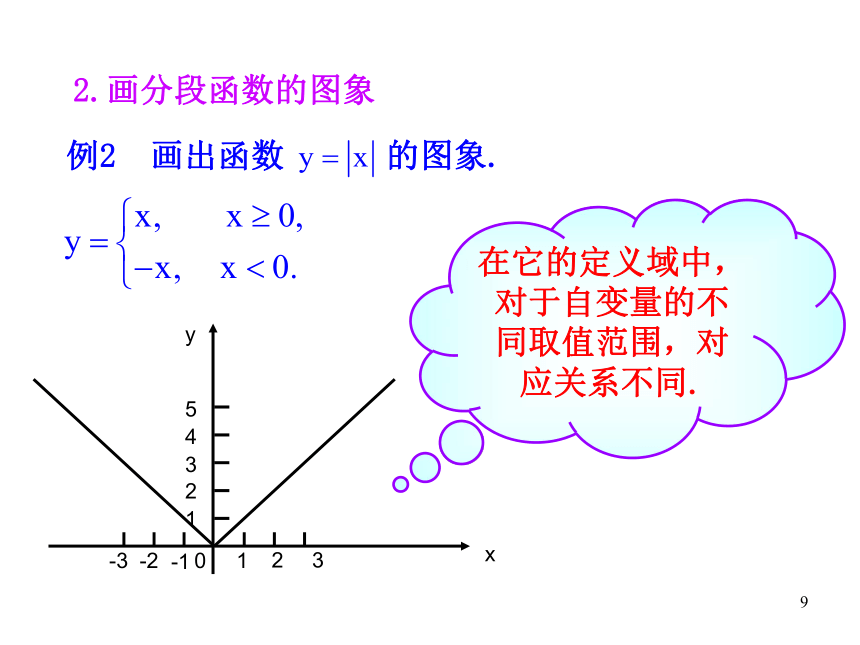
在它的定义域中,对于自变量的不同取值范围,对应关系不同.
例2 画出函数 的图象.
2.画分段函数的图象
例3 某市“招手即停”公共汽车的票价按下列规则制定:
(1)5公里以内(含5公里),票价2元;
(2)5公里以上,每增加5公里,票价增加1元(不足5公里的按5公里计算).
如果某条线路的总里程为20公里,请根据题意,
写出票价与里程之间的函数解析式,并画出函数的图象.
3.求分段函数的解析式
y=
2, 03, 5 < x ≤ 10
4, 10 < x ≤ 15
5, 15 < x≤20
解:设票价为y元,里程为x公里,由题意可知,自变量x
的取值范围是(0,20]
由“招手即停”公共汽车票价的制定规定,可得到以下
函数解析式:
根据这个函数解析式,
可画出函数图象,
如右图:
y
○
2
O
5
10
15
20
1
3
4
5
x
○
○
○
1.已知
求 的值.
解:
函数值作为自变量
【变式练习】
2.某质点在30s内运动速度vcm/s是时间t的函数,它的图象如右图,用解析式表示出这个函数.
解:v(t)=
t+10, (0 ≤ t<5)
3t,(5 ≤ t<10)
30,(10 ≤t <20)
-3t+90,(20 ≤ t≤30)
填写下图中的对应关系
A
B
(1)相应国家的首都
(2)求平方
(3)乘以2
x
x
x
2
x
2x
一对一
多对一
一对一
(1),(2),(3)的共同特征:集合A中的任何一个元素,在集合B中都有唯一的元素和它对应.
X的首都
1 2 3 4 5 6
1 2 3
A
B
探究点2 映射
一般地,设A、B是两个___________,如果按某一个确
定的对应关系f,使对于集合A中的_____一个元素x,在集
合B中都有_____确定的元素y与之对应,那么就称对应
f:A→B为从集合A到集合B的一个映射.
映射的概念
若对应是映射,必须满足两个条件:
①A中任何一个元素在B中都有元素与之对应.
②A在B中所对应的元素是唯一的.
注意
针对于集合A来说,不管集合B
非空的集合
任意
唯一
因此还可以用映射的概念来定义函数:
如果A、B是非空数集,那么A到B的映射f:A→B,
就叫做A到B的函数,
记作:y=f(x)
函数是一种特殊的映射
函数
映射
对应
例4 以下给出的对应是不是从集合A到B的映射?
(1)集合A={P|P是数轴上的点},集合B=R,对应关系
f:数轴上的点与它所代表的实数对应;
(2)集合A={P|P是平面直角坐标系中的点},集合B=
{(x,y)| x∈R,y∈R},对应关系f:平面直角坐标系
中的点与它的坐标对应;
(3)集合A={x|x是三角形},集合B={x|x是圆},对应
关系f:每一个三角形都对应它的内切圆;
(4)集合A={x|x是新华中学的班级},集合B={x|x是新
华中学的学生},对应关系f:每一个班级都对应班里的
学生.
是
不是
是
是
x
x
y
y
y
y
0
0
0
0
2
2
2
2
2
2
2
2
A.
1.设A=[0,2], B=[1,2], 在下列各图中,能表示
f:A→B的函数是( ).
D
x
x
B.
C.
D.
1
1
1
1
1
1
1
1
2.集合A={a,b,c},B={d,e},则从A到B可以建立
不同的映射个数为( )
A.5 B.6 C.8 D.9
【解析】逐一列出所有的映射为:
C
3.函数 的定义域是________.
【解析】分段函数的定义域是各段定义域的并集,所以此函数的定义域是[-2,3].
[-2,3]
4.某市居民自来水收费标准如下:每户每月用水不超过4吨为每吨1.80元,当用水超过4吨,超过部分每吨3.00元,某月甲、乙两户居民共缴水费y元,已知甲、乙两户的用水量分别为5x、3x(吨).
(1)求y关于x的函数;
(2)若甲、乙两户该月共缴水费26.40元,分别求出甲、乙两户该月的用水量和水费.
【解析】(1)依题意得y=
14.4x,0≤x≤ ,
20.4x-4.8, <x≤ ,
24x-9.6,x> .
(2)由于y=f(x)在各段区间上均单调递增,
当x∈[0, ]时,y≤f( )<26.4;
当x∈( , ]时,y≤f( )<26.4;
当x∈( ,+∞)时,令24x-9.6=26.4,得x=1.5.
所以甲用户的用水量为5x=7.5(吨),
缴水费4×1.8+3.5×3=17.7 (元),
乙用户用水量为3x=4.5(吨),
缴水费4×1.8+0.5×3=8.7(元).
1.分段函数
③“唯一性”:对于集合A中的任何一个元素,在集合B中和它对应的元素是唯一的.
①“有序性”:映射是有方向的,A到B的映射与B到A的映射往往不是同一个映射;
②“存在性”:对于集合A中的任何一个元素,集合B中都存在元素和它对应;
2.映射的“三性”
昨天是已经走过的,明天是即将走过的,惟有今天正在走过……
第2课时 分段函数及映射
只要你能把数报对,我就知道是什么牌
1.通过实例体会分段函数的概念.
2.会用分段函数解决简单的实际问题.(重点)
3.了解映射的概念及表示方法,并会判断一个对应关系是否是映射. (难点)
探究点1 分段函数
分段函数
有些函数在它的定义域中,对于自变量的
不同取值范围,对应关系不同,这种函数通常
称为_________.
分段函数
(1)分段函数是一个函数,不要把它误认为是几个函数;
注意
(2)分段函数的定义域是各段定义域的并集,值域是各段值域的并集.
1.求分段函数的函数值:
例1 已知函数f(x)=
x+2, x≤-1;
x2, -1<x<2;
2x, x≥2.
(2)若f(x)=3,求x的值.
(1)求 的值;
解:(1)
(2)
在它的定义域中,对于自变量的不同取值范围,对应关系不同.
例2 画出函数 的图象.
2.画分段函数的图象
例3 某市“招手即停”公共汽车的票价按下列规则制定:
(1)5公里以内(含5公里),票价2元;
(2)5公里以上,每增加5公里,票价增加1元(不足5公里的按5公里计算).
如果某条线路的总里程为20公里,请根据题意,
写出票价与里程之间的函数解析式,并画出函数的图象.
3.求分段函数的解析式
y=
2, 0
4, 10 < x ≤ 15
5, 15 < x≤20
解:设票价为y元,里程为x公里,由题意可知,自变量x
的取值范围是(0,20]
由“招手即停”公共汽车票价的制定规定,可得到以下
函数解析式:
根据这个函数解析式,
可画出函数图象,
如右图:
y
○
2
O
5
10
15
20
1
3
4
5
x
○
○
○
1.已知
求 的值.
解:
函数值作为自变量
【变式练习】
2.某质点在30s内运动速度vcm/s是时间t的函数,它的图象如右图,用解析式表示出这个函数.
解:v(t)=
t+10, (0 ≤ t<5)
3t,(5 ≤ t<10)
30,(10 ≤t <20)
-3t+90,(20 ≤ t≤30)
填写下图中的对应关系
A
B
(1)相应国家的首都
(2)求平方
(3)乘以2
x
x
x
2
x
2x
一对一
多对一
一对一
(1),(2),(3)的共同特征:集合A中的任何一个元素,在集合B中都有唯一的元素和它对应.
X的首都
1 2 3 4 5 6
1 2 3
A
B
探究点2 映射
一般地,设A、B是两个___________,如果按某一个确
定的对应关系f,使对于集合A中的_____一个元素x,在集
合B中都有_____确定的元素y与之对应,那么就称对应
f:A→B为从集合A到集合B的一个映射.
映射的概念
若对应是映射,必须满足两个条件:
①A中任何一个元素在B中都有元素与之对应.
②A在B中所对应的元素是唯一的.
注意
针对于集合A来说,不管集合B
非空的集合
任意
唯一
因此还可以用映射的概念来定义函数:
如果A、B是非空数集,那么A到B的映射f:A→B,
就叫做A到B的函数,
记作:y=f(x)
函数是一种特殊的映射
函数
映射
对应
例4 以下给出的对应是不是从集合A到B的映射?
(1)集合A={P|P是数轴上的点},集合B=R,对应关系
f:数轴上的点与它所代表的实数对应;
(2)集合A={P|P是平面直角坐标系中的点},集合B=
{(x,y)| x∈R,y∈R},对应关系f:平面直角坐标系
中的点与它的坐标对应;
(3)集合A={x|x是三角形},集合B={x|x是圆},对应
关系f:每一个三角形都对应它的内切圆;
(4)集合A={x|x是新华中学的班级},集合B={x|x是新
华中学的学生},对应关系f:每一个班级都对应班里的
学生.
是
不是
是
是
x
x
y
y
y
y
0
0
0
0
2
2
2
2
2
2
2
2
A.
1.设A=[0,2], B=[1,2], 在下列各图中,能表示
f:A→B的函数是( ).
D
x
x
B.
C.
D.
1
1
1
1
1
1
1
1
2.集合A={a,b,c},B={d,e},则从A到B可以建立
不同的映射个数为( )
A.5 B.6 C.8 D.9
【解析】逐一列出所有的映射为:
C
3.函数 的定义域是________.
【解析】分段函数的定义域是各段定义域的并集,所以此函数的定义域是[-2,3].
[-2,3]
4.某市居民自来水收费标准如下:每户每月用水不超过4吨为每吨1.80元,当用水超过4吨,超过部分每吨3.00元,某月甲、乙两户居民共缴水费y元,已知甲、乙两户的用水量分别为5x、3x(吨).
(1)求y关于x的函数;
(2)若甲、乙两户该月共缴水费26.40元,分别求出甲、乙两户该月的用水量和水费.
【解析】(1)依题意得y=
14.4x,0≤x≤ ,
20.4x-4.8, <x≤ ,
24x-9.6,x> .
(2)由于y=f(x)在各段区间上均单调递增,
当x∈[0, ]时,y≤f( )<26.4;
当x∈( , ]时,y≤f( )<26.4;
当x∈( ,+∞)时,令24x-9.6=26.4,得x=1.5.
所以甲用户的用水量为5x=7.5(吨),
缴水费4×1.8+3.5×3=17.7 (元),
乙用户用水量为3x=4.5(吨),
缴水费4×1.8+0.5×3=8.7(元).
1.分段函数
③“唯一性”:对于集合A中的任何一个元素,在集合B中和它对应的元素是唯一的.
①“有序性”:映射是有方向的,A到B的映射与B到A的映射往往不是同一个映射;
②“存在性”:对于集合A中的任何一个元素,集合B中都存在元素和它对应;
2.映射的“三性”
昨天是已经走过的,明天是即将走过的,惟有今天正在走过……
