第二章 点、直线、平面之间的位置关系(立体几何小题专练)AB卷 解析版
文档属性
| 名称 | 第二章 点、直线、平面之间的位置关系(立体几何小题专练)AB卷 解析版 |  | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-20 17:13:27 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
A卷
1.如图所示,定点A和B都在平面α内,定点P?α,PB⊥α,C是平面α内异于A和B的动点,且PC⊥AC,则△ABC为 ( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.无法确定
【答案】B
【解析】因为PB⊥α,AC?α,所以PB⊥AC,
又AC⊥PC,PB∩PC=P,
所以AC⊥平面PBC,又BC?平面PBC,
所以AC⊥BC.故△ABC为直角三角形.
2.在正方体中,分别为,的中点,为侧面的中心,则异面直线与所成角的余弦值为
A. B. C. D.
【答案】A
【详解】
如图,以为坐标原点,分别以所在直线为轴建立空间直角坐标系. 设正方体的棱长为,则, ∴. 则. ∴异面直线与所成角的余弦值为 ,故选:A.
3.已知异面直线,所成的角为,直线与,均垂直,且垂足分别为,,若动点在直线上运动,动点在直线上运动,,则线段的中点的轨迹所围成的平面区域的面积是( )
A.9 B.18 C.36 D.72
【详解】
设AB的中点为,过作AB的垂面,则PQ的中点M必在平面内,
设PA,QB在平面内的射影为在上的射影为,
则,且,
以为原点,以为坐标轴在平面内建立平面直角坐标系,
设,则,所以,即,
即点M的轨迹为菱形,且菱形轨迹所围成的区域的面积为,故选B.
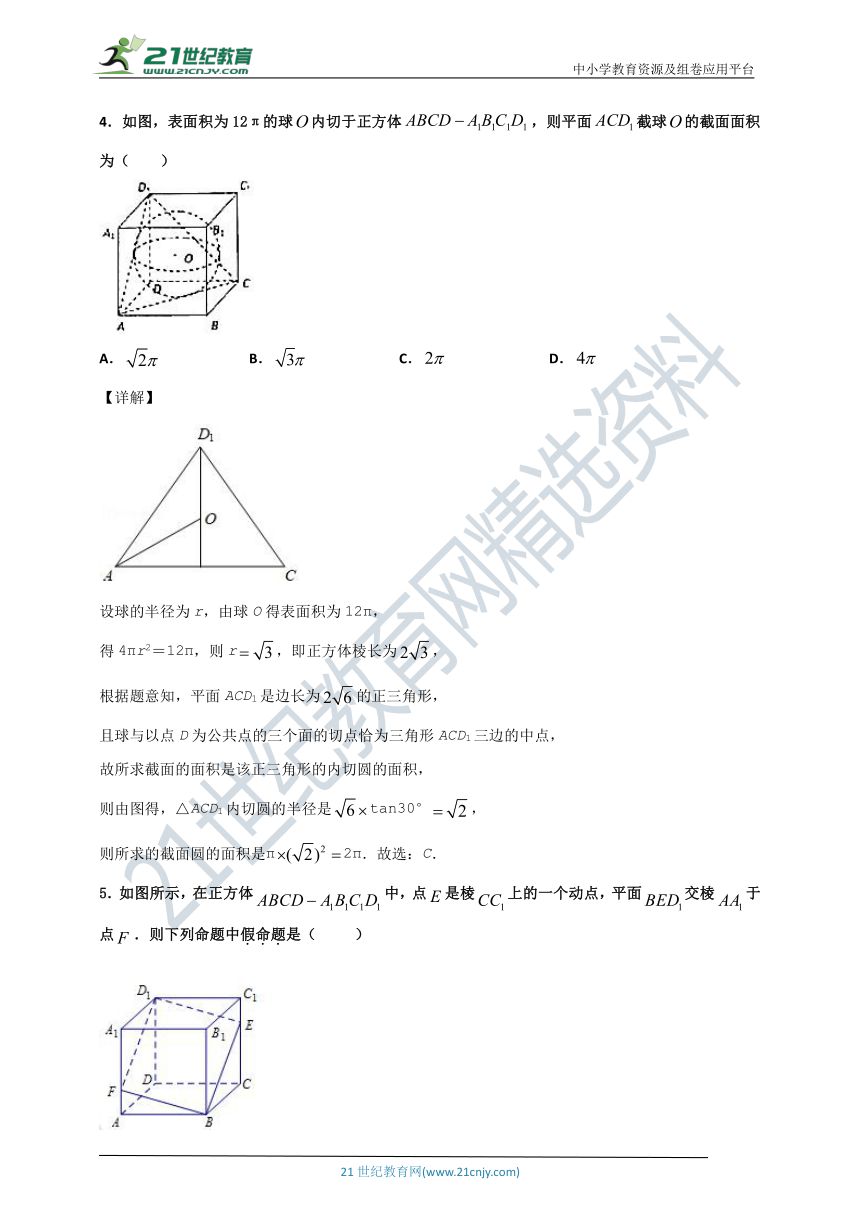
4.如图,表面积为12π的球内切于正方体,则平面截球的截面面积为( )
A. B. C. D.
【详解】
设球的半径为r,由球O得表面积为12π,
得4πr2=12π,则r,即正方体棱长为,
根据题意知,平面ACD1是边长为的正三角形,
且球与以点D为公共点的三个面的切点恰为三角形ACD1三边的中点,
故所求截面的面积是该正三角形的内切圆的面积,
则由图得,△ACD1内切圆的半径是tan30°,
则所求的截面圆的面积是π2π.故选:C.
5.如图所示,在正方体中,点是棱上的一个动点,平面交棱于点.则下列命题中假命题是( )
(A)存在点,使得//平面
(B)存在点,使得平面
(C)对于任意的点,平面平面
(D)对于任意的点,四棱锥的体积均不变
【答案】B
【解析】
试题分析:当点为的中点时,由对称性可知也是的中点,此时//,因为,,所以//,故A正确;
假设,因为,所以。所以四边形为菱形或正方形,即。因为为正方体所以。所以假设不成立。故B不正确。
因为为正方形,所以,因为,,所以,因为,所以。因为,所以。同理可证,因为,所以,因为,所以。故C正确。
设正方体边长为,则。故D正确。
6.如图,已知正三棱锥,,,点,分别在核,上(不包含端点),则直线,所成的角的取值范围是_________.
【详解】
如下图所示:
过点作平面,垂足为点,则点为等边的中心,
由正弦定理得,
平面,易得,
当点在线段上运动时,直线与平面内的直线所成角的最小值,
即为直线与平面所成的角,设这个角为,则,
显然,当点位于棱的端点时,取最小值,此时,,则;
当点位于棱的中点时,则点位于线段上,且,
过点作交于点,
平面,平面,则,
又,,平面,
平面,,此时,直线与所成的角取得最大值。
由于点不与棱的端点重合,所以,直线与所成角的取值范围是。
故答案为:。
7.四棱锥中,底面是边长为的正方形,其它四个侧面都是侧棱长为的等腰三角形,则二面角的度数为___________.
【详解】
如图所示,
由题意可得:四棱锥V-ABCD是正四棱锥,连接AC,BD,相交于点O,连接VO,则VO⊥平面ABCD.
取AB的中点M,连接VM,OM.则AB⊥OM,AB⊥VM.
∴∠OMV是二面角V-AB-C的平面角.
由底面是边长为的正方形可得:,
,
在中,.
即二面角的度数为.
8.如图,已知正方体ABCD-A1B1C1D1的棱长为1,E,F分别是棱AD,B1C1上的动点,设AE=λ,B1F=μ.若平面BEF与正方体的截面是五边形,则λ+μ的取值范围是________.
【详解】
由题意,当=1,=0,则平面BEF与正方体的截面是四边形,随着B1F=变大,平面BEF与正方体的截面是五边形,由此λ+μ>1, 随着B1F=,平面BEF与正方体的截面还是五边形,当==1,则平面BEF与正方体的截面是三角形,由此λ+μ<2,.
故1<λ+μ<2
故答案为:1<λ+μ<2.
9.如图所示,平面平面,,四边形为正方形,且,则异面直线与所成角的余弦值为__________.
【详解】
由题目中的位置关系,可将原图补为如图所示的直四棱柱:
异面直线与所成角即为直线与所成角
由余弦定理可得:
,又
.
本题正确结果:
B卷
10.在长方体中,,,若棱上存在点,使得,则棱的长的取值范围是__________.
【解析】
如图所示,当时,以为直径的圆与有交点,连接,则,底面,根据三垂线定理,则,满足题意,即棱的长的取值范围是,故答案为.
11.已知四面体中,,,分别为,的中点,且异面直线与所成的角为,则____.
【详解】
取BD中点O,连结EO、FO,
∵四面体ABCD中,AB=CD=2,E、F分别为BC、AD的中点,且异面直线AB与CD所成的角为,
∴EO∥CD,且EO,FO∥AB,且FO1,
∴∠EOF是异面直线AB与CD所成的角或其补角,
∴,或,
当∠EOF时,△EOF是等边三角形,∴EF=1.
当时,EF.
故答案为:1或.
12.如图,矩形中,,⊥平面,若在上只有一个点满足,则的值等于________.
解:连接AQ,取AD的中点O,连接OQ.
∵PA⊥平面ABCD,PQ⊥DQ,
∴由三垂线定理的逆定理可得DQ⊥AQ.
∴点Q在以线段AD的中点O为圆心的圆上,
又∵在BC上有且仅有一个点Q满足PQ⊥DQ,∴BC与圆O相切,(否则相交就有两点满足垂直,矛盾.)
∴OQ⊥BC,
∵AD∥BC,∴OQ=AB=1,∴BC=AD=2,
即a=2.
故答案为:2.
13.正方体为棱长为1,动点分别在棱上,过点的平面截该正方体所得的截面记为,设其中,下列命题正确的是
(写出所有正确命题的编号)________.
①当时,为矩形,其面积最大为1;
②当时,为等腰梯形;
③当时,为六边形;
④当时,设与棱的交点为,则.
【答案】②③④
对于①,当x=0时,过点A,P,Q的截面S是矩形,其面积最大是所以①错误;
对于②,当时,如图(2)所示,过点A,P,Q的截面S是等腰梯形,∴②正确;
对于③,当时,设S与棱的交点为R,如图(2),
延长,使,连接AN交于S,连接SR,
可得,,
可得,,∴③正确;④当y=1时,以B1为顶点,S为底面的棱锥如图(4)所示,
该四棱锥的体积为∴④正确.
14.已知二面角—l—为60°,若平面内有一点A到平面的距离为,那么A在平面内的射影B到平面的距离为____________.
【答案】
【解析】如图,由题意知, ,则,根据面积等积法,A在平面内的射影B到平面的距离为,故填.
15.如图,在直三棱柱ABC﹣A1B1C1中,AB=BC=AA1,∠ABC=90°,则直线AB1和BC1所成的角是 .
解:不妨设AB=BC=AA1=a,由题意可补成棱长为a的正方体,(如图)
∵AD1∥BC1,∴∠B1AD1就是直线AB1和BC1所成的角,
在正三角形AB1D1中易得∠B1AD1=60
故答案为:60°
16.直三棱柱中,若,,则异面直线与所成的角的余弦值等于
【答案】
【解析】
试题分析:以A为原点,AB为x轴,AC为y轴,为z轴,建立空间直角坐标系,设2AB=2AC==2,
则(0,0,2),B(1,0,0),(1,0,2),C(0,1,0),=(-1,0,2),=(-1,1,-2),
设异面直线与所成的角为θ,则
17.如图长方体中,,则二面角的大小为( )
A. B. C. D.
【答案】
【解析】
试题分析:因为,所以取BD的中点O,连,则即为二面角的一个平面角,由=,tan=知= 300,故选A。
18.如图,在正方体ABCD-A1B1C1D1中,有下面结论:
①AC∥平面CB1D1;
②AC1⊥平面CB1D1;
③AC1与底面ABCD所成角的正切值是;
④AD1与BD为异面直线.其中正确的结论的序号是________.
【答案】②③④
【详解】
①因为AC∩平面CB1D1=C,所以AC∥平面CB1D1错误,所以①错误.
②连结BC1,A1 C1,则BC1⊥B1 C,又因为AB⊥面BC C1B1
故 AB⊥B1 C, AB∩BC1=B,故B1 C⊥面ABC1
进而得到AC1⊥B1C,
连接A1 C1,同理可证B1D1⊥AC1
又因为B1D1∩B1 C于点B1
故得到AC1⊥平面CB1D1
所以②正确.
③因为AC1在底面ABCD的射影为AC,所以∠C1AC是AC1与底面ABCD所成的角,设正方体的边长为a,则AC=
所以所以③正确.
④由异面直线的定义可知,AD1与BD为异面直线,所以④正确.
故答案为:②③④.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
