北师大版高中数学必修二第二章第二节 直线与圆的位置关系(共24张PPT)
文档属性
| 名称 | 北师大版高中数学必修二第二章第二节 直线与圆的位置关系(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-22 16:13:07 | ||
图片预览







文档简介
(共24张PPT)
第二章 解析几何初步
高中数学必修2·精品课件
第2节第3课时 直线与圆的位置关系
学习目标
1.理解直线和圆的三种位置关系.(重点)
2.会用圆心到直线的距离来判断直线与圆的位置关系.(重点)
3.能解决直线与圆位置关系的综合问题.(易错点、难点)
知识清单
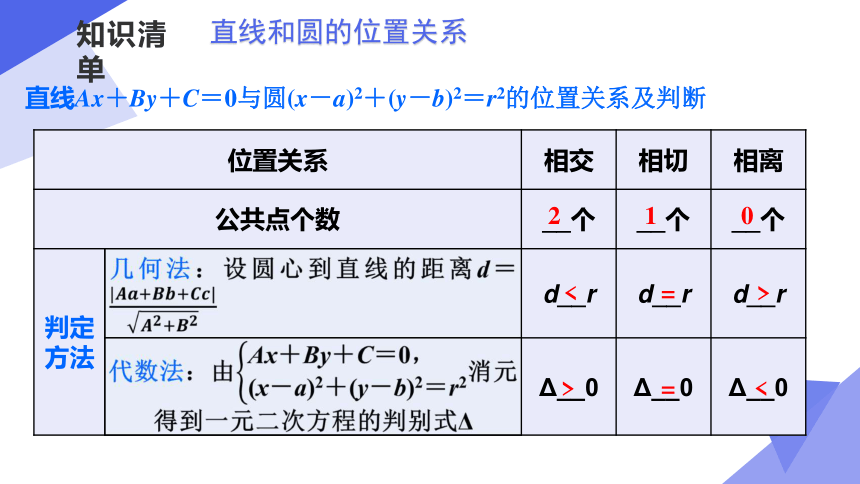
直线和圆的位置关系
位置关系 相交 相切 相离
公共点个数 __个 __个 __个
判定方法 d__r d__r d__r
Δ__0 Δ__0 Δ__0
直线Ax+By+C=0与圆(x-a)2+(y-b)2=r2的位置关系及判断
2
1
0
<
=
>
>
=
<
合作探究
直线和圆的位置关系
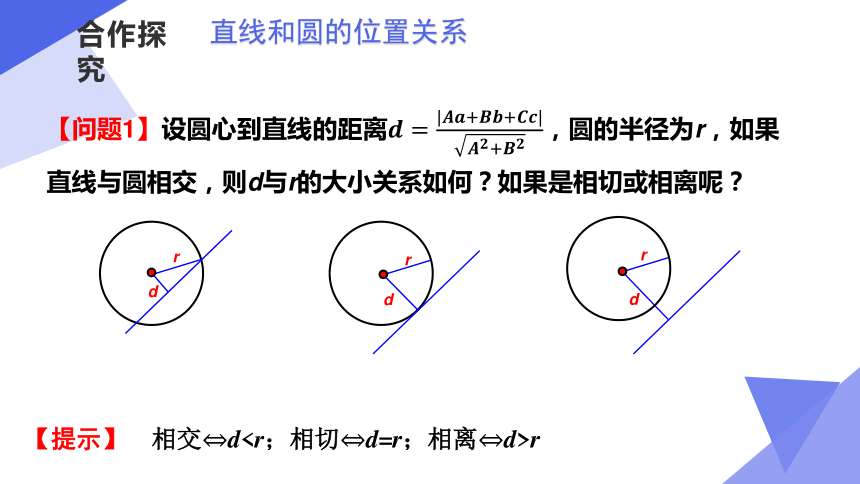
【问题1】设圆心到直线的距离,圆的半径为r,如果直线与圆相交,则d与r的大小关系如何?如果是相切或相离呢?
【提示】 相交?dr
d
r
d
r
r
d
合作探究
直线和圆的位置关系
【问题2】若直线方程为Ax+By+C=0,圆的方程为(x-a)2+(y-b)2=r2,设联立方程消元后得到的一元二次方程的判别式为Δ,如果直线和圆相交,那么上述一元二次方程有几个实数解?此时Δ满足什么条件?如果是相切或相离呢?
【提示】 相交?方程有2个不同实数解? Δ>0;
相切?方程有2个相同实数解? Δ=0;
相离?方程没有实数解? Δ<0.
典例精讲:题型一:直线与圆的位置关系的判定
例1:已知直线l:3x+y-6=0和圆C:x2+y2-2y-4=0,判断直线l与圆C的位置关系;如果相交,求出它们交点的坐标.
解:方法一:由直线与圆的方程得方程组
消去y,得x2-3x+2=0.
∵Δ=(-3)2-4×1×2=1>0,
∴直线与圆相交,有两个交点.
由方程组解得交点坐标为(2,0),(1,3).
典例精讲:题型一:直线与圆的位置关系的判定
解:方法二:圆的方程可化为x2+(y-1)2=5,其圆心为(0,1),半径为.圆心到直线l的距离为d,
∴直线与圆相交,有两个交点.
由直线与圆的方程得方程组
解得交点坐标为(2,0),(1,3).
题后反思
如果仅判断直线和圆的位置关系,则可直接利用方法二(几何法),即比较圆心到直线的距离和圆的半径的大小;如果需要求解直线和圆的交点,则应该利用方法一(代数法),即解由直线方程和圆的方程组成的方程组.
典例精讲:题型二:直线与圆相切问题
(1)求与圆x2+y2=13相切于点P(-3,2)的切线方程;
(2)求过点(2,-3)和圆(x-1)2+(y-1)2=1相切的直线方程.
例2:
分析:对于(1)注意到P点为切点,故可利用切线的性质解题,对于(2)由于(2,-3)不在圆上,可设出切线方程,将直线与圆联立,消元后得到的二次方程只有一个解,利用判别式求解,也可以利用圆心到直线的距离等于半径求解.
典例精讲:题型二:直线与圆相切问题
(1)解法1:显然切线的斜率存在,
设所求的切线方程为y-2=k(x+3),
即kx-y+3k+2=0,
由题意,得=,得k=.
故所求的切线方程为y-2=(x+3),即3x-2y+13=0.
解析:
典例精讲:题型二:直线与圆相切问题
(1)解法2:∵x2+y2=13的圆心为O(0,0),
∴kOP==-.
∴所求的切线的斜率k=-=.
故所求切线的方程为y-2=(x+3).
即3x-2y+13=0.
解析:
典例精讲:题型二:直线与圆相切问题
(1)解法3:∵(-3,2)在圆x2+y2=13上,
∴切线方程为-3x+2y=13.
即3x-2y+13=0.
解析:
典例精讲:题型二:直线与圆相切问题
(2)解法1:设所求的直线为x=2,或y+3=k(x-2).
当l为x=2时,圆心(1,1)到x=2的距离d=2-1=1符合题意.
当l为y+3=k(x-2),即kx-y-2k-3=0时,
由题意,得=1,得k=-.
∴切线方程为15x+8y-6=0.
综上得所求切线的方程为x=2,或15x+8y-6=0.
解析:
典例精讲:题型二:直线与圆相切问题
(2)解法2:设切点D(x0,y0),则切线方程为(x0-1)(x-1)+(y0-1)(y-1)=1,由题意,得
由②得x0=4y0-2,代入①得(4y0-3)2+(y0-1)2=1.
得17y02-26y0+9=0,得y0=1,或y0=.
∴切点坐标为(2,1)或(, ).
故切线方程为x=2,或15x+8y-6=0.
解析:
题后反思:
(1)由于过某一定点的直线有两类:斜率存在,斜率不存在,故过某一点做圆的切线,求切线方程时要分情况讨论.
(2)求切线一般有三种方法:①设切点坐标用切线公式:过圆(x-a)2+(y-b)2=r2上一点(x0,y0)的切线方程为(x-a)(x0-a)+(y0-b)(y-b)=r2;②设切线方程,用判别式法;③设切线方程,用圆心到切线的距离等于半径,但要注意斜率不存在的情况.
典例精讲:题型三:弦长问题
例3 过点P(4,-4)的直线l被圆C:x2+y2-2x-4y-20=0截得的弦AB的长度为8,求直线l的方程.
分析:设出直线l的方程,由圆心到直线的距离d与圆的半径及半弦长构成直角三角形求解.注意讨论斜率存在与否.
典例精讲:题型三:弦长问题
解:∵圆C的方程可化为(x-1)2+(y-2)2=52,
∴圆心的坐标为C(1,2),半径r=5.
由圆的性质可知圆的半弦长、半径、弦心距构成直角三角形,
圆心到直线的距离d==3.
当直线AB⊥x轴时,
∵直线l过点P(4,-4),
∴AB的方程为x=4,点C(1,2)到l的距离d=|4-1|=3,满足题意.
典例精讲:题型三:弦长问题
当AB与x轴不垂直时,设方程为y+4=k(x-4)(k≠0),即kx-y-4k-4=0.∵d==3,解得k=-.
∴l的方程为y+4=-(x-4),
即3x+4y+4=0.
综上,直线l的方程为x=4或3x+4y+4=0.
规律方法
求直线与圆相交时弦长的两种方法:
(1)几何法:如图,直线l与圆C交于A,B两点,设弦心距为d,圆的半径为r,弦长为|AB|,则有()2+d2=r2.即|AB|=2.
规律方法
(2)代数法:如图所示,将直线方程与圆的方程联立,设直线与圆的两交点分别是A(x1,y1),B(x2,y2),则|AB|=
=|x1-x2|=·|y1-y2|,其中k为直线l的斜率.
l
A(x1,y1)
B(x2,y2)
课堂练习
1.直线x-y-4=0与圆x2+y2-2x-2y-2=0的位置关系是( )
A.相交但直线不过圆心
B.相切
C.相交且直线过圆心
D.相离
D
课堂练习
2.求斜率为-且与圆x2+y2=16相切的直线方程.
解:设切线方程为y=-x+b,
即2x+3y-3b=0.已知圆的圆心为(0,0),半径r=4,则圆心到切线的距离d==4.解得b=±.故所求切线方程为2x+3y+4=0或2x+3y-4=0.
课堂练习
3.直线x+y-2=0截圆x2+y2=4得到的弦长为( )
B
解析:圆心到直线的距离d==1,
又r=2,所以弦长为2=2.
答案:B
A.1 B.2 C.2 D.2
归纳小结
1.判断直线与圆位置关系的途径主要有两个:一是圆心到直线的距离与圆的半径进行大小比较;二是直线与圆的方程组成的方程组解的个数.两者相比较,前者较形象、直观,便于运算.
2.与圆有关的弦长、切线问题常利用几何法求解,但注意验证所求直线的斜率不存在的情形,避免漏解.
第二章 解析几何初步
高中数学必修2·精品课件
第2节第3课时 直线与圆的位置关系
学习目标
1.理解直线和圆的三种位置关系.(重点)
2.会用圆心到直线的距离来判断直线与圆的位置关系.(重点)
3.能解决直线与圆位置关系的综合问题.(易错点、难点)
知识清单
直线和圆的位置关系
位置关系 相交 相切 相离
公共点个数 __个 __个 __个
判定方法 d__r d__r d__r
Δ__0 Δ__0 Δ__0
直线Ax+By+C=0与圆(x-a)2+(y-b)2=r2的位置关系及判断
2
1
0
<
=
>
>
=
<
合作探究
直线和圆的位置关系
【问题1】设圆心到直线的距离,圆的半径为r,如果直线与圆相交,则d与r的大小关系如何?如果是相切或相离呢?
【提示】 相交?d
d
r
d
r
r
d
合作探究
直线和圆的位置关系
【问题2】若直线方程为Ax+By+C=0,圆的方程为(x-a)2+(y-b)2=r2,设联立方程消元后得到的一元二次方程的判别式为Δ,如果直线和圆相交,那么上述一元二次方程有几个实数解?此时Δ满足什么条件?如果是相切或相离呢?
【提示】 相交?方程有2个不同实数解? Δ>0;
相切?方程有2个相同实数解? Δ=0;
相离?方程没有实数解? Δ<0.
典例精讲:题型一:直线与圆的位置关系的判定
例1:已知直线l:3x+y-6=0和圆C:x2+y2-2y-4=0,判断直线l与圆C的位置关系;如果相交,求出它们交点的坐标.
解:方法一:由直线与圆的方程得方程组
消去y,得x2-3x+2=0.
∵Δ=(-3)2-4×1×2=1>0,
∴直线与圆相交,有两个交点.
由方程组解得交点坐标为(2,0),(1,3).
典例精讲:题型一:直线与圆的位置关系的判定
解:方法二:圆的方程可化为x2+(y-1)2=5,其圆心为(0,1),半径为.圆心到直线l的距离为d,
∴直线与圆相交,有两个交点.
由直线与圆的方程得方程组
解得交点坐标为(2,0),(1,3).
题后反思
如果仅判断直线和圆的位置关系,则可直接利用方法二(几何法),即比较圆心到直线的距离和圆的半径的大小;如果需要求解直线和圆的交点,则应该利用方法一(代数法),即解由直线方程和圆的方程组成的方程组.
典例精讲:题型二:直线与圆相切问题
(1)求与圆x2+y2=13相切于点P(-3,2)的切线方程;
(2)求过点(2,-3)和圆(x-1)2+(y-1)2=1相切的直线方程.
例2:
分析:对于(1)注意到P点为切点,故可利用切线的性质解题,对于(2)由于(2,-3)不在圆上,可设出切线方程,将直线与圆联立,消元后得到的二次方程只有一个解,利用判别式求解,也可以利用圆心到直线的距离等于半径求解.
典例精讲:题型二:直线与圆相切问题
(1)解法1:显然切线的斜率存在,
设所求的切线方程为y-2=k(x+3),
即kx-y+3k+2=0,
由题意,得=,得k=.
故所求的切线方程为y-2=(x+3),即3x-2y+13=0.
解析:
典例精讲:题型二:直线与圆相切问题
(1)解法2:∵x2+y2=13的圆心为O(0,0),
∴kOP==-.
∴所求的切线的斜率k=-=.
故所求切线的方程为y-2=(x+3).
即3x-2y+13=0.
解析:
典例精讲:题型二:直线与圆相切问题
(1)解法3:∵(-3,2)在圆x2+y2=13上,
∴切线方程为-3x+2y=13.
即3x-2y+13=0.
解析:
典例精讲:题型二:直线与圆相切问题
(2)解法1:设所求的直线为x=2,或y+3=k(x-2).
当l为x=2时,圆心(1,1)到x=2的距离d=2-1=1符合题意.
当l为y+3=k(x-2),即kx-y-2k-3=0时,
由题意,得=1,得k=-.
∴切线方程为15x+8y-6=0.
综上得所求切线的方程为x=2,或15x+8y-6=0.
解析:
典例精讲:题型二:直线与圆相切问题
(2)解法2:设切点D(x0,y0),则切线方程为(x0-1)(x-1)+(y0-1)(y-1)=1,由题意,得
由②得x0=4y0-2,代入①得(4y0-3)2+(y0-1)2=1.
得17y02-26y0+9=0,得y0=1,或y0=.
∴切点坐标为(2,1)或(, ).
故切线方程为x=2,或15x+8y-6=0.
解析:
题后反思:
(1)由于过某一定点的直线有两类:斜率存在,斜率不存在,故过某一点做圆的切线,求切线方程时要分情况讨论.
(2)求切线一般有三种方法:①设切点坐标用切线公式:过圆(x-a)2+(y-b)2=r2上一点(x0,y0)的切线方程为(x-a)(x0-a)+(y0-b)(y-b)=r2;②设切线方程,用判别式法;③设切线方程,用圆心到切线的距离等于半径,但要注意斜率不存在的情况.
典例精讲:题型三:弦长问题
例3 过点P(4,-4)的直线l被圆C:x2+y2-2x-4y-20=0截得的弦AB的长度为8,求直线l的方程.
分析:设出直线l的方程,由圆心到直线的距离d与圆的半径及半弦长构成直角三角形求解.注意讨论斜率存在与否.
典例精讲:题型三:弦长问题
解:∵圆C的方程可化为(x-1)2+(y-2)2=52,
∴圆心的坐标为C(1,2),半径r=5.
由圆的性质可知圆的半弦长、半径、弦心距构成直角三角形,
圆心到直线的距离d==3.
当直线AB⊥x轴时,
∵直线l过点P(4,-4),
∴AB的方程为x=4,点C(1,2)到l的距离d=|4-1|=3,满足题意.
典例精讲:题型三:弦长问题
当AB与x轴不垂直时,设方程为y+4=k(x-4)(k≠0),即kx-y-4k-4=0.∵d==3,解得k=-.
∴l的方程为y+4=-(x-4),
即3x+4y+4=0.
综上,直线l的方程为x=4或3x+4y+4=0.
规律方法
求直线与圆相交时弦长的两种方法:
(1)几何法:如图,直线l与圆C交于A,B两点,设弦心距为d,圆的半径为r,弦长为|AB|,则有()2+d2=r2.即|AB|=2.
规律方法
(2)代数法:如图所示,将直线方程与圆的方程联立,设直线与圆的两交点分别是A(x1,y1),B(x2,y2),则|AB|=
=|x1-x2|=·|y1-y2|,其中k为直线l的斜率.
l
A(x1,y1)
B(x2,y2)
课堂练习
1.直线x-y-4=0与圆x2+y2-2x-2y-2=0的位置关系是( )
A.相交但直线不过圆心
B.相切
C.相交且直线过圆心
D.相离
D
课堂练习
2.求斜率为-且与圆x2+y2=16相切的直线方程.
解:设切线方程为y=-x+b,
即2x+3y-3b=0.已知圆的圆心为(0,0),半径r=4,则圆心到切线的距离d==4.解得b=±.故所求切线方程为2x+3y+4=0或2x+3y-4=0.
课堂练习
3.直线x+y-2=0截圆x2+y2=4得到的弦长为( )
B
解析:圆心到直线的距离d==1,
又r=2,所以弦长为2=2.
答案:B
A.1 B.2 C.2 D.2
归纳小结
1.判断直线与圆位置关系的途径主要有两个:一是圆心到直线的距离与圆的半径进行大小比较;二是直线与圆的方程组成的方程组解的个数.两者相比较,前者较形象、直观,便于运算.
2.与圆有关的弦长、切线问题常利用几何法求解,但注意验证所求直线的斜率不存在的情形,避免漏解.
