北师大版高中数学必修一第一章第一节集合的含义课件 (共15张PPT)
文档属性
| 名称 | 北师大版高中数学必修一第一章第一节集合的含义课件 (共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-22 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
高中数学必修1·精品课件
第一章 集合
§1 集合的含义与表示
第1课时 集合的含义
学习目标
1.通过实例理解集合的有关概念.
2.初步理解集合中元素的三个特性.
3.体会元素与集合的属于关系.
4.了解常用数集及其专用符号,学会用集合语言表示有关数学对象.
预习清单 集合与元素的概念
1.集合与元素的定义
2.集合与元素的字母表示
一般地,我们把研究对象统称为 ,把一些元素组成的总体叫做 (简称集).
通常用 表示集合,
用 表示集合中的元素.
元素
集合
大写拉丁字母A,B,C,…
小写拉丁字母a,b,c,…
预习清单 集合与元素的概念
3.元素与集合的关系
(1)属于:如果a是集合A的元素,就说a属于集合A,记作 .
(2)不属于:如果a不是集合A的元素,就说a不属于集合A,记作 .
a∈A
a?A
预习清单 集合与元素的概念
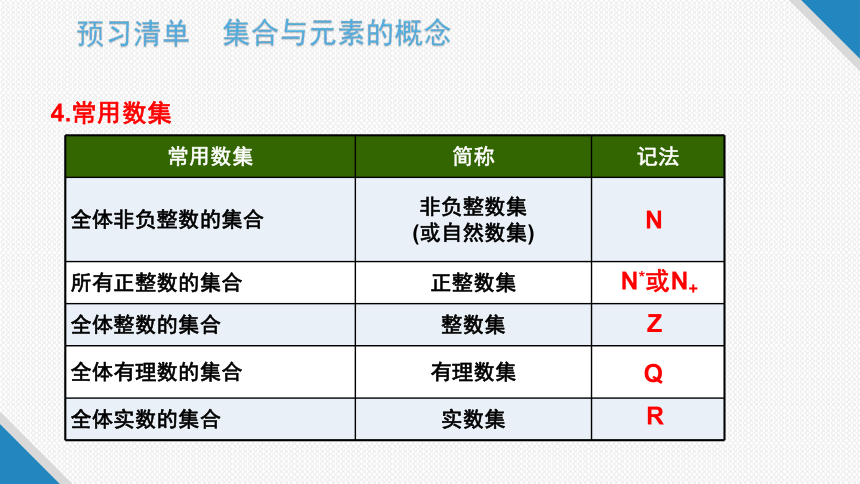
4.常用数集
常用数集 简称 记法
全体非负整数的集合 非负整数集
(或自然数集)
所有正整数的集合 正整数集
全体整数的集合 整数集
全体有理数的集合 有理数集
全体实数的集合 实数集
N
N*或N+
Z
Q
R
合作探究
探究点1 集合定义
问题1:试列举一个集合的例子,并指出集合中的元素.
提示:①“本班全体同学”构成一个集合,每一个同学都是集合中的元素;
②“直线AB上所有点”构成一个集合,集合中的元素是:直线AB上每一个点.
③“方程2x+1=0”的实数解构成一个集合,集合中的元素是实数.
④“不等式3x1<0”的实数解构成一个集合,集合中的元素是满足不等式3x1<0的全体实数.
合作探究
探究点2 集合中元素的特征
【问题2】任意一组对象是否都能组成一个集合?集合中的元素有什么特征?请思考下列问题:
1. 某单位所有的“帅哥”能否构成一个集合?
2. 在一个给定的集合中能否有相同的元素?
3. 本班的全体同学组成一个集合,调整座位后这个集合有没有变化?
不能
不能
没有
合作探究
探究点2 集合中元素的特征
⑴确定性: 集合中的元素必须是确定的.
【结论】:集合元素的特征(性质)
【集合相等】:只要构成两个集合的元素完全一样,就称这两个集合是相等的.
⑶无序性: 集合中的元素是无先后顺序的.
⑵互异性: 集合的元素必须是互不相同的.
典例精讲:题型一:集合的概念
例1:(1)下列对象能组成集合的是( )
A.中央电视台著名节目主持人
B.我市跑得快的汽车
C.上海市所有的中学生
D.香港的高楼
C
(2)以方程x25x60和方程x2x20的解为元素的集合共有 个元素.?
x2,3
x25x60
x2x20
x2,1
3
“著名”无明确标准
“快”的标准不确定
“高”的标准不确定
重复元素只可算1个
典例精讲:题型二:元素与集合的关系问题
下列所给关系正确的是 .
①∈Q ;?②0∈N*;③π?R;④|4|∈Z.
例2:
④
拓展提升:题型二:元素与集合的关系问题
已知集合A含有两个元素a3和2a1,若3∈A,试求实数a的值.
例3:
综上所述,a=0或a=1.
解:
∵3∈A,∴3=a3或3=2a1
(1)若3=a3,
则a=0,
此时集合A中含有两个元素3、1,符合题意;
(2)若3=2a1,
则a=1,
此时集合A中含有两个元素4,3,符合题意.
分类讨论思想
课堂练习
1.下列指定的对象,能构成一个集合的是( )
①很小的数
②不超过 30的非负实数
③直角坐标平面的横坐标与纵坐标相等的点
④?的近似值
⑤高一年级优秀的学生
⑥所有无理数
⑦大于2的整数
⑧正三角形全体
B
A. ②③④⑥⑦⑧ B. ②③⑥⑦⑧
C. ②③⑥⑦ D. ②③⑤⑥⑦⑧
课堂练习
2.判断正误:
(1){(1,2)}={(2,1)}
(2){(1,2),(2,1)}={(2,1),(1,2)}
课堂练习
3.若x∈R,则{3,x,x22x}中的元素x应满足的条件是 .
解析:由元素的互异性可知:
,且,且.
,且,且.
归纳小结
1. 集合的概念
2. 集合中元素的性质
3. 元素与集合的关系
4. 常用的数集
知识点
思想方法:
分类讨论思想
互异性
无序性
确定性
a∈A
a?A
(N,Z,Q,R)
高中数学必修1·精品课件
第一章 集合
§1 集合的含义与表示
第1课时 集合的含义
学习目标
1.通过实例理解集合的有关概念.
2.初步理解集合中元素的三个特性.
3.体会元素与集合的属于关系.
4.了解常用数集及其专用符号,学会用集合语言表示有关数学对象.
预习清单 集合与元素的概念
1.集合与元素的定义
2.集合与元素的字母表示
一般地,我们把研究对象统称为 ,把一些元素组成的总体叫做 (简称集).
通常用 表示集合,
用 表示集合中的元素.
元素
集合
大写拉丁字母A,B,C,…
小写拉丁字母a,b,c,…
预习清单 集合与元素的概念
3.元素与集合的关系
(1)属于:如果a是集合A的元素,就说a属于集合A,记作 .
(2)不属于:如果a不是集合A的元素,就说a不属于集合A,记作 .
a∈A
a?A
预习清单 集合与元素的概念
4.常用数集
常用数集 简称 记法
全体非负整数的集合 非负整数集
(或自然数集)
所有正整数的集合 正整数集
全体整数的集合 整数集
全体有理数的集合 有理数集
全体实数的集合 实数集
N
N*或N+
Z
Q
R
合作探究
探究点1 集合定义
问题1:试列举一个集合的例子,并指出集合中的元素.
提示:①“本班全体同学”构成一个集合,每一个同学都是集合中的元素;
②“直线AB上所有点”构成一个集合,集合中的元素是:直线AB上每一个点.
③“方程2x+1=0”的实数解构成一个集合,集合中的元素是实数.
④“不等式3x1<0”的实数解构成一个集合,集合中的元素是满足不等式3x1<0的全体实数.
合作探究
探究点2 集合中元素的特征
【问题2】任意一组对象是否都能组成一个集合?集合中的元素有什么特征?请思考下列问题:
1. 某单位所有的“帅哥”能否构成一个集合?
2. 在一个给定的集合中能否有相同的元素?
3. 本班的全体同学组成一个集合,调整座位后这个集合有没有变化?
不能
不能
没有
合作探究
探究点2 集合中元素的特征
⑴确定性: 集合中的元素必须是确定的.
【结论】:集合元素的特征(性质)
【集合相等】:只要构成两个集合的元素完全一样,就称这两个集合是相等的.
⑶无序性: 集合中的元素是无先后顺序的.
⑵互异性: 集合的元素必须是互不相同的.
典例精讲:题型一:集合的概念
例1:(1)下列对象能组成集合的是( )
A.中央电视台著名节目主持人
B.我市跑得快的汽车
C.上海市所有的中学生
D.香港的高楼
C
(2)以方程x25x60和方程x2x20的解为元素的集合共有 个元素.?
x2,3
x25x60
x2x20
x2,1
3
“著名”无明确标准
“快”的标准不确定
“高”的标准不确定
重复元素只可算1个
典例精讲:题型二:元素与集合的关系问题
下列所给关系正确的是 .
①∈Q ;?②0∈N*;③π?R;④|4|∈Z.
例2:
④
拓展提升:题型二:元素与集合的关系问题
已知集合A含有两个元素a3和2a1,若3∈A,试求实数a的值.
例3:
综上所述,a=0或a=1.
解:
∵3∈A,∴3=a3或3=2a1
(1)若3=a3,
则a=0,
此时集合A中含有两个元素3、1,符合题意;
(2)若3=2a1,
则a=1,
此时集合A中含有两个元素4,3,符合题意.
分类讨论思想
课堂练习
1.下列指定的对象,能构成一个集合的是( )
①很小的数
②不超过 30的非负实数
③直角坐标平面的横坐标与纵坐标相等的点
④?的近似值
⑤高一年级优秀的学生
⑥所有无理数
⑦大于2的整数
⑧正三角形全体
B
A. ②③④⑥⑦⑧ B. ②③⑥⑦⑧
C. ②③⑥⑦ D. ②③⑤⑥⑦⑧
课堂练习
2.判断正误:
(1){(1,2)}={(2,1)}
(2){(1,2),(2,1)}={(2,1),(1,2)}
课堂练习
3.若x∈R,则{3,x,x22x}中的元素x应满足的条件是 .
解析:由元素的互异性可知:
,且,且.
,且,且.
归纳小结
1. 集合的概念
2. 集合中元素的性质
3. 元素与集合的关系
4. 常用的数集
知识点
思想方法:
分类讨论思想
互异性
无序性
确定性
a∈A
a?A
(N,Z,Q,R)
