高中数学必修一课件:1.1.3.1 并集、交集(共15张PPT)
文档属性
| 名称 | 高中数学必修一课件:1.1.3.1 并集、交集(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-22 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
*
1.1.3 集合的基本运算
第1课时 并集、交集
*
1.理解并集与交集的概念,掌握并集与交集的区别与联系;
2.会求两个已知集合的并集和交集,并能正确应用它们解决一些简单问题.
*
观察集合A,B,C元素间的关系:
A={4,5,6,8},
B={3,5,7,8},
C={3,4,5,6,7,8}
集合C是由属于集合A和集合B的元素构成的.
一、自学(时间约9分钟)
*
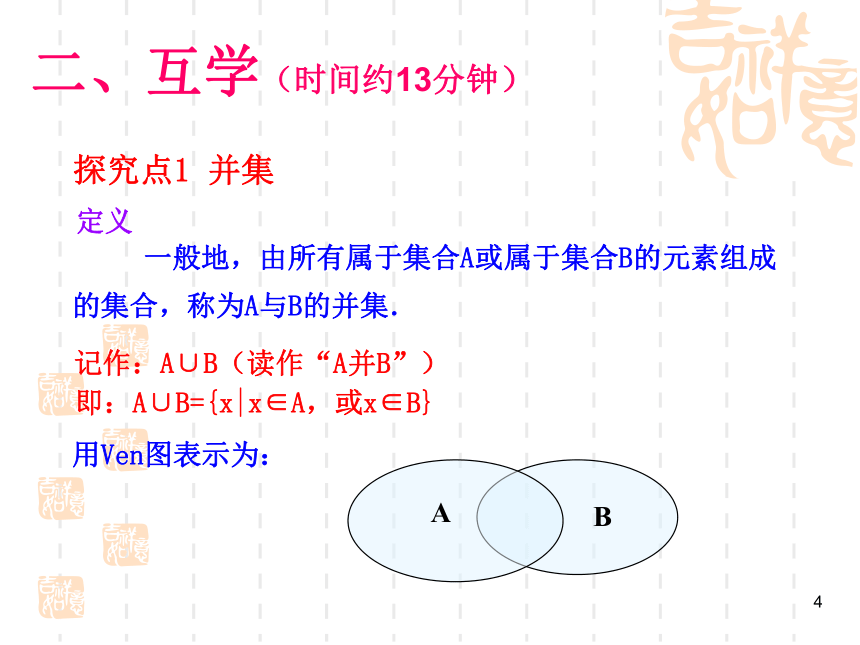
一般地,由所有属于集合A或属于集合B的元素组成的集合,称为A与B的并集.
记作:A∪B(读作“A并B”)
即:A∪B={x|x∈A,或x∈B}
定义
用Ven图表示为:
探究点1 并集
二、互学(时间约13分钟)
*
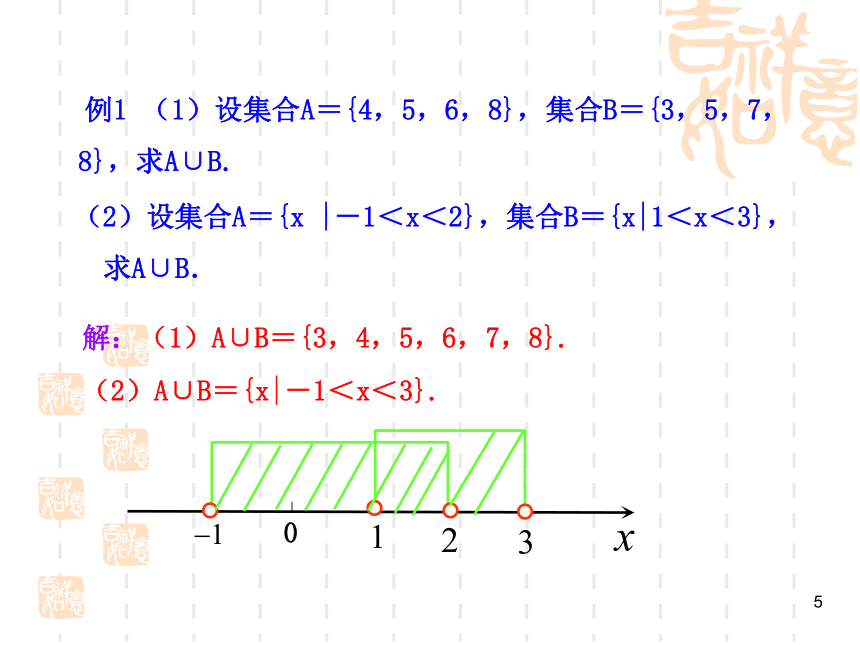
例1 (1)设集合A={4,5,6,8},集合B={3,5,7,8},求A∪B.
解:(1)A∪B={3,4,5,6,7,8}.
(2)设集合A={x |-1<x<2},集合B={x|1<x<3},
求A∪B.
(2)A∪B={x|-1<x<3}.
*
(1)A={3,5,6,8},B={4,5,7,8},求A B;
(2) ,求
解:(1) ={3,4,5,6,7,8}.
(2)
*
观察集合A,B,C元素间的关系:
A={4,3,5};B={2,4,6};C={4}.
集合C的元素既属于A,又属于B,则称C为A与B的交集.
探究点2 交集
*
定义
由属于集合A且属于集合B的所有元素组成的集合,称为A与B的交集,记作A∩B,(读作“A交B”)即
A∩B={x|x∈A且x∈B }.
用Venn图表示为:
*
例2 ⑴ A={2,4,6,8,10},B={3,5,8,12},
C={6,8},求①A∩B; ②A∩(B∩C).
解:①
②
*
(2)设集合A={x |1<x<5},集合B ={x|2<x<6},
求A B.
(1)设集合A={4,5,6,8},集合B={3,5,7,
8,9},求A B.
*
探究点3 并集和交集的性质
(1)A∪A = A∪φ = A∪B B∪A
(2)A∩A = A∩φ = A∩B B∩A
A
A
A
=
=
φ
(3)A A∪B B A∪B
(4)A∩B A A∩B B
(5)A∩B A∪B
三、导学(时间约18分钟)
*
例3 已知A={x|x≤4}, B={x|x>a},若A∪B=R,求实数a的取值范围.
如上图 a≤4.
x
*
1.设A={x|0解:A={x|0A∩B={x|-1A∪B={x|-1四、检学(时间约5分钟)
*
2.已知A={x|-1a},若A∩B=Ф,则实数a的取值范围为______.
3.写出满足条件 的所有集合M.
{3},{1,3},{2,3},{1,2,3}
*
回顾本节课你有什么收获?
⑴ 并集、交集
A∪B={x|x∈A或x∈B},
A∩B={x|x∈A且x∈B};
(2)利用数轴和Venn图求交集,并集;
(3)性质A∩A=A,A∪A=A,
A∩?=?,A∪?=A;
A∩B=B∩A,A∪B=B∪A.
*
1.1.3 集合的基本运算
第1课时 并集、交集
*
1.理解并集与交集的概念,掌握并集与交集的区别与联系;
2.会求两个已知集合的并集和交集,并能正确应用它们解决一些简单问题.
*
观察集合A,B,C元素间的关系:
A={4,5,6,8},
B={3,5,7,8},
C={3,4,5,6,7,8}
集合C是由属于集合A和集合B的元素构成的.
一、自学(时间约9分钟)
*
一般地,由所有属于集合A或属于集合B的元素组成的集合,称为A与B的并集.
记作:A∪B(读作“A并B”)
即:A∪B={x|x∈A,或x∈B}
定义
用Ven图表示为:
探究点1 并集
二、互学(时间约13分钟)
*
例1 (1)设集合A={4,5,6,8},集合B={3,5,7,8},求A∪B.
解:(1)A∪B={3,4,5,6,7,8}.
(2)设集合A={x |-1<x<2},集合B={x|1<x<3},
求A∪B.
(2)A∪B={x|-1<x<3}.
*
(1)A={3,5,6,8},B={4,5,7,8},求A B;
(2) ,求
解:(1) ={3,4,5,6,7,8}.
(2)
*
观察集合A,B,C元素间的关系:
A={4,3,5};B={2,4,6};C={4}.
集合C的元素既属于A,又属于B,则称C为A与B的交集.
探究点2 交集
*
定义
由属于集合A且属于集合B的所有元素组成的集合,称为A与B的交集,记作A∩B,(读作“A交B”)即
A∩B={x|x∈A且x∈B }.
用Venn图表示为:
*
例2 ⑴ A={2,4,6,8,10},B={3,5,8,12},
C={6,8},求①A∩B; ②A∩(B∩C).
解:①
②
*
(2)设集合A={x |1<x<5},集合B ={x|2<x<6},
求A B.
(1)设集合A={4,5,6,8},集合B={3,5,7,
8,9},求A B.
*
探究点3 并集和交集的性质
(1)A∪A = A∪φ = A∪B B∪A
(2)A∩A = A∩φ = A∩B B∩A
A
A
A
=
=
φ
(3)A A∪B B A∪B
(4)A∩B A A∩B B
(5)A∩B A∪B
三、导学(时间约18分钟)
*
例3 已知A={x|x≤4}, B={x|x>a},若A∪B=R,求实数a的取值范围.
如上图 a≤4.
x
*
1.设A={x|0
*
2.已知A={x|-1
3.写出满足条件 的所有集合M.
{3},{1,3},{2,3},{1,2,3}
*
回顾本节课你有什么收获?
⑴ 并集、交集
A∪B={x|x∈A或x∈B},
A∩B={x|x∈A且x∈B};
(2)利用数轴和Venn图求交集,并集;
(3)性质A∩A=A,A∪A=A,
A∩?=?,A∪?=A;
A∩B=B∩A,A∪B=B∪A.
