高中数学必修一课件:2.1.2.1 指数函数的图象及性质(共15张PPT)
文档属性
| 名称 | 高中数学必修一课件:2.1.2.1 指数函数的图象及性质(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-22 16:24:54 | ||
图片预览






文档简介
(共15张PPT)
2.1.2 指数函数及其性质
第1课时 指数函数的图象及性质
1.记住指数函数的概念及表达式.
2.会用描点法画出简单指数函数的图象,并会描述指数函数的图象特征.
3.会根据指数函数图象的特征找出指数函数的性质.
4.会根据条件求指数函数的解析式.
5.会应用指数函数的性质解决有关问题.
某种细胞分裂时,由1个分裂成2个,2个分裂成4个……,这样一个细胞分裂x次,得到的细胞的个数y与x的函数关系式是:y=2x
在这个函数里,自变量x出现在指数的位置上,而底数2是一个大于零且不等于1的常数.
一、自学(时间约9分钟)
再来看一个问题:《庄子·逍遥游》记载:一尺之椎,日取其半,万世不竭.意思是一尺长的木棒,一天截取一半,很长时间也截取不完.这样的一个木棒截取x次,剩余长度y与x的关系是:
在这个函数里,自变量x出现在指数的位置上,而底数是一个大于零且不等于1的常数.
形如y=2x, 的函数是指数函数.那么,指数函数是怎样定义的呢?
一般地,函数y=ax(a>0且a≠1),叫做指数函数.
其中x是自变量,函数的定义域是R
探究点1 指数函数的概念
二、互学(时间约13分钟)
例6 已知指数函数 f(x)=ax(a>0,a≠1) 的图象经过点(3,π),求f(0)、f(1)、f(-3)的值.
解:指数函数的图象经过点(3,π),有f(3)=π,
即 a3=π 解得
于是
思考:确定一个指数函数需要什么条件?
想一想
所以
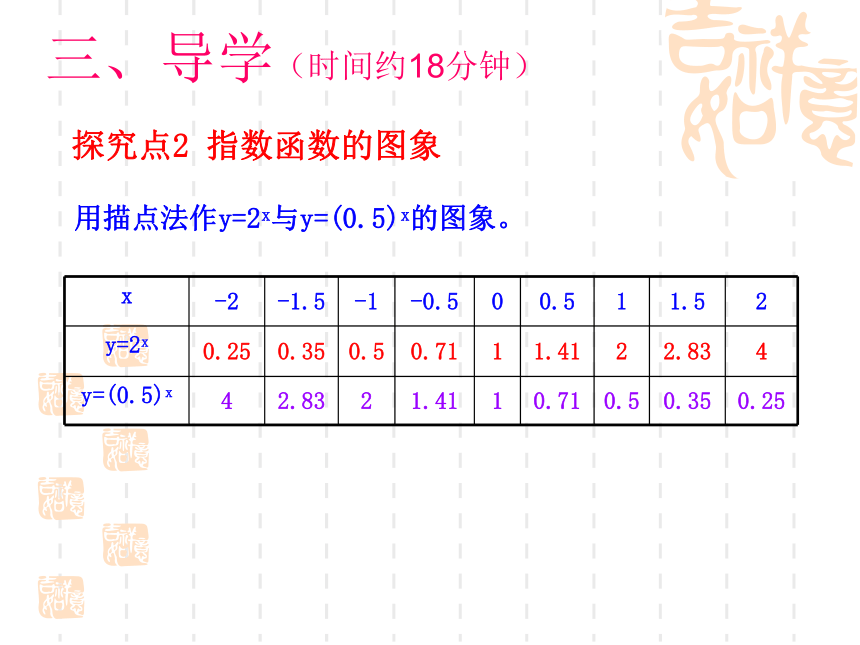
探究点2 指数函数的图象
用描点法作y=2x与y=(0.5)x的图象。
三、导学(时间约18分钟)
x -2 -1.5 -1 -0.5 0 0.5 1 1.5 2
y=2x 0.25 0.35 0.5 0.71 1 1.41 2 2.83 4
y=(0.5)x 4 2.83 2 1.41 1 0.71 0.5 0.35 0.25
我们再看部分函数的图象
探究点3 指数函数的性质
底数
图象
定义域 R
值域
性质 (1)过定点(0,1),x=0时,y=1
(2)R上减函数 (2)R上增函数
例7.比较下列各题中两个值的大小
分析:根据指数函数的性质进行比较。
解:(1)根据函数y=1.7x的性质,1.72.5<1.73。
(2)根据函数y=0.8x的性质,0.8-0.1<0.8-0.2。
(3)根据函数y=1.7x的性质,1.70.3>1.70=1,
根据函数y=0.9x的性质,0.93.1<0.90=1,
所以1.70.3>0.93.1
1.在同一平面直角坐标系中,画出下列函数的图象:
四、检学(时间约5分钟)
2.求下列函数的定义域:
答案:
一般地,函数y=ax(a>0且a≠1),叫做指数函数.
1.指数函数的定义
2.指数函数的图象与性质
2.1.2 指数函数及其性质
第1课时 指数函数的图象及性质
1.记住指数函数的概念及表达式.
2.会用描点法画出简单指数函数的图象,并会描述指数函数的图象特征.
3.会根据指数函数图象的特征找出指数函数的性质.
4.会根据条件求指数函数的解析式.
5.会应用指数函数的性质解决有关问题.
某种细胞分裂时,由1个分裂成2个,2个分裂成4个……,这样一个细胞分裂x次,得到的细胞的个数y与x的函数关系式是:y=2x
在这个函数里,自变量x出现在指数的位置上,而底数2是一个大于零且不等于1的常数.
一、自学(时间约9分钟)
再来看一个问题:《庄子·逍遥游》记载:一尺之椎,日取其半,万世不竭.意思是一尺长的木棒,一天截取一半,很长时间也截取不完.这样的一个木棒截取x次,剩余长度y与x的关系是:
在这个函数里,自变量x出现在指数的位置上,而底数是一个大于零且不等于1的常数.
形如y=2x, 的函数是指数函数.那么,指数函数是怎样定义的呢?
一般地,函数y=ax(a>0且a≠1),叫做指数函数.
其中x是自变量,函数的定义域是R
探究点1 指数函数的概念
二、互学(时间约13分钟)
例6 已知指数函数 f(x)=ax(a>0,a≠1) 的图象经过点(3,π),求f(0)、f(1)、f(-3)的值.
解:指数函数的图象经过点(3,π),有f(3)=π,
即 a3=π 解得
于是
思考:确定一个指数函数需要什么条件?
想一想
所以
探究点2 指数函数的图象
用描点法作y=2x与y=(0.5)x的图象。
三、导学(时间约18分钟)
x -2 -1.5 -1 -0.5 0 0.5 1 1.5 2
y=2x 0.25 0.35 0.5 0.71 1 1.41 2 2.83 4
y=(0.5)x 4 2.83 2 1.41 1 0.71 0.5 0.35 0.25
我们再看部分函数的图象
探究点3 指数函数的性质
底数
图象
定义域 R
值域
性质 (1)过定点(0,1),x=0时,y=1
(2)R上减函数 (2)R上增函数
例7.比较下列各题中两个值的大小
分析:根据指数函数的性质进行比较。
解:(1)根据函数y=1.7x的性质,1.72.5<1.73。
(2)根据函数y=0.8x的性质,0.8-0.1<0.8-0.2。
(3)根据函数y=1.7x的性质,1.70.3>1.70=1,
根据函数y=0.9x的性质,0.93.1<0.90=1,
所以1.70.3>0.93.1
1.在同一平面直角坐标系中,画出下列函数的图象:
四、检学(时间约5分钟)
2.求下列函数的定义域:
答案:
一般地,函数y=ax(a>0且a≠1),叫做指数函数.
1.指数函数的定义
2.指数函数的图象与性质
