高中数学必修一课件:2.1.2.2 指数函数及其性质的应用(共22张PPT)
文档属性
| 名称 | 高中数学必修一课件:2.1.2.2 指数函数及其性质的应用(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-22 16:28:05 | ||
图片预览








文档简介
(共22张PPT)
*
第2课时 指数函数及其性质的应用
*
1.复习回顾指数函数的概念、图象和性质;
2.通过典型例题初步掌握指数函数在解决实际问题中的应用;
3.通过典型例题初步掌握指数函数的图象和性质在解题中的应用
*
一般地,函数y=ax(a>0且a≠1),叫做指数函数.
1.指数函数的定义
一、自学(时间约9分钟)
*
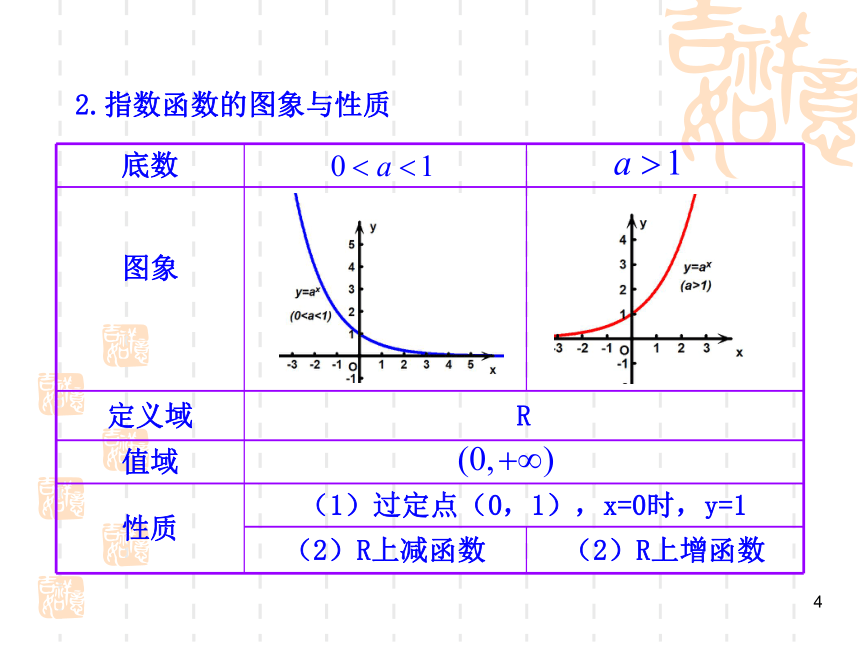
2.指数函数的图象与性质
底数
图象
定义域 R
值域
性质 (1)过定点(0,1),x=0时,y=1
(2)R上减函数 (2)R上增函数
*
探究点1 指数函数在实际问题中的应用
例8.截止到1999年底,我国人口约13亿。如果今后能将人口年平均增长率控制在1%,那么经过20年后,我国人口数最多为多少?(精确到亿)
分析:可以从经过1年后、2年后、3年后等具体的人口数入手,归纳经过x年后的人口数的函数关系式,再把经过20年后的人口数表示出来,进行具体的计算。
二、互学(时间约13分钟)
*
解:设今后人口的年平均增长率是1%,经过x年后,我国的人口数为y亿.
经过1年即2000年,人口数为
经过2年即2001年,人口数为
(亿);
(亿).
*
经过3年即2002年,人口数为
……
所以,经过x年,人口数为
当x=20时, (亿)。
所以,经过20年后,我国的人口数最多为16亿。
(亿);
*
【点评】在实际问题中,经常会遇到类似例8的指数增长
模型:设原有量为N,每次的增长率为p,经过x次增长,该量增长到y,则 形如
的函数是一种指数型函数,这是非常有用的函数模型。
*
探究点2 人口增长率问题的进一步探究
(1)如果人口增长率提高一个百分点,利用计算器分别计算20年,33年后我国的人口数。
这时函数模型是
所以,20年后的人口数是
33年后人口数是
以1999年的13亿为基准。
*
(2)如果人口年平均增长率保持在2%,利用计算器分别计算2020到2100年,每隔5年相应的人口数。
以例题中计算的2020年我国的人口数16亿为基准。
这时函数模型是
2025年的人口数是
2030年的人口数是
*
2035年的人口数是
2040年的人口数是
2045年的人口数是
2050年的人口数是
2055年的人口数是
2060年的人口数是
2065年的人口数是
*
2070年的人口数是
2075年的人口数是
2080年的人口数是
2085年的人口数是
2090年的人口数是
2095年的人口数是
2100年的人口数是
*
(3)你看到人口的增长成什么趋势?
我们使用软件画出函数 的图象
从这个图象上可以看出随着x的增大,函数值的增长非常迅速,呈现一种“爆炸式”的增长趋势。
*
(4)你是如何看待我国的计划生育政策的?
计划生育是我国的基本国策,是千年大计!
*
探究点3 指数函数在解题中的应用
例9.将下列各数值按从小到大的顺序排列
分析:根据指数函数的性质,指数幂的运算法则进行,注意采用中间值0和1进行比较。
解:
所以,
三、导学(时间约18分钟)
*
例10.解下列不等式:
分析:根据指数函数的单调性把指数不等式转化为代数不等式。
解:(1)由 ,得
根据指数函数的单调性得
解这个不等式得
*
(2)当0 3x-1≥2x-4
解这个不等式得x≥-3.
当a>1时,根据指数函数的单调性得不等式3x-1≤2x-4
解这个不等式得x≤-3.
所以,当0当a>1时,不等式的解是x≤-3.
*
【点评】本题的不等式通常称为指数不等式,解这类不等式的基本方法是根据指数函数的单调性转化为代数不等式,在底数不确定时要注意分类讨论。
*
1.某工厂现在的年利润是1000万元,该工厂年利润的增长率是20%,则10年后该工厂的年利润是多少万元?(精确到万元)
答案:
四、检学(时间约5分钟)
*
2.比较下列各数的大小:
答案:
3.解方程
解析:
解方程得x=1
答案:
*
1.指数型函数模型是应用十分广泛的一类函数模型,当指数函数的底数大于1时,随着自变量的增加,函数值呈现“爆炸式”增长。
2.根据指数函数性质进行数值的大小比较时,要注意采用中间值0、1进行归类比较。
*
3.解指数不等式或者指数方程时,要注意根据指数函数的单调性进行转化,转化为代数不等式或者代数方程求解,在底数不确定时要注意分类讨论,这里体现了化归转化思想和分类讨论思想。
*
第2课时 指数函数及其性质的应用
*
1.复习回顾指数函数的概念、图象和性质;
2.通过典型例题初步掌握指数函数在解决实际问题中的应用;
3.通过典型例题初步掌握指数函数的图象和性质在解题中的应用
*
一般地,函数y=ax(a>0且a≠1),叫做指数函数.
1.指数函数的定义
一、自学(时间约9分钟)
*
2.指数函数的图象与性质
底数
图象
定义域 R
值域
性质 (1)过定点(0,1),x=0时,y=1
(2)R上减函数 (2)R上增函数
*
探究点1 指数函数在实际问题中的应用
例8.截止到1999年底,我国人口约13亿。如果今后能将人口年平均增长率控制在1%,那么经过20年后,我国人口数最多为多少?(精确到亿)
分析:可以从经过1年后、2年后、3年后等具体的人口数入手,归纳经过x年后的人口数的函数关系式,再把经过20年后的人口数表示出来,进行具体的计算。
二、互学(时间约13分钟)
*
解:设今后人口的年平均增长率是1%,经过x年后,我国的人口数为y亿.
经过1年即2000年,人口数为
经过2年即2001年,人口数为
(亿);
(亿).
*
经过3年即2002年,人口数为
……
所以,经过x年,人口数为
当x=20时, (亿)。
所以,经过20年后,我国的人口数最多为16亿。
(亿);
*
【点评】在实际问题中,经常会遇到类似例8的指数增长
模型:设原有量为N,每次的增长率为p,经过x次增长,该量增长到y,则 形如
的函数是一种指数型函数,这是非常有用的函数模型。
*
探究点2 人口增长率问题的进一步探究
(1)如果人口增长率提高一个百分点,利用计算器分别计算20年,33年后我国的人口数。
这时函数模型是
所以,20年后的人口数是
33年后人口数是
以1999年的13亿为基准。
*
(2)如果人口年平均增长率保持在2%,利用计算器分别计算2020到2100年,每隔5年相应的人口数。
以例题中计算的2020年我国的人口数16亿为基准。
这时函数模型是
2025年的人口数是
2030年的人口数是
*
2035年的人口数是
2040年的人口数是
2045年的人口数是
2050年的人口数是
2055年的人口数是
2060年的人口数是
2065年的人口数是
*
2070年的人口数是
2075年的人口数是
2080年的人口数是
2085年的人口数是
2090年的人口数是
2095年的人口数是
2100年的人口数是
*
(3)你看到人口的增长成什么趋势?
我们使用软件画出函数 的图象
从这个图象上可以看出随着x的增大,函数值的增长非常迅速,呈现一种“爆炸式”的增长趋势。
*
(4)你是如何看待我国的计划生育政策的?
计划生育是我国的基本国策,是千年大计!
*
探究点3 指数函数在解题中的应用
例9.将下列各数值按从小到大的顺序排列
分析:根据指数函数的性质,指数幂的运算法则进行,注意采用中间值0和1进行比较。
解:
所以,
三、导学(时间约18分钟)
*
例10.解下列不等式:
分析:根据指数函数的单调性把指数不等式转化为代数不等式。
解:(1)由 ,得
根据指数函数的单调性得
解这个不等式得
*
(2)当0
解这个不等式得x≥-3.
当a>1时,根据指数函数的单调性得不等式3x-1≤2x-4
解这个不等式得x≤-3.
所以,当0
*
【点评】本题的不等式通常称为指数不等式,解这类不等式的基本方法是根据指数函数的单调性转化为代数不等式,在底数不确定时要注意分类讨论。
*
1.某工厂现在的年利润是1000万元,该工厂年利润的增长率是20%,则10年后该工厂的年利润是多少万元?(精确到万元)
答案:
四、检学(时间约5分钟)
*
2.比较下列各数的大小:
答案:
3.解方程
解析:
解方程得x=1
答案:
*
1.指数型函数模型是应用十分广泛的一类函数模型,当指数函数的底数大于1时,随着自变量的增加,函数值呈现“爆炸式”增长。
2.根据指数函数性质进行数值的大小比较时,要注意采用中间值0、1进行归类比较。
*
3.解指数不等式或者指数方程时,要注意根据指数函数的单调性进行转化,转化为代数不等式或者代数方程求解,在底数不确定时要注意分类讨论,这里体现了化归转化思想和分类讨论思想。
