高中数学必修一课件:2.2.2.1 对数函数的图象及性质(共24张PPT)
文档属性
| 名称 | 高中数学必修一课件:2.2.2.1 对数函数的图象及性质(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-22 16:27:40 | ||
图片预览





文档简介
(共24张PPT)
2.2.2 对数函数及其性质
第1课时 对数函数的图象及性质
(1)理解对数函数的概念;
(2)掌握对数函数的图象和性质;
(3)进一步加强数形结合意识。
人们经过长期实践,获得了生物体内碳14含量P与死亡年数t之间的关系:
由指数与对数的关系,此指数式写成对数式是:
根据问题的实际意义可知,对于每一个碳14含量
P,通过对应关系 ,都有一个确定的年代t与它对应,所以,t是P的函数.
一、自学(时间约9分钟)
思考:湖南长沙马王堆汉墓女尸出土时碳14的残余量约占原始含量的76.7%.你能推算马王堆古墓的年代吗?
考古学家一般通过提取附着在出土文物、古遗址上死亡生物体的残留物,利用(*)式估算出土文物或古遗址的年代.
答案:t≈2193
一般地,把函数 叫做对数函数,其中x是自变量,函数的定义域是 .
1.对数函数的定义
二、互学(时间约13分钟)
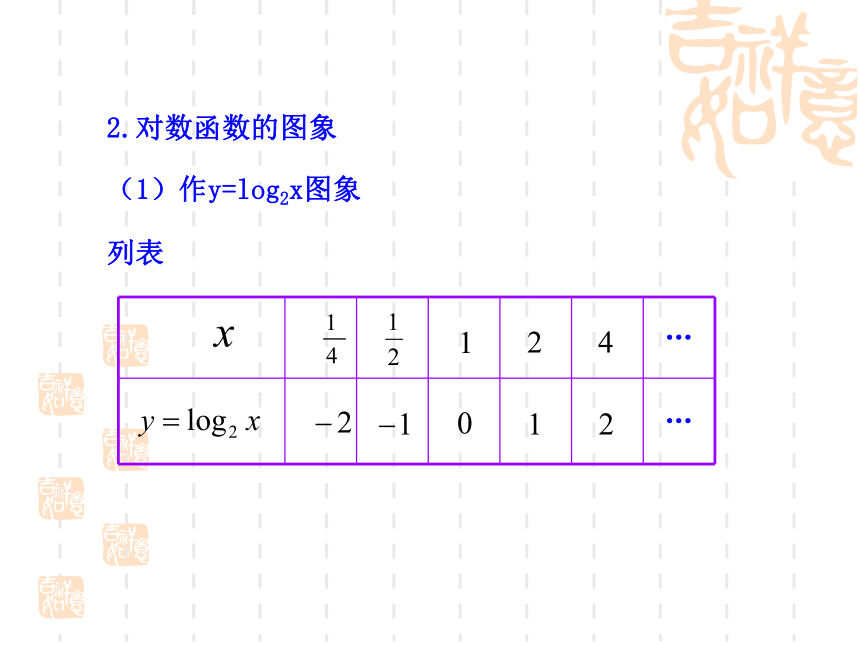
2.对数函数的图象
(1)作y=log2x图象
列表
…
…
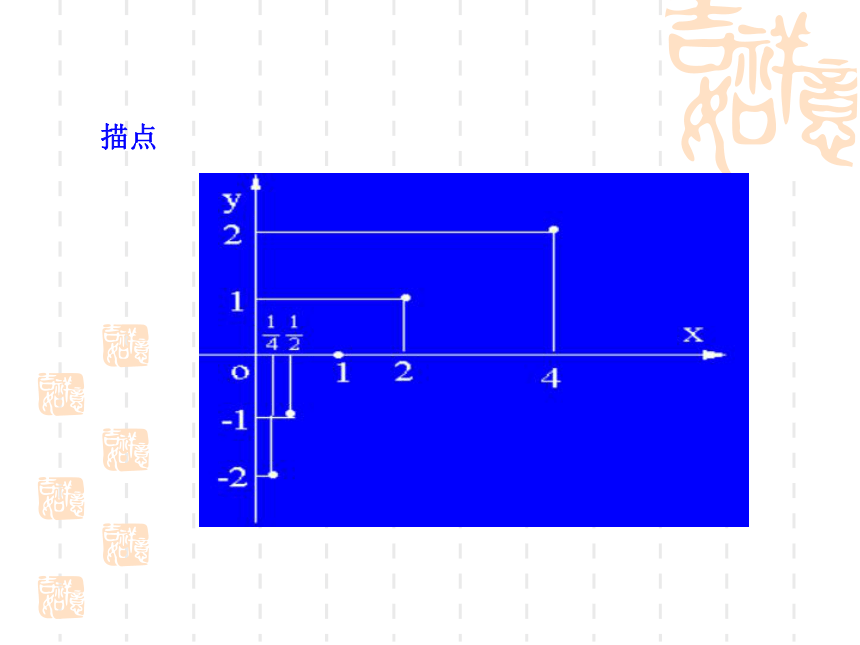
描点
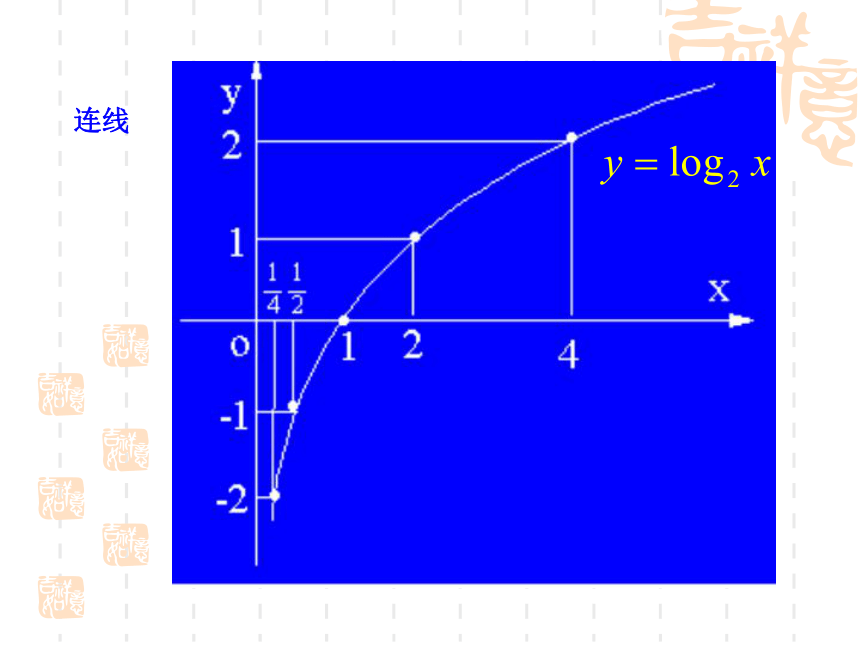
连线
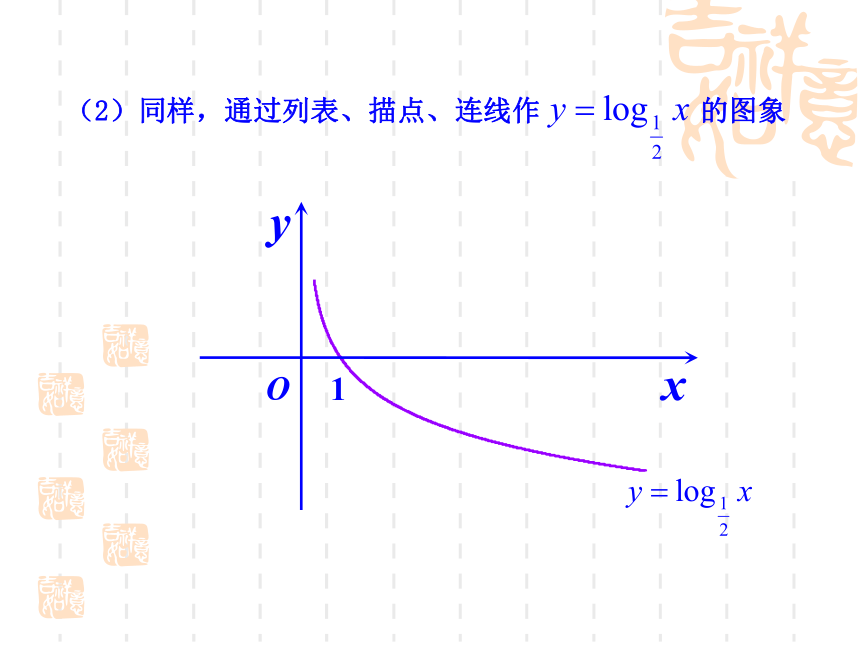
(2)同样,通过列表、描点、连线作 的图象
O
y
x
1
注意:利用换底公式,可以得到:
又点(x,y)和点(x,-y)关于x轴对称,所以y=log2x和
的图象关于x轴对称.
因此我们还可以利用对称得到 的图象.
y
O
x
1
(1)在同一坐标系中画出下列函数的图象
思考
0 1
1
(2)你能否猜测 与
分别与下图哪个图象相似.
x
y
图
像
性
质
定义域
值域
例1:求下列函数的定义域:
(1)y=logax2 (2)y=loga(4-x)
(3)y=loga(9-x)
分析:主要利用对数函数y=logax的定义域为
(0,+∞)求解。
三、导学(时间约18分钟)
(1)因为x2 >0,
所以函数y=loga(4-x)的定义域是
所以函数y=loga(9-x)的定义域是
所以函数y=logax2的定义域是
(2)因为4-x>0,
(3)因为9-x>0,
{x│x<9}
即x<9,
{x│x<4}
即x<4,
{x│x≠0}
即x≠0,
练习1:求下列函数的定义域:
解:(1)因为1-x>0,即x<1所以函数y=log5(1-x)的定义域为{x|x<1}
(2)因为x>0且
所以函数 的定义域为{x|x>0且x≠1}
即x>0且x≠1
(3)因为 ,即
所以函数 的定义域为
(4)因为x>0且
所以函数 的定义域为
即
小结:由具体函数式求定义域,考虑:
(1)分母不等于0;
(2)偶次方根被开方数非负;
(3)零指数幂底数不为0;
(4)对数式考虑真数大于0;
(5)实际问题要有实际意义。
比较下列各组数中两个值的大小:
(1) log23.4,log28.5
(2) log0.31.8,log0.32.7
(3) loga5.1,loga5.9 ( a>0,且a≠1 )
解:⑴考察对数函数y=log2x,因为它的底数2>1,所以它在(0,+∞)上是增函数,于是log23.4<log28.5
⑵考察对数函数y=log0.3x,因为它的底数0<0.3<1,所以它在(0,+∞)上是减函数,于是log0.31.8>log0.32.7
四、检学(时间约5分钟)
⑶ loga5.1, loga5.9 (a>0,且 a≠1)
分析:对数函数的增减性决定于对数的底数是大于1还是小于1.而已知条件中并未指出底数a与1哪个大,因此需要对底数a进行讨论:
当0<a<1时,因为函数y=logax在(0,+∞)上是减函数,
解:当a>1时,因为函数y=logax在(0,+∞)上是增函数,
于是 loga5.1<loga5.9
于是 loga5.1>loga5.9
2.分类讨论的思想.
点评 1.两个同底数的对数比较大小的一般步骤:
(2)根据对数底数判断对数函数单调性;
(3)比较真数大小,然后利用对数函数的单调性判断两对数值的大小.
(1)确定所要考查的对数函数;
利用对数函数的增减性比较两个对数的大小时,
要分情况对底数进行讨论来比较两个对数的大小.
对底数与1的大小关系未明确指出时,
通过本节的学习,说出你的收获。
对数函数
图 象
性 质
概 念
2.2.2 对数函数及其性质
第1课时 对数函数的图象及性质
(1)理解对数函数的概念;
(2)掌握对数函数的图象和性质;
(3)进一步加强数形结合意识。
人们经过长期实践,获得了生物体内碳14含量P与死亡年数t之间的关系:
由指数与对数的关系,此指数式写成对数式是:
根据问题的实际意义可知,对于每一个碳14含量
P,通过对应关系 ,都有一个确定的年代t与它对应,所以,t是P的函数.
一、自学(时间约9分钟)
思考:湖南长沙马王堆汉墓女尸出土时碳14的残余量约占原始含量的76.7%.你能推算马王堆古墓的年代吗?
考古学家一般通过提取附着在出土文物、古遗址上死亡生物体的残留物,利用(*)式估算出土文物或古遗址的年代.
答案:t≈2193
一般地,把函数 叫做对数函数,其中x是自变量,函数的定义域是 .
1.对数函数的定义
二、互学(时间约13分钟)
2.对数函数的图象
(1)作y=log2x图象
列表
…
…
描点
连线
(2)同样,通过列表、描点、连线作 的图象
O
y
x
1
注意:利用换底公式,可以得到:
又点(x,y)和点(x,-y)关于x轴对称,所以y=log2x和
的图象关于x轴对称.
因此我们还可以利用对称得到 的图象.
y
O
x
1
(1)在同一坐标系中画出下列函数的图象
思考
0 1
1
(2)你能否猜测 与
分别与下图哪个图象相似.
x
y
图
像
性
质
定义域
值域
例1:求下列函数的定义域:
(1)y=logax2 (2)y=loga(4-x)
(3)y=loga(9-x)
分析:主要利用对数函数y=logax的定义域为
(0,+∞)求解。
三、导学(时间约18分钟)
(1)因为x2 >0,
所以函数y=loga(4-x)的定义域是
所以函数y=loga(9-x)的定义域是
所以函数y=logax2的定义域是
(2)因为4-x>0,
(3)因为9-x>0,
{x│x<9}
即x<9,
{x│x<4}
即x<4,
{x│x≠0}
即x≠0,
练习1:求下列函数的定义域:
解:(1)因为1-x>0,即x<1所以函数y=log5(1-x)的定义域为{x|x<1}
(2)因为x>0且
所以函数 的定义域为{x|x>0且x≠1}
即x>0且x≠1
(3)因为 ,即
所以函数 的定义域为
(4)因为x>0且
所以函数 的定义域为
即
小结:由具体函数式求定义域,考虑:
(1)分母不等于0;
(2)偶次方根被开方数非负;
(3)零指数幂底数不为0;
(4)对数式考虑真数大于0;
(5)实际问题要有实际意义。
比较下列各组数中两个值的大小:
(1) log23.4,log28.5
(2) log0.31.8,log0.32.7
(3) loga5.1,loga5.9 ( a>0,且a≠1 )
解:⑴考察对数函数y=log2x,因为它的底数2>1,所以它在(0,+∞)上是增函数,于是log23.4<log28.5
⑵考察对数函数y=log0.3x,因为它的底数0<0.3<1,所以它在(0,+∞)上是减函数,于是log0.31.8>log0.32.7
四、检学(时间约5分钟)
⑶ loga5.1, loga5.9 (a>0,且 a≠1)
分析:对数函数的增减性决定于对数的底数是大于1还是小于1.而已知条件中并未指出底数a与1哪个大,因此需要对底数a进行讨论:
当0<a<1时,因为函数y=logax在(0,+∞)上是减函数,
解:当a>1时,因为函数y=logax在(0,+∞)上是增函数,
于是 loga5.1<loga5.9
于是 loga5.1>loga5.9
2.分类讨论的思想.
点评 1.两个同底数的对数比较大小的一般步骤:
(2)根据对数底数判断对数函数单调性;
(3)比较真数大小,然后利用对数函数的单调性判断两对数值的大小.
(1)确定所要考查的对数函数;
利用对数函数的增减性比较两个对数的大小时,
要分情况对底数进行讨论来比较两个对数的大小.
对底数与1的大小关系未明确指出时,
通过本节的学习,说出你的收获。
对数函数
图 象
性 质
概 念
