高中数学必修一课件:2.2.2.2 对数函数及其性质的应用(共20张PPT)
文档属性
| 名称 | 高中数学必修一课件:2.2.2.2 对数函数及其性质的应用(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-22 16:28:32 | ||
图片预览







文档简介
(共20张PPT)
第2课时 对数函数及其性质的应用
1.进一步掌握对数函数的图象和性质;
2.会利用对数函数的图象和性质解决有关问题;
3.了解底数相同的指数函数和对数函数互为反函数。
20世纪80年代末,教会用高科技手段澄清了一个历史大悬案,这就是关于耶稣裹尸布真伪的鉴定,鉴定证明了那块使人崇敬了多年的裹尸布是假的,它的原料纤维是十三世纪才种出来的,而此时耶稣已被钉在十字架上1200多年了。这个轰动世界的年代鉴定是由研究碳14含量做出的。
一、自学(时间约9分钟)
(1)对数函数的定义:
函数y=logax (a>0且a≠1)叫做对数函数,定义域为(0,+∞),值域为R.
1.温故知新
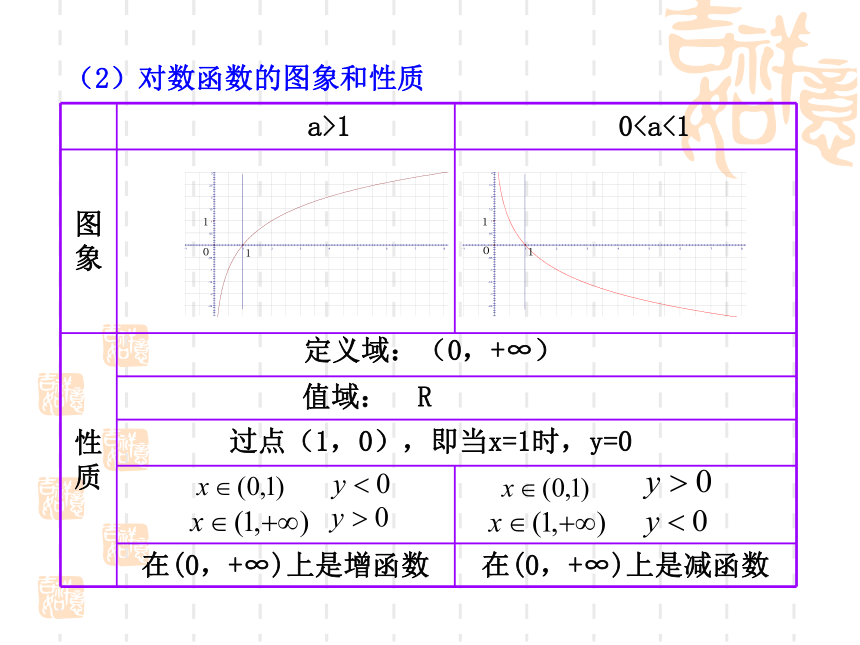
(2)对数函数的图象和性质
过点(1,0),即当x=1时,y=0
值域: R
定义域:(0,+∞)
a>1 0图象
性 质
在(0,+∞)上是增函数 在(0,+∞)上是减函数
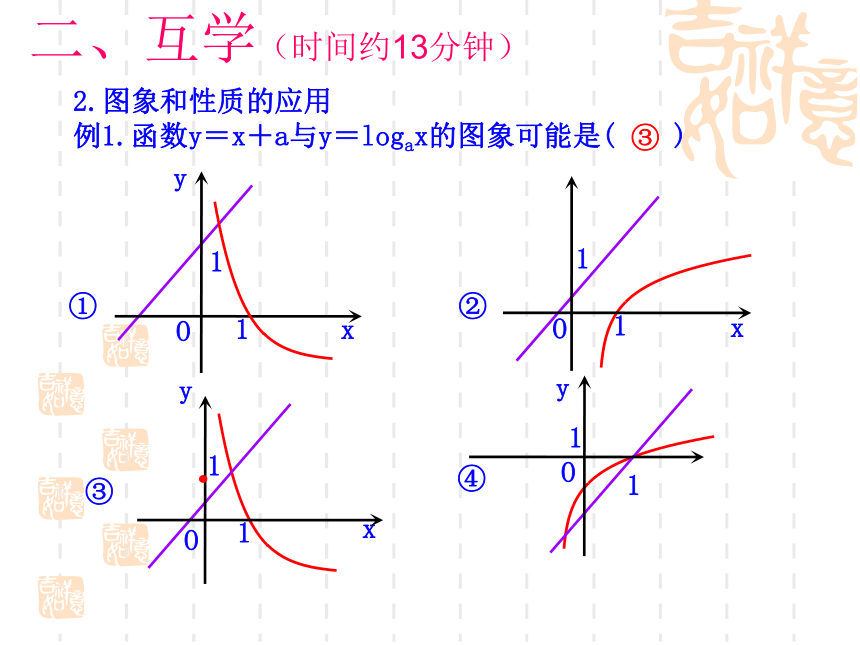
2.图象和性质的应用
例1.函数y=x+a与y=logax的图象可能是( )
①
②
1
1
O
x
y
1
1
O
x
1
1
O
y
④
③
1
1
O
x
y
③
二、互学(时间约13分钟)
例2:比较下列各组数中两个值的大小:
(1)log67与log76
解:(1)∵ log67>log66=1
且log76<log77=1
∴log67 >log76
(2)log3π与log20.8
(2)∵log3π>log31=0
且log20.8<log21=0
∴log3π>log20.8
(3)log27与log37
(4)log0.20.8 与log0.30.8
(3)
(4)
1.同底数比较大小时
(1)当底数确定时,则可由函数的单调性直接进行判断;
(2)当底数不确定时,应对底数进行分类讨论;
3.若底数、真数都不相同, 则常借助1、0等中间量进行比较
2.同真数的比较大小,常借助函数图象或对数的运算性质变形后进行比较
点评:两个对数比较大小
练习 比较大小
函数x=log2y,y是自变量,x是y的函数,定义域为(0,
+∞),值域为R.
函数y=2x,x是自变量,y是x的函数,定义域为R,
值域为 (0, +∞).
3.探究:对数函数与指数函数之间的关系
这时称函数x=log2y是函数y=2x的反函数.
在函数x=log2y中,y是自变量,x是函数.
三、导学(时间约18分钟)
但是习惯上,通常用x表示自变量,y表示函数.
为此,常常对调函数x=log2y中的字母x与y
把它写成函数y=log2x.
这样对数函数y=log2x与指数函数y=2x互为反函数。
推广 对数函数y=logax与指数函数y=ax互为反函数。
1.设0<x<1,a>0且a≠1,试比较
|loga(1-x)|与|loga(1+x)|的大小。
|loga(1-x)|-|loga(1+x)|=loga(1-x)+loga(1+x)
解:∵0<x<1
∴0<1-x<1,1<1+x<2,0<x2<1
即|loga(1-x)|-|loga(1+x)|>0
∴|loga(1-x)|>|loga(1+x)|
当0=loga(1-x)(1+x)=loga(1-x2)>0
∴ 0<(1-x)(1+x)=1-x2<1
四、检学(时间约5分钟)
|loga(1-x)|-|loga(1+x)|
即|loga(1-x)|-|loga(1+x)|>0
∴ |loga(1-x)|>|loga(1+x)|
当a>1时,则有
=-loga(1-x)-loga(1+x) =-loga(1-x)(1+x)
=- loga(1-x2)>0
当a>1时,有
当0|loga(1-x)|>|loga(1+x)|
|loga(1-x)|>|loga(1+x)|.
综上所述,对于0<x<1,a>0 且 a≠1的一切值总有
由以上分类讨论,得
|loga(1-x)|>|loga(1+x)|
2.若函数f(x)=logax (a>0且a≠1)在区间[a, 2a]上的最大值是最小值的3倍,求a的值.
解:当a>1时,f(x)=logax在区间[a,2a]上是增函数,
综上所述, 或
当03.溶液酸碱度的测量.
溶液酸碱度是通过pH刻画的. pH的计算公式为
pH=-lg[H+],其中[H+]表示溶液中氢离子的浓度,单位是摩尔/升.
(1)根据对数函数性质及上述pH的计算公式,说明溶液酸碱度与溶液中氢离子的浓度之间的变化关系;
(2)已知纯净水中氢离子的浓度为[H+]=10-7摩尔/升,计算纯净水的pH.
lg[H+]增大,从而-lg[H+]减小,
解:(1)根据对数函数的性质,在(0,+∞)上,随着[H+]的增大,
所以,溶液中氢离子的浓度越大,PH就越小,即溶液的酸性越强。
(2)当[H+] =10-7摩尔/升时,PH=-lg10-7=7,所以,纯净水的PH是7.
于是由PH=-lg[H+]知,PH随着[H+]增大而减小,
1.掌握利用对数函数的性质比较数的大小的方法;
2.对数函数单调性的灵活应用;
3.对数函数与指数函数互为反函数.
作 业
1.将log0.73,log87,0.9-3.1
由小到大排列.
2.已知3lg(x-3)<1, 求x的取值范围.
4.设a>0,且a≠1,比较loga(a2+1)与loga(a3+1)的大小.
3.求下列函数的定义域、值域
第2课时 对数函数及其性质的应用
1.进一步掌握对数函数的图象和性质;
2.会利用对数函数的图象和性质解决有关问题;
3.了解底数相同的指数函数和对数函数互为反函数。
20世纪80年代末,教会用高科技手段澄清了一个历史大悬案,这就是关于耶稣裹尸布真伪的鉴定,鉴定证明了那块使人崇敬了多年的裹尸布是假的,它的原料纤维是十三世纪才种出来的,而此时耶稣已被钉在十字架上1200多年了。这个轰动世界的年代鉴定是由研究碳14含量做出的。
一、自学(时间约9分钟)
(1)对数函数的定义:
函数y=logax (a>0且a≠1)叫做对数函数,定义域为(0,+∞),值域为R.
1.温故知新
(2)对数函数的图象和性质
过点(1,0),即当x=1时,y=0
值域: R
定义域:(0,+∞)
a>1 0
性 质
在(0,+∞)上是增函数 在(0,+∞)上是减函数
2.图象和性质的应用
例1.函数y=x+a与y=logax的图象可能是( )
①
②
1
1
O
x
y
1
1
O
x
1
1
O
y
④
③
1
1
O
x
y
③
二、互学(时间约13分钟)
例2:比较下列各组数中两个值的大小:
(1)log67与log76
解:(1)∵ log67>log66=1
且log76<log77=1
∴log67 >log76
(2)log3π与log20.8
(2)∵log3π>log31=0
且log20.8<log21=0
∴log3π>log20.8
(3)log27与log37
(4)log0.20.8 与log0.30.8
(3)
(4)
1.同底数比较大小时
(1)当底数确定时,则可由函数的单调性直接进行判断;
(2)当底数不确定时,应对底数进行分类讨论;
3.若底数、真数都不相同, 则常借助1、0等中间量进行比较
2.同真数的比较大小,常借助函数图象或对数的运算性质变形后进行比较
点评:两个对数比较大小
练习 比较大小
函数x=log2y,y是自变量,x是y的函数,定义域为(0,
+∞),值域为R.
函数y=2x,x是自变量,y是x的函数,定义域为R,
值域为 (0, +∞).
3.探究:对数函数与指数函数之间的关系
这时称函数x=log2y是函数y=2x的反函数.
在函数x=log2y中,y是自变量,x是函数.
三、导学(时间约18分钟)
但是习惯上,通常用x表示自变量,y表示函数.
为此,常常对调函数x=log2y中的字母x与y
把它写成函数y=log2x.
这样对数函数y=log2x与指数函数y=2x互为反函数。
推广 对数函数y=logax与指数函数y=ax互为反函数。
1.设0<x<1,a>0且a≠1,试比较
|loga(1-x)|与|loga(1+x)|的大小。
|loga(1-x)|-|loga(1+x)|=loga(1-x)+loga(1+x)
解:∵0<x<1
∴0<1-x<1,1<1+x<2,0<x2<1
即|loga(1-x)|-|loga(1+x)|>0
∴|loga(1-x)|>|loga(1+x)|
当0
∴ 0<(1-x)(1+x)=1-x2<1
四、检学(时间约5分钟)
|loga(1-x)|-|loga(1+x)|
即|loga(1-x)|-|loga(1+x)|>0
∴ |loga(1-x)|>|loga(1+x)|
当a>1时,则有
=-loga(1-x)-loga(1+x) =-loga(1-x)(1+x)
=- loga(1-x2)>0
当a>1时,有
当0
|loga(1-x)|>|loga(1+x)|.
综上所述,对于0<x<1,a>0 且 a≠1的一切值总有
由以上分类讨论,得
|loga(1-x)|>|loga(1+x)|
2.若函数f(x)=logax (a>0且a≠1)在区间[a, 2a]上的最大值是最小值的3倍,求a的值.
解:当a>1时,f(x)=logax在区间[a,2a]上是增函数,
综上所述, 或
当0
溶液酸碱度是通过pH刻画的. pH的计算公式为
pH=-lg[H+],其中[H+]表示溶液中氢离子的浓度,单位是摩尔/升.
(1)根据对数函数性质及上述pH的计算公式,说明溶液酸碱度与溶液中氢离子的浓度之间的变化关系;
(2)已知纯净水中氢离子的浓度为[H+]=10-7摩尔/升,计算纯净水的pH.
lg[H+]增大,从而-lg[H+]减小,
解:(1)根据对数函数的性质,在(0,+∞)上,随着[H+]的增大,
所以,溶液中氢离子的浓度越大,PH就越小,即溶液的酸性越强。
(2)当[H+] =10-7摩尔/升时,PH=-lg10-7=7,所以,纯净水的PH是7.
于是由PH=-lg[H+]知,PH随着[H+]增大而减小,
1.掌握利用对数函数的性质比较数的大小的方法;
2.对数函数单调性的灵活应用;
3.对数函数与指数函数互为反函数.
作 业
1.将log0.73,log87,0.9-3.1
由小到大排列.
2.已知3lg(x-3)<1, 求x的取值范围.
4.设a>0,且a≠1,比较loga(a2+1)与loga(a3+1)的大小.
3.求下列函数的定义域、值域
