人教版八上数学14.3 因式分解——十字相乘法课件(共32张PPT)
文档属性
| 名称 | 人教版八上数学14.3 因式分解——十字相乘法课件(共32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 311.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-22 00:00:00 | ||
图片预览



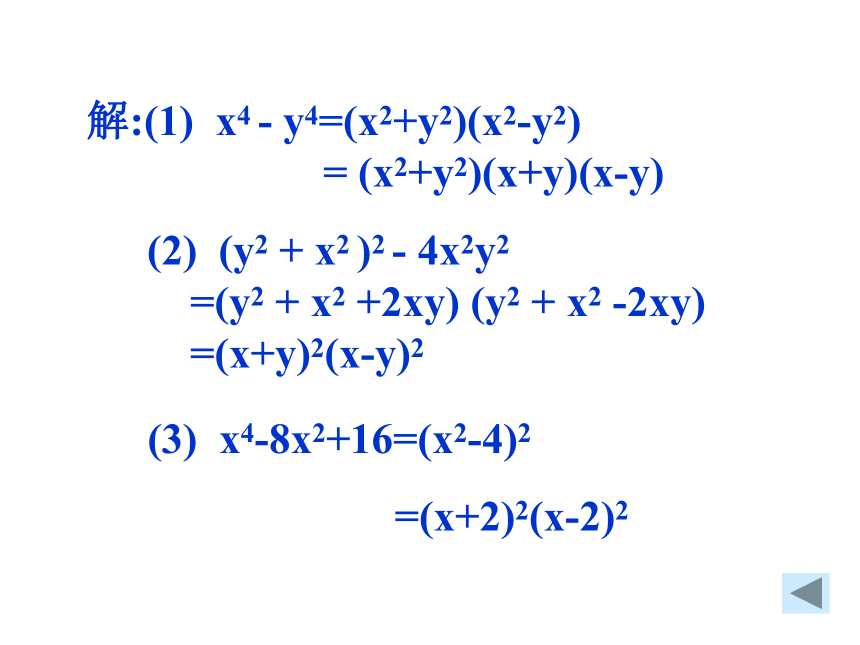
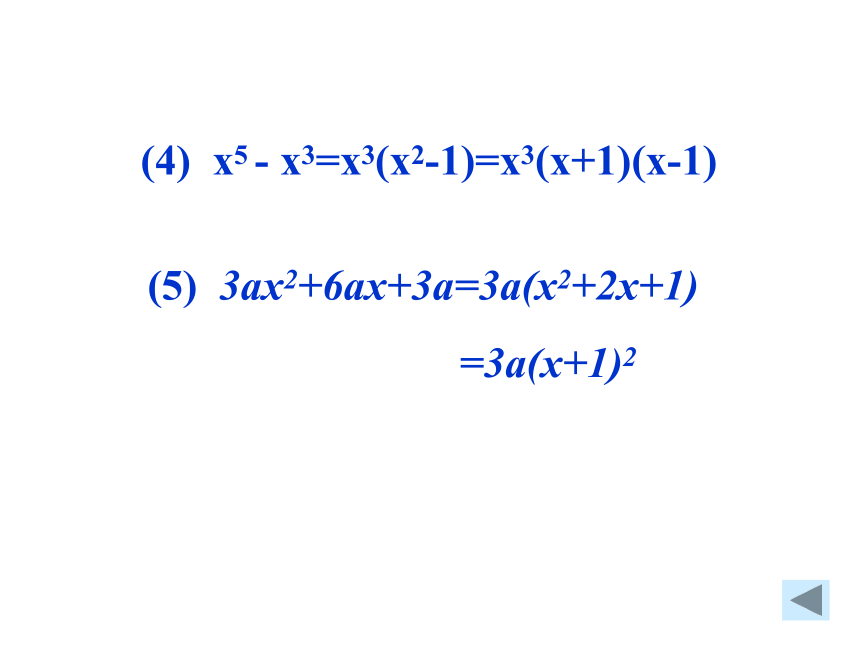


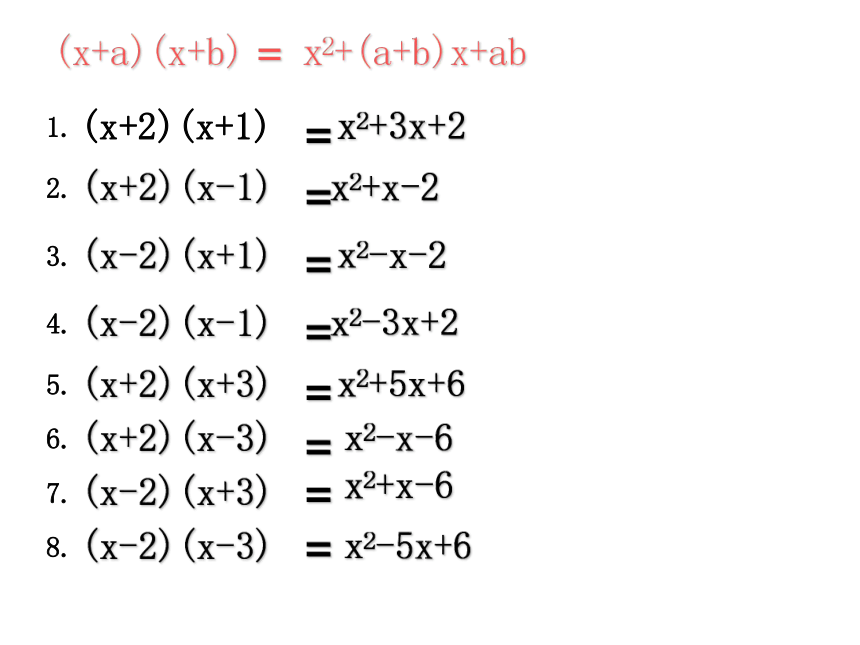




文档简介
(共32张PPT)
因式分解——十字相乘法
知识回顾
1.举例说明因式分解与整式乘法的关系
2.我们已经学习了哪些因式分解的方法?
提公因式法: ma+mb+mc=m(a+b+c)
运用公式法: a2-b2=(a+b)(a-b)
a2 ±2ab+b2=(a ±b)2
(5) 3ax2+6ax+3a
(4) x5 - x3
(1) x4 - y4
(2) (y2 + x2 )2 - 4x2y2
(6) 2ax2+6ax+4a
(3) x4-8x2+16
3.把下列各式因式分解:
解:(1) x4 - y4=(x2+y2)(x2-y2)
= (x2+y2)(x+y)(x-y)
(2) (y2 + x2 )2 - 4x2y2
=(y2 + x2 +2xy) (y2 + x2 -2xy)
=(x+y)2(x-y)2
(3) x4-8x2+16=(x2-4)2
=(x+2)2(x-2)2
(4) x5 - x3=x3(x2-1)=x3(x+1)(x-1)
(5) 3ax2+6ax+3a=3a(x2+2x+1)
=3a(x+1)2
(6) 2ax2+6ax+4a=2a(x2+3x+2)
你认为这个多项式因式还能分解吗?
=2a(x+1)(x+2)
十字相乘法分解因式(1)
1.(x+2)(x+1)=
x2+3x+2
3.(x-2)(x+1)=
x2-x-2
4.(x-2)(x-1)=
x2-3x+2
2.(x+2)(x-1)=
x2+x-2
5.(x+2)(x+3)=
x2+5x+6
6.(x+2)(x-3)=
x2-x-6
7.(x-2)(x+3)=
x2+x-6
8.(x-2)(x-3)=
x2-5x+6
(x+a)(x+b)
=x2+(a+b)x+ab
请直接口答计算结果:
(x+2)(x+1)
x2+3x+2
(x-2)(x+1)
x2-x-2
(x-2)(x-1)
x2-3x+2
(x+2)(x-1)
x2+x-2
(x+2)(x+3)
x2+5x+6
(x+2)(x-3)
x2-x-6
(x-2)(x+3)
x2+x-6
(x-2)(x-3)
x2-5x+6
(x+a)(x+b)
=
x2+(a+b)x+ab
=
=
=
=
=
=
=
=
1.
2.
3.
4.
5.
6.
7.
8.
(x+a)(x+b)=x2+(a+b)x+ab
观察与发现
两个一次二项式相乘的积
一个二次三项式
整式的乘法
反过来,得
x2+(a+b)x+ab=(x+a)(x+b)
一个二次三项式
两个一次二项式相乘的积
因式分解
如果二次三项式x2+px+q中的常数项系数q能分解成两个因数a、b的积,即q=ab而且一次项系数p又恰好是a、b的和,即p=a+b,那么x2+px+q就可以进行如上的因式分解。
分析∵ (+1) ×(+2)=+2
(+1)+(+2)=+3
∴
试一试:把x2+3x+2分解因式
常数项
一次项系数
十字交叉线
利用十字交叉线来分解系数,把二次三项式分解因式的方法叫做十字相乘法。
十字相乘法公式:
请大家记住公式
例1:
分解因式:
x2+4x+3=_______
x2-2x-3=________
(x+3)(x+1)
(x-3)(x+1)
x
x
x
x
3
1
-3
1
练一练
将下列各式用十字相乘法进行因式分解
(1)x2-7x+12 (2)x2-4x-12 (3)x2+8x+12
(4)x2-11x-12 (5)x2+13x+12 (6)x2-x-12
探索规律
对于x2+px+q
(1)当q>0时,a、b﹍﹍,且a、b的符号与p的符号﹍﹍。
(2)当q<0时,a、b﹍﹍,且 ﹍﹍﹍﹍﹍﹍﹍﹍﹍与p的符号相同。
同号
相同
异号
a、b中绝对值较大的因数
例2:试将
分解因式
提示:当二次项系数为-1时 ,先提出负号再因式分解 。
16
6
2
+
-
-
x
x
独立练习:把下列各式分解因式
?
课堂小结
对二次三项式x2+px+q用x2+(a+b)x+ab=(x+a)(x+b)进行因式分解,应重点掌握以下问题:
2.掌握方法:拆分常数项,验证一次项.
3.符号规律:
当q>0时,a、b同号,且a、b的符号与p的符号相同;
当q<0时,a、b异号,且绝对值较大的因数与p的符号相同.
1.适用范围:只有当q=ab,且p=a+b时 才能用十字相乘法进 我 行分解。
用十字相乘法进行因式分解:
(x+2)(x-3)
1.x2-x- 6 =
(x-3)(x+5)
2.x2+2x-15=
(x+2)(x-5)
3.x2-3x-10=
(x-5)(x-4)
4.x2-9x+20=
(x-7)(x+4)
5.x2-3x-28=
(x+2)(x-4)
6.x2-2x-8=
(x-1)(x-3)
7.x2-4x+3=
(x+3)(x+4)
(x+2)(x+3)
(x-3)(x+7)
8.x2+7x+12=
9.x2+5x+6=
10.x2+4x-21=
(y+12)(y-3)
13.y2+9y-36=
(y+4)(y-15)
(y+16)(y+3)
(y+11)(y-10)
(y-13)(y-3)
(y+14)(y+4)
14.y2-11y-60=
15.y2+19y+48=
16.y2+y-110=
17.y2-16y+39=
18.y2+18y+56=
12.x2-11x-12=
(x-12)(x+1)
11.x2+13x+12=
(x+1)(x+12)
比比谁的速度快!
19.x2+(a-1)x-a=
(x+a)(x-1)
20.(x+y) 2+8(x+y)-48=
(x+y+12)(x+y-4)
十字相乘法分解因式(2)
本节课解决两个问题:
第一:对形如ax2+bx+c (a≠0)的二次三项式
进行因式分解;
第二:对形如ax2+bxy+cy2 (a≠0)的二次三项式
进行因式分解;
a2
c1
c2
a1c2+a2c1=b
a1
(a1x+c1) (a2x+c2) =ax2+bx+c (a≠0)
ax2+bx+c=(a1x+c1) (a2x+c2) (a≠0)
整式运算
因式分解
a2
c1
c2
a1c2+a2c1=b
a1
(a1x+c1y) (a2x+c2y) =ax2+bxy+cy2
ax2+bxy+cy2=(a1x+c1y) (a2x+c2y)
整式运算
因式分解
例1:2x2-7x+3
总结:
1、由常数项的符号确定分解的两数的符号
2、由一次项系数确定分解的方向
3、勿忘检验分解的合理性
1
-1
-3
2 × (-3)+(-1) × 1=-7
2
解:原式=(2x-1)(x-3)
例2 分解因式 3x2 -10x+3
解:3x2 -10x+3
x
3x
-3
-1
-9x-x=-10x
=(x-3)(3x-1)
例3 分解因式 5x2-17xy-12y
解:5x2 -17xy-12y2
5x
x
+3y
-4y
-20xy+3xy=-17xy
=(5x+3y)(x-4y)
例4 .将 2(6x2 +x) 2-11(6x2 +x) +5 分解因式
解:2(6x2 +x)2-11(6x2 +x) +5
= [(6x2 +x) -5][2(6x2 +x)-1]
= (6x2 +x-5) (12x2 +2x-1 )
= (6x -5)(x +1) (12x2 +2x-1 )
1
2
-5
-1
-1-10=-11
6
1
-5
1
-5+6=1
练习:将下列各式分解因式
1、 7x -13x+6
2
3、 15x +7xy-4y
2
2
2、 -y -4y+12
2
答案(7x-6)(x-1)
4、 x -(a+1) x+a
2
答案- (y+6)(y-2)
答案 (3x-y)(5x+4y)
答案 (x-1)(x-a)
5、x2+11xy+10y2;
6、2x2-7xy+3y2;
7、-3a2+15ab-12b2;
8、
答案(x+10y)(x+y)
答案 (2x-y)(x-3y)
答案 -3(a-b)(a-4b)
答案 1/4(a-5b)(a+2b)
思考题:把下列各式分解因式
(1)(-x+5y)(3x-y)
(2)(2x-2y+1)(x-y-2)
(1)
(2)
(3)(x+y)2-4(x+y)-5
(4)(m+n)2-5(m+n)+6
=(x+y+1)(x+y-5)
=(m+n-2)(m+n-3)
(5) y2-2y(x-1)-15(x-1)2
=[y+3(x-1)][y-5 (x-1)]
=(y+3x-3)(y-5 x+5)
(6) a2-12a(b+c)+36(b+c)2
=[a-6(b+c)][a-6 (b+c)]
=(a-6b-6c)2
例5 将 2x2-3xy-2y2 +3x+4y-2 分解因式
解: 2x -3xy-2y +3x+4y-2
2
2
=(2x -3xy-2y )+3x+4y-2
2
2
=(2x +y)(x-2y)+3x+4y-2
=(2x +y-1)(x-2y+2)
2
1
1
-2
-4+1=-3
(2x+y)
(x-2y)
-1
2
2(2x+y) - (x- 2 y)=3x+4y
例6. 分解因式(x2+2x)2-2(x2+2x)-3.
【解】(x2+2x)2-2(x2+2x)-3
=(x2+2x-3)(x2+2x+1)
=(x+3)(x-1)(x+1)2.
(x2+2x)
(x2+2x)
-3
1
-3(x2+2x) + (x2+2x)=-2x2- 4x
1
1
3
-1
-1+3=2
2.将2x2-7xy-22y2-5x+35y-3分解因式
1.将(a2+8a)2+22(a2+8a)+120分解因式
3.因式分解:
(1)x2-3xy-10y2+x+9y-2;
(2)x2-y2+5x+3y+4;
(3)xy+y2+x-y-2;
(4)6x2-7xy-3y2-xz+7yz-2z2
因式分解——十字相乘法
知识回顾
1.举例说明因式分解与整式乘法的关系
2.我们已经学习了哪些因式分解的方法?
提公因式法: ma+mb+mc=m(a+b+c)
运用公式法: a2-b2=(a+b)(a-b)
a2 ±2ab+b2=(a ±b)2
(5) 3ax2+6ax+3a
(4) x5 - x3
(1) x4 - y4
(2) (y2 + x2 )2 - 4x2y2
(6) 2ax2+6ax+4a
(3) x4-8x2+16
3.把下列各式因式分解:
解:(1) x4 - y4=(x2+y2)(x2-y2)
= (x2+y2)(x+y)(x-y)
(2) (y2 + x2 )2 - 4x2y2
=(y2 + x2 +2xy) (y2 + x2 -2xy)
=(x+y)2(x-y)2
(3) x4-8x2+16=(x2-4)2
=(x+2)2(x-2)2
(4) x5 - x3=x3(x2-1)=x3(x+1)(x-1)
(5) 3ax2+6ax+3a=3a(x2+2x+1)
=3a(x+1)2
(6) 2ax2+6ax+4a=2a(x2+3x+2)
你认为这个多项式因式还能分解吗?
=2a(x+1)(x+2)
十字相乘法分解因式(1)
1.(x+2)(x+1)=
x2+3x+2
3.(x-2)(x+1)=
x2-x-2
4.(x-2)(x-1)=
x2-3x+2
2.(x+2)(x-1)=
x2+x-2
5.(x+2)(x+3)=
x2+5x+6
6.(x+2)(x-3)=
x2-x-6
7.(x-2)(x+3)=
x2+x-6
8.(x-2)(x-3)=
x2-5x+6
(x+a)(x+b)
=x2+(a+b)x+ab
请直接口答计算结果:
(x+2)(x+1)
x2+3x+2
(x-2)(x+1)
x2-x-2
(x-2)(x-1)
x2-3x+2
(x+2)(x-1)
x2+x-2
(x+2)(x+3)
x2+5x+6
(x+2)(x-3)
x2-x-6
(x-2)(x+3)
x2+x-6
(x-2)(x-3)
x2-5x+6
(x+a)(x+b)
=
x2+(a+b)x+ab
=
=
=
=
=
=
=
=
1.
2.
3.
4.
5.
6.
7.
8.
(x+a)(x+b)=x2+(a+b)x+ab
观察与发现
两个一次二项式相乘的积
一个二次三项式
整式的乘法
反过来,得
x2+(a+b)x+ab=(x+a)(x+b)
一个二次三项式
两个一次二项式相乘的积
因式分解
如果二次三项式x2+px+q中的常数项系数q能分解成两个因数a、b的积,即q=ab而且一次项系数p又恰好是a、b的和,即p=a+b,那么x2+px+q就可以进行如上的因式分解。
分析∵ (+1) ×(+2)=+2
(+1)+(+2)=+3
∴
试一试:把x2+3x+2分解因式
常数项
一次项系数
十字交叉线
利用十字交叉线来分解系数,把二次三项式分解因式的方法叫做十字相乘法。
十字相乘法公式:
请大家记住公式
例1:
分解因式:
x2+4x+3=_______
x2-2x-3=________
(x+3)(x+1)
(x-3)(x+1)
x
x
x
x
3
1
-3
1
练一练
将下列各式用十字相乘法进行因式分解
(1)x2-7x+12 (2)x2-4x-12 (3)x2+8x+12
(4)x2-11x-12 (5)x2+13x+12 (6)x2-x-12
探索规律
对于x2+px+q
(1)当q>0时,a、b﹍﹍,且a、b的符号与p的符号﹍﹍。
(2)当q<0时,a、b﹍﹍,且 ﹍﹍﹍﹍﹍﹍﹍﹍﹍与p的符号相同。
同号
相同
异号
a、b中绝对值较大的因数
例2:试将
分解因式
提示:当二次项系数为-1时 ,先提出负号再因式分解 。
16
6
2
+
-
-
x
x
独立练习:把下列各式分解因式
?
课堂小结
对二次三项式x2+px+q用x2+(a+b)x+ab=(x+a)(x+b)进行因式分解,应重点掌握以下问题:
2.掌握方法:拆分常数项,验证一次项.
3.符号规律:
当q>0时,a、b同号,且a、b的符号与p的符号相同;
当q<0时,a、b异号,且绝对值较大的因数与p的符号相同.
1.适用范围:只有当q=ab,且p=a+b时 才能用十字相乘法进 我 行分解。
用十字相乘法进行因式分解:
(x+2)(x-3)
1.x2-x- 6 =
(x-3)(x+5)
2.x2+2x-15=
(x+2)(x-5)
3.x2-3x-10=
(x-5)(x-4)
4.x2-9x+20=
(x-7)(x+4)
5.x2-3x-28=
(x+2)(x-4)
6.x2-2x-8=
(x-1)(x-3)
7.x2-4x+3=
(x+3)(x+4)
(x+2)(x+3)
(x-3)(x+7)
8.x2+7x+12=
9.x2+5x+6=
10.x2+4x-21=
(y+12)(y-3)
13.y2+9y-36=
(y+4)(y-15)
(y+16)(y+3)
(y+11)(y-10)
(y-13)(y-3)
(y+14)(y+4)
14.y2-11y-60=
15.y2+19y+48=
16.y2+y-110=
17.y2-16y+39=
18.y2+18y+56=
12.x2-11x-12=
(x-12)(x+1)
11.x2+13x+12=
(x+1)(x+12)
比比谁的速度快!
19.x2+(a-1)x-a=
(x+a)(x-1)
20.(x+y) 2+8(x+y)-48=
(x+y+12)(x+y-4)
十字相乘法分解因式(2)
本节课解决两个问题:
第一:对形如ax2+bx+c (a≠0)的二次三项式
进行因式分解;
第二:对形如ax2+bxy+cy2 (a≠0)的二次三项式
进行因式分解;
a2
c1
c2
a1c2+a2c1=b
a1
(a1x+c1) (a2x+c2) =ax2+bx+c (a≠0)
ax2+bx+c=(a1x+c1) (a2x+c2) (a≠0)
整式运算
因式分解
a2
c1
c2
a1c2+a2c1=b
a1
(a1x+c1y) (a2x+c2y) =ax2+bxy+cy2
ax2+bxy+cy2=(a1x+c1y) (a2x+c2y)
整式运算
因式分解
例1:2x2-7x+3
总结:
1、由常数项的符号确定分解的两数的符号
2、由一次项系数确定分解的方向
3、勿忘检验分解的合理性
1
-1
-3
2 × (-3)+(-1) × 1=-7
2
解:原式=(2x-1)(x-3)
例2 分解因式 3x2 -10x+3
解:3x2 -10x+3
x
3x
-3
-1
-9x-x=-10x
=(x-3)(3x-1)
例3 分解因式 5x2-17xy-12y
解:5x2 -17xy-12y2
5x
x
+3y
-4y
-20xy+3xy=-17xy
=(5x+3y)(x-4y)
例4 .将 2(6x2 +x) 2-11(6x2 +x) +5 分解因式
解:2(6x2 +x)2-11(6x2 +x) +5
= [(6x2 +x) -5][2(6x2 +x)-1]
= (6x2 +x-5) (12x2 +2x-1 )
= (6x -5)(x +1) (12x2 +2x-1 )
1
2
-5
-1
-1-10=-11
6
1
-5
1
-5+6=1
练习:将下列各式分解因式
1、 7x -13x+6
2
3、 15x +7xy-4y
2
2
2、 -y -4y+12
2
答案(7x-6)(x-1)
4、 x -(a+1) x+a
2
答案- (y+6)(y-2)
答案 (3x-y)(5x+4y)
答案 (x-1)(x-a)
5、x2+11xy+10y2;
6、2x2-7xy+3y2;
7、-3a2+15ab-12b2;
8、
答案(x+10y)(x+y)
答案 (2x-y)(x-3y)
答案 -3(a-b)(a-4b)
答案 1/4(a-5b)(a+2b)
思考题:把下列各式分解因式
(1)(-x+5y)(3x-y)
(2)(2x-2y+1)(x-y-2)
(1)
(2)
(3)(x+y)2-4(x+y)-5
(4)(m+n)2-5(m+n)+6
=(x+y+1)(x+y-5)
=(m+n-2)(m+n-3)
(5) y2-2y(x-1)-15(x-1)2
=[y+3(x-1)][y-5 (x-1)]
=(y+3x-3)(y-5 x+5)
(6) a2-12a(b+c)+36(b+c)2
=[a-6(b+c)][a-6 (b+c)]
=(a-6b-6c)2
例5 将 2x2-3xy-2y2 +3x+4y-2 分解因式
解: 2x -3xy-2y +3x+4y-2
2
2
=(2x -3xy-2y )+3x+4y-2
2
2
=(2x +y)(x-2y)+3x+4y-2
=(2x +y-1)(x-2y+2)
2
1
1
-2
-4+1=-3
(2x+y)
(x-2y)
-1
2
2(2x+y) - (x- 2 y)=3x+4y
例6. 分解因式(x2+2x)2-2(x2+2x)-3.
【解】(x2+2x)2-2(x2+2x)-3
=(x2+2x-3)(x2+2x+1)
=(x+3)(x-1)(x+1)2.
(x2+2x)
(x2+2x)
-3
1
-3(x2+2x) + (x2+2x)=-2x2- 4x
1
1
3
-1
-1+3=2
2.将2x2-7xy-22y2-5x+35y-3分解因式
1.将(a2+8a)2+22(a2+8a)+120分解因式
3.因式分解:
(1)x2-3xy-10y2+x+9y-2;
(2)x2-y2+5x+3y+4;
(3)xy+y2+x-y-2;
(4)6x2-7xy-3y2-xz+7yz-2z2
