沪教数学八上19.2 证明举例课件(18张PPT)
文档属性
| 名称 | 沪教数学八上19.2 证明举例课件(18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 676.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-23 07:52:23 | ||
图片预览






文档简介
课件18张PPT。多一些思考,让想法变得更加清澈§19.2 证明举例一、课前回顾(自我整理)1、在前段时间的几何证明学习过程中我们学习或
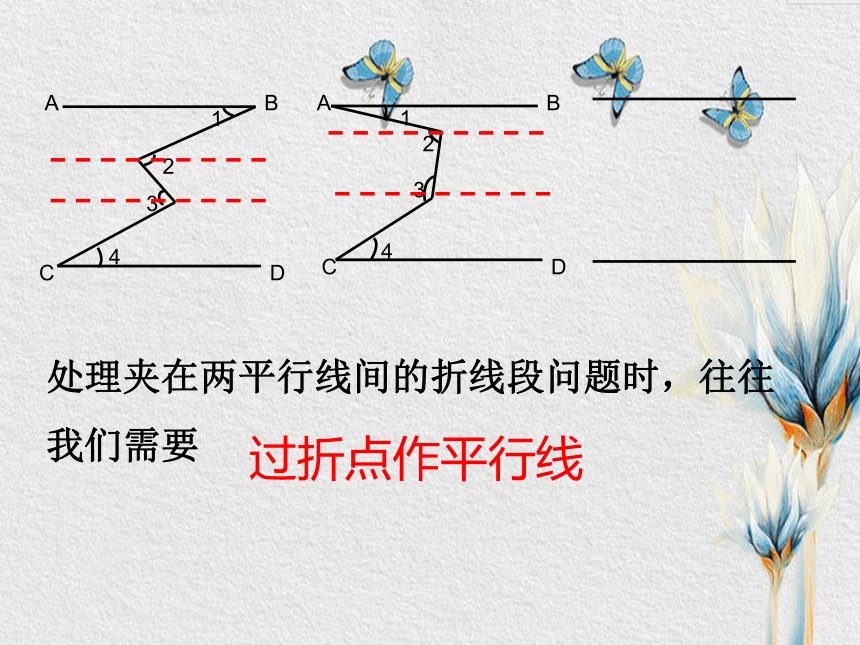
复习了哪些相关知识?2、熟记并掌握一些常见的基本图形及其构造ABCDEFGHABCDEFGH处理夹在两平行线间的折线段问题时,往往
我们需要过折点作平行线ABCA1B1还有更多的一些基本图形…3、几何证明中我们常涉及的两类基本问题
(1)数量关系:线段、角
(2)位置关系:直线(线段) 相等、和、差、倍、分平行、垂直证明真命题的步骤:(1)根据题意做出图形,并在图中标出必要的字母和符号;
(2)根据题设和结论,结合图形,写出“已知”和“求证”;
(3)经过分析,找出由已知推出结论的途径,写出证明过程.证明假命题的方法——举出一个反例4、如何证明一个命题是真命题还是假命题?二、例题分析例1、如图,在四边形ABCD中,AD∥BC,E是AB的
中点,联结DE并延长交CB的延长线于点F,点G在边
BC上,且 (1)求证:(2)联结EG,判断EG与DF的
位置关系并证明
例2、如图,在正方形ABCD中,求证:EF=AE+FCABCDEFG辅助线:延长DA至点G,使AG=CF,
联结BG例2、如图,在正方形ABCD中,求证:EF=AE+FCABCDEFH辅助线:延长DC至点H,使CH=AE,
联结BH例3、求证:有两边及其中一边上的中线对应相等的两个三角形全等ABCA′B′C′DD′已知:如图,在△ABC与△A′B′C′中,AD、A′D′分别是BC、B′C′上的中线,AB=A′B′,BC=B′C′,AD=A′D′
求证:△ABC≌△A′B′C′思考:若将上述命题改为“有两边及第三边上的中线对应相等的两个三角形全等”则该命题为真命题还是假命题你还可以进一步思考:三、课堂练习练习1、如图,是边长为1的等边三角形,是顶角为的等腰三角形,以D为顶点作一个角,角的两边分别交AB于M,交AC于N,联结MN,求的周长形成一个ABCDMNE分析:练习2、
已知如图,在(不与B、C两点重合),点F在边CA的延长线上,且
AF=BE,联结EF交AB于点D
求证:DE=DFACBEFDG辅助线:过点E作EG//AC,交AB于点G命题1:有两边及其中一边上的高对应相等的
两个三角形全等你还有怎样的想法:命题2:有两边及第三边上的高对应相等的
两个三角形全等四、总结、归纳(自我提升)写下你的收获与体会…谢谢!
复习了哪些相关知识?2、熟记并掌握一些常见的基本图形及其构造ABCDEFGHABCDEFGH处理夹在两平行线间的折线段问题时,往往
我们需要过折点作平行线ABCA1B1还有更多的一些基本图形…3、几何证明中我们常涉及的两类基本问题
(1)数量关系:线段、角
(2)位置关系:直线(线段) 相等、和、差、倍、分平行、垂直证明真命题的步骤:(1)根据题意做出图形,并在图中标出必要的字母和符号;
(2)根据题设和结论,结合图形,写出“已知”和“求证”;
(3)经过分析,找出由已知推出结论的途径,写出证明过程.证明假命题的方法——举出一个反例4、如何证明一个命题是真命题还是假命题?二、例题分析例1、如图,在四边形ABCD中,AD∥BC,E是AB的
中点,联结DE并延长交CB的延长线于点F,点G在边
BC上,且 (1)求证:(2)联结EG,判断EG与DF的
位置关系并证明
例2、如图,在正方形ABCD中,求证:EF=AE+FCABCDEFG辅助线:延长DA至点G,使AG=CF,
联结BG例2、如图,在正方形ABCD中,求证:EF=AE+FCABCDEFH辅助线:延长DC至点H,使CH=AE,
联结BH例3、求证:有两边及其中一边上的中线对应相等的两个三角形全等ABCA′B′C′DD′已知:如图,在△ABC与△A′B′C′中,AD、A′D′分别是BC、B′C′上的中线,AB=A′B′,BC=B′C′,AD=A′D′
求证:△ABC≌△A′B′C′思考:若将上述命题改为“有两边及第三边上的中线对应相等的两个三角形全等”则该命题为真命题还是假命题你还可以进一步思考:三、课堂练习练习1、如图,是边长为1的等边三角形,是顶角为的等腰三角形,以D为顶点作一个角,角的两边分别交AB于M,交AC于N,联结MN,求的周长形成一个ABCDMNE分析:练习2、
已知如图,在(不与B、C两点重合),点F在边CA的延长线上,且
AF=BE,联结EF交AB于点D
求证:DE=DFACBEFDG辅助线:过点E作EG//AC,交AB于点G命题1:有两边及其中一边上的高对应相等的
两个三角形全等你还有怎样的想法:命题2:有两边及第三边上的高对应相等的
两个三角形全等四、总结、归纳(自我提升)写下你的收获与体会…谢谢!
