人教版选修1-2 1.1.2 独立性检验的基本思想及其初步应用课件(19张)
文档属性
| 名称 | 人教版选修1-2 1.1.2 独立性检验的基本思想及其初步应用课件(19张) |

|
|
| 格式 | zip | ||
| 文件大小 | 79.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-22 00:00:00 | ||
图片预览





文档简介
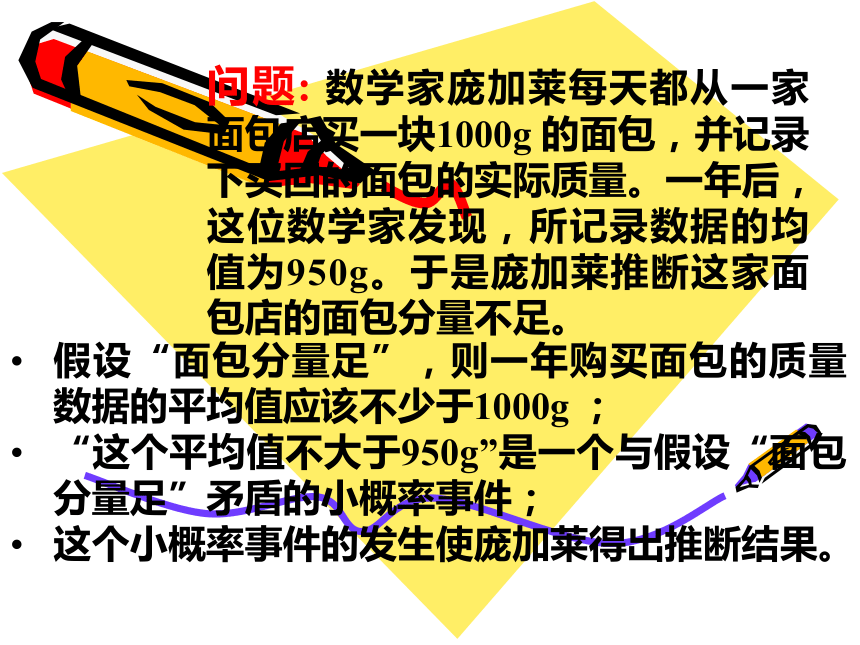
课件19张PPT。独立性检验的基本思想及其初步应用 问题: 数学家庞加莱每天都从一家面包店买一块1000g 的面包,并记录下买回的面包的实际质量。一年后,这位数学家发现,所记录数据的均值为950g。于是庞加莱推断这家面包店的面包分量不足。假设“面包分量足”,则一年购买面包的质量数据的平均值应该不少于1000g ;
“这个平均值不大于950g”是一个与假设“面包分量足”矛盾的小概率事件;
这个小概率事件的发生使庞加莱得出推断结果。一:假设检验问题的原理假设检验问题由两个互斥的假设构成,其中一个
叫做原假设,用H0表示;另一个叫做备择假设,用H1表示。例如,在前面的例子中, 原假设为: H0:面包分量足,
备择假设为 H1:面包分量不足。
这个假设检验问题可以表达为:
H0:面包分量足 ←→ H1:面包分量不足
二:求解假设检验问题考虑假设检验问题:
H0:面包分量足 ←→ H1:面包分量不足在H0成立的条件下,构造与H0矛盾的小概率事件;
如果样本使得这个小概率事件发生,就能以一定把握断言H1成立;否则,断言没有发现样本数据与H0相矛盾的证据。
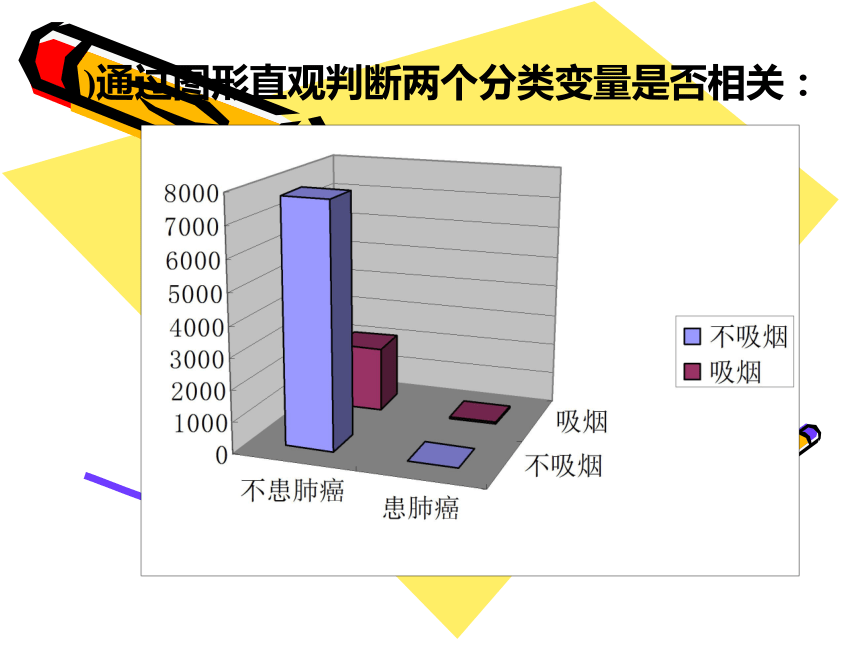
求解思路:三:二个概念这种变量的不同取“值”表示个体所属的不同类别,这类变量称为分类变量1.分类变量 对于性别变量,取值为:男、女 分类变量在现实生活中是大量存在的,如是否吸烟,是否患肺癌,宗教信仰,国别,年龄,出生月份等等。利用随机变量K2来确定在多大程度上可以认为”两个分类变量有关系”的方法称为两个分类变量的独立性检验.(为假设检验的特例)问题:为了调查吸烟是否对肺癌有影响,某肿瘤研究所随机地调查了9965人,得到如下结果(单位:人)说明:吸烟者和不吸烟者患肺癌的可能性存在差异,吸烟者患肺癌的可能性大0.54%2.28%1)通过图形直观判断两个分类变量是否相关:
2) 通过图形直观判断两个分类变量是否相关:
3)通过图形直观判断两个分类变量是否相关:
患肺癌
比例不患肺癌
比例 独立性检验H0: 吸烟和患肺癌之间没有关系
←→ H1: 吸烟和患肺癌之间有关系通过数据和图表分析,得到结论是:吸烟与患肺癌有关用 A 表示“不吸烟”, B 表示“不患肺癌”则 H0: 吸烟和患肺癌之间没有关系 “吸烟”与“患肺癌”独立,即A与B独立等价于等价于 独立性检验引入一个随机变量作为检验在多大程度上可以认为“两个变量有关系”的标准 。设有两个分类变量X和Y它们的值域分别为{x1,x2}和{y1,y2}其样本频数列表(称为2×2列联表) 为2×2列联表 独立性检验通过公式计算 独立性检验现在的K2=56.632的观测值远大于6.635分类变量之间关系条形图柱形图列联表独立性检验背景分析例1.在某医院,因为患心脏病而住院的665名男性病人中,有214人秃顶,而另外772名不是因为患心脏病而住院的男性病人中有175人秃顶.分别利用图形和独立性检验方法判断是否有关?你所得的结论在什么范围内有效?例2.为考察高中生性别与是否喜欢数学课程之间的关系,在某城市的某校高中生中随机抽取300名学生,得到如下列联表: 性别与喜欢数学课程列联表acdb解:P111独立性检验基本的思想类似反证法(1)假设结论不成立,即“两个分类变量没有关系”.
(2)在此假设下随机变量 K2 应该很能小,如果由观测数据
计算得到K2的观测值k很大,则在一定程度上说明假设
不合理.
(3)根据随机变量K2的含义,可以通过
评价该假设不合理的程度,由实际计算出的,
说明假设合理的程度为99.9%,即“两个分类变量有关系”这一结论成立的可信度为约为99.9%.
“这个平均值不大于950g”是一个与假设“面包分量足”矛盾的小概率事件;
这个小概率事件的发生使庞加莱得出推断结果。一:假设检验问题的原理假设检验问题由两个互斥的假设构成,其中一个
叫做原假设,用H0表示;另一个叫做备择假设,用H1表示。例如,在前面的例子中, 原假设为: H0:面包分量足,
备择假设为 H1:面包分量不足。
这个假设检验问题可以表达为:
H0:面包分量足 ←→ H1:面包分量不足
二:求解假设检验问题考虑假设检验问题:
H0:面包分量足 ←→ H1:面包分量不足在H0成立的条件下,构造与H0矛盾的小概率事件;
如果样本使得这个小概率事件发生,就能以一定把握断言H1成立;否则,断言没有发现样本数据与H0相矛盾的证据。
求解思路:三:二个概念这种变量的不同取“值”表示个体所属的不同类别,这类变量称为分类变量1.分类变量 对于性别变量,取值为:男、女 分类变量在现实生活中是大量存在的,如是否吸烟,是否患肺癌,宗教信仰,国别,年龄,出生月份等等。利用随机变量K2来确定在多大程度上可以认为”两个分类变量有关系”的方法称为两个分类变量的独立性检验.(为假设检验的特例)问题:为了调查吸烟是否对肺癌有影响,某肿瘤研究所随机地调查了9965人,得到如下结果(单位:人)说明:吸烟者和不吸烟者患肺癌的可能性存在差异,吸烟者患肺癌的可能性大0.54%2.28%1)通过图形直观判断两个分类变量是否相关:
2) 通过图形直观判断两个分类变量是否相关:
3)通过图形直观判断两个分类变量是否相关:
患肺癌
比例不患肺癌
比例 独立性检验H0: 吸烟和患肺癌之间没有关系
←→ H1: 吸烟和患肺癌之间有关系通过数据和图表分析,得到结论是:吸烟与患肺癌有关用 A 表示“不吸烟”, B 表示“不患肺癌”则 H0: 吸烟和患肺癌之间没有关系 “吸烟”与“患肺癌”独立,即A与B独立等价于等价于 独立性检验引入一个随机变量作为检验在多大程度上可以认为“两个变量有关系”的标准 。设有两个分类变量X和Y它们的值域分别为{x1,x2}和{y1,y2}其样本频数列表(称为2×2列联表) 为2×2列联表 独立性检验通过公式计算 独立性检验现在的K2=56.632的观测值远大于6.635分类变量之间关系条形图柱形图列联表独立性检验背景分析例1.在某医院,因为患心脏病而住院的665名男性病人中,有214人秃顶,而另外772名不是因为患心脏病而住院的男性病人中有175人秃顶.分别利用图形和独立性检验方法判断是否有关?你所得的结论在什么范围内有效?例2.为考察高中生性别与是否喜欢数学课程之间的关系,在某城市的某校高中生中随机抽取300名学生,得到如下列联表: 性别与喜欢数学课程列联表acdb解:P111独立性检验基本的思想类似反证法(1)假设结论不成立,即“两个分类变量没有关系”.
(2)在此假设下随机变量 K2 应该很能小,如果由观测数据
计算得到K2的观测值k很大,则在一定程度上说明假设
不合理.
(3)根据随机变量K2的含义,可以通过
评价该假设不合理的程度,由实际计算出的,
说明假设合理的程度为99.9%,即“两个分类变量有关系”这一结论成立的可信度为约为99.9%.
