人教版选修1-2 2.1.2演绎推理课件(15张)
文档属性
| 名称 | 人教版选修1-2 2.1.2演绎推理课件(15张) |

|
|
| 格式 | zip | ||
| 文件大小 | 331.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-22 17:04:46 | ||
图片预览




文档简介
课件15张PPT。2.1.2 演绎推理复习:合情推理归纳推理
类比推理从具体问题出发观察、分析
比较、联想提出猜想归纳、
类比类比推理的一般步骤:⑴ 找出两类对象之间可以确切表述的相似特征;
⑵ 用一类对象的已知特征去推测另一类对象的特征,从而得出一个猜想;
⑶ 检验猜想。 复习:合情推理⑴ 对有限的资料进行观察、分析、归纳 整理;
⑵ 提出带有规律性的结论,即猜想;
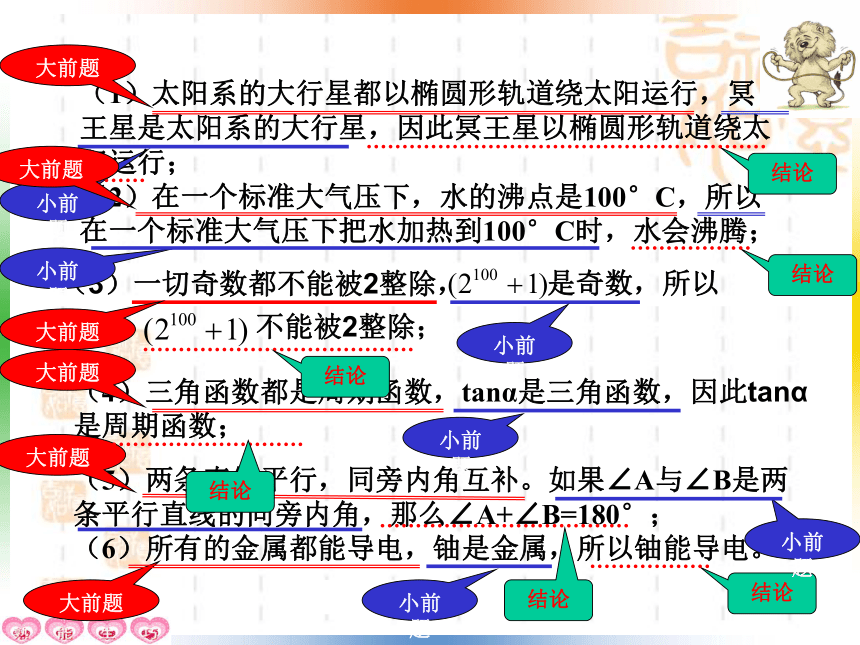
⑶ 检验猜想。 归纳推理的一般步骤:演绎推理的一般模式:大前提:鱼类、贝类、鱼龙,都是海洋生物,它们世世代代生活在海洋里 小前提:在喜马拉雅山上发现它们的化石 结论:喜马拉雅山曾经是海洋 喜马拉雅山所在的地方,曾经是一片汪洋推理过程: (1)大前提……已知的一般原理(2)小前提……所研究的特殊情况(3)结论………根据一般原理,对特殊情况作出的判断三段论演绎推理:从一般性的原理出发,推出某个特殊情况下的结论的推理方法。从一般性的原理出发,推出某个特殊情况下的结论,我们把这种推理称为演绎推理(1)太阳系的大行星都以椭圆形轨道绕太阳运行,冥王星是太阳系的大行星,因此冥王星以椭圆形轨道绕太阳运行;
(2)在一个标准大气压下,水的沸点是100°C,所以在一个标准大气压下把水加热到100°C时,水会沸腾;(4)三角函数都是周期函数,tanα是三角函数,因此tanα是周期函数;(5)两条直线平行,同旁内角互补。如果∠A与∠B是两条平行直线的同旁内角,那么∠A+∠B=180°;
(6)所有的金属都能导电,铀是金属,所以铀能导电。 (1)大前提……已知的一般原理(2)小前提……所研究的特殊情况
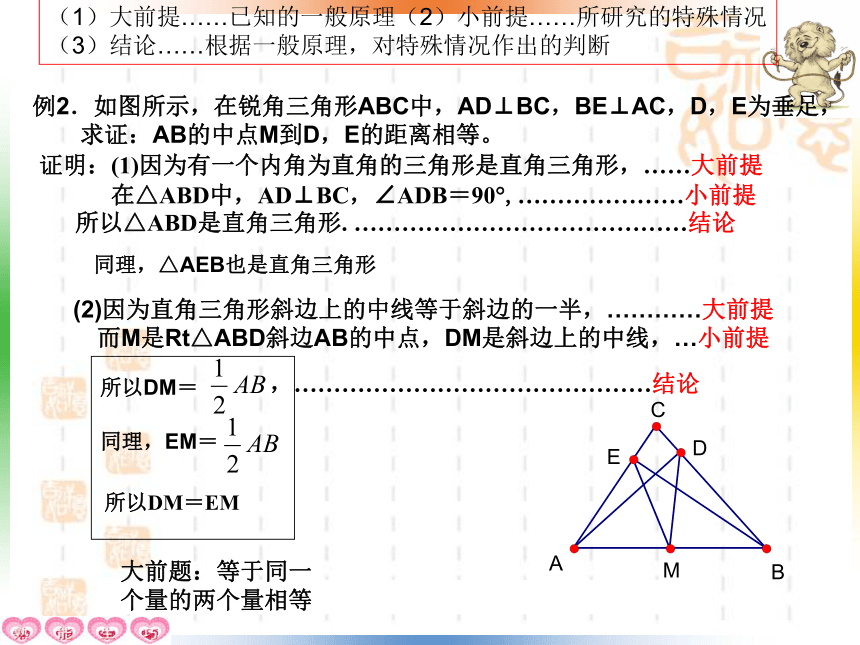
(3)结论……根据一般原理,对特殊情况作出的判断 例2.如图所示,在锐角三角形ABC中,AD⊥BC,BE⊥AC,D,E为垂足,
求证:AB的中点M到D,E的距离相等。 证明:(1)因为有一个内角为直角的三角形是直角三角形,……大前提
在△ABD中,AD⊥BC,∠ADB=90?,…………………小前提
所以△ABD是直角三角形. ……………………………………结论所以DM=EM 同理,EM=(2)因为直角三角形斜边上的中线等于斜边的一半,…………大前提
而M是Rt△ABD斜边AB的中点,DM是斜边上的中线,…小前提同理,△AEB也是直角三角形大前题:等于同一个量的两个量相等 用三段论证明:通项公式为 的数列为等比数列。 证明:,如果一个数列从第2项起,每一项与它的前一项的比等于同一常数,那么这个数列叫做等比数列 ……… ………大前题q是常数………小前题通项公式为 的数列为等比数列…………结论(1)大前提……已知的一般原理(2)小前提……所研究的特殊情况
(3)结论……根据一般原理,对特殊情况作出的判断 用集合论的观点分析:若集合M中的所有元素都具有性质P,S是M的一个子集,那么S中所有元素也都具有性质P。 “三段论”可以表示为
大前题:M是P 小前提:S是M 结论:S是P。 (1)大前提……已知的一般原理(2)小前提……所研究的特殊情况
(3)结论……根据一般原理,对特殊情况作出的判断 MS大前题不正确推理形式 错误无限小数无限小数 ππ(1)大前提……已知的一般原理(2)小前提……所研究的特殊情况
(3)结论……根据一般原理,对特殊情况作出的判断 用三段论证明:函数f(x)=-x2+2x在(-∞,1]上是增函数。 大前提:增函数的定义
小前提:f(x)在(-∞,1]上满足定义
结论: f(x)在(-∞,1]上是增函数大前提:在区间(a,b)上如果f ’(x)>0,那么函
数y=f(x)在这个区间内单调递增
小前提:f(x)=-x2+2x在(-∞,1)上有f ‘(x)>0
结论: f(x)在(-∞,1]上是增函数(1)大前提……已知的一般原理(2)小前提……所研究的特殊情况
(3)结论……根据一般原理,对特殊情况作出的判断 归纳是由部分到整体、个体到一般的推理;类比推理是由特殊到特殊的推理由一般到特殊的推理不一定正确,有待于进一步证明大前提、小前提和推理形式都正确的前提下,得到的结论一定正确需要通过观察、实验等获取经验辨别它们的真伪,或将积累的知识加工、整理,使之条理化,系统化证明数学结论、建立数学体系的重要思维过程数学结论、证明思路等的发现 用三段论证明:若梯形的两个腰和一个底如果相等,它的对角线必平分另一底上的两个角。 证明:若三角形有两边相等,则三角形是等腰三角形………大前题
∵AD=DC …………………………………小前题
∴三角形ADC是等腰三角形………………结论等腰三角形的两底角相等………大前题
∵三角形ADC是等腰三角形,AD和DC是两腰………小前题
∴∠DAC= ∠DCA ………………结论两直线平行,内错角相等………大前题
∵∠DAC和∠ACB是AD∥BC的内错角………小前题
∴∠DAC=∠ACB ……… ………结论等于同一个量的两个量相等……………大前题
∴∠DCA和∠ACB都等于∠DAC ………小前题
∴∠DCA=∠ACB ………………………结论
∴AC平分∠DCB 同理, BD平分∠ABC 课堂小结:
1.俗话说,打鱼人识不完鱼,庄稼人识不完草。认识事物的任务十分艰巨,把握规律的道路分外漫长。我们不能事事去亲知,事事去实验。但是我们运用这种演绎方法,你就能以一知十,以近知远,以少知多。演绎推理还使人们产生新的创意或新的发现。
2.演绎方法是一种重要的认识工具,也是科学发现的有用方法。我们面前,一个无限广阔的世界正等待我们去认识,等待着我们去利用,去改造。(1)大前提……已知的一般原理(2)小前提……所研究的特殊情况
(3)结论……根据一般原理,对特殊情况作出的判断 结束
类比推理从具体问题出发观察、分析
比较、联想提出猜想归纳、
类比类比推理的一般步骤:⑴ 找出两类对象之间可以确切表述的相似特征;
⑵ 用一类对象的已知特征去推测另一类对象的特征,从而得出一个猜想;
⑶ 检验猜想。 复习:合情推理⑴ 对有限的资料进行观察、分析、归纳 整理;
⑵ 提出带有规律性的结论,即猜想;
⑶ 检验猜想。 归纳推理的一般步骤:演绎推理的一般模式:大前提:鱼类、贝类、鱼龙,都是海洋生物,它们世世代代生活在海洋里 小前提:在喜马拉雅山上发现它们的化石 结论:喜马拉雅山曾经是海洋 喜马拉雅山所在的地方,曾经是一片汪洋推理过程: (1)大前提……已知的一般原理(2)小前提……所研究的特殊情况(3)结论………根据一般原理,对特殊情况作出的判断三段论演绎推理:从一般性的原理出发,推出某个特殊情况下的结论的推理方法。从一般性的原理出发,推出某个特殊情况下的结论,我们把这种推理称为演绎推理(1)太阳系的大行星都以椭圆形轨道绕太阳运行,冥王星是太阳系的大行星,因此冥王星以椭圆形轨道绕太阳运行;
(2)在一个标准大气压下,水的沸点是100°C,所以在一个标准大气压下把水加热到100°C时,水会沸腾;(4)三角函数都是周期函数,tanα是三角函数,因此tanα是周期函数;(5)两条直线平行,同旁内角互补。如果∠A与∠B是两条平行直线的同旁内角,那么∠A+∠B=180°;
(6)所有的金属都能导电,铀是金属,所以铀能导电。 (1)大前提……已知的一般原理(2)小前提……所研究的特殊情况
(3)结论……根据一般原理,对特殊情况作出的判断 例2.如图所示,在锐角三角形ABC中,AD⊥BC,BE⊥AC,D,E为垂足,
求证:AB的中点M到D,E的距离相等。 证明:(1)因为有一个内角为直角的三角形是直角三角形,……大前提
在△ABD中,AD⊥BC,∠ADB=90?,…………………小前提
所以△ABD是直角三角形. ……………………………………结论所以DM=EM 同理,EM=(2)因为直角三角形斜边上的中线等于斜边的一半,…………大前提
而M是Rt△ABD斜边AB的中点,DM是斜边上的中线,…小前提同理,△AEB也是直角三角形大前题:等于同一个量的两个量相等 用三段论证明:通项公式为 的数列为等比数列。 证明:,如果一个数列从第2项起,每一项与它的前一项的比等于同一常数,那么这个数列叫做等比数列 ……… ………大前题q是常数………小前题通项公式为 的数列为等比数列…………结论(1)大前提……已知的一般原理(2)小前提……所研究的特殊情况
(3)结论……根据一般原理,对特殊情况作出的判断 用集合论的观点分析:若集合M中的所有元素都具有性质P,S是M的一个子集,那么S中所有元素也都具有性质P。 “三段论”可以表示为
大前题:M是P 小前提:S是M 结论:S是P。 (1)大前提……已知的一般原理(2)小前提……所研究的特殊情况
(3)结论……根据一般原理,对特殊情况作出的判断 MS大前题不正确推理形式 错误无限小数无限小数 ππ(1)大前提……已知的一般原理(2)小前提……所研究的特殊情况
(3)结论……根据一般原理,对特殊情况作出的判断 用三段论证明:函数f(x)=-x2+2x在(-∞,1]上是增函数。 大前提:增函数的定义
小前提:f(x)在(-∞,1]上满足定义
结论: f(x)在(-∞,1]上是增函数大前提:在区间(a,b)上如果f ’(x)>0,那么函
数y=f(x)在这个区间内单调递增
小前提:f(x)=-x2+2x在(-∞,1)上有f ‘(x)>0
结论: f(x)在(-∞,1]上是增函数(1)大前提……已知的一般原理(2)小前提……所研究的特殊情况
(3)结论……根据一般原理,对特殊情况作出的判断 归纳是由部分到整体、个体到一般的推理;类比推理是由特殊到特殊的推理由一般到特殊的推理不一定正确,有待于进一步证明大前提、小前提和推理形式都正确的前提下,得到的结论一定正确需要通过观察、实验等获取经验辨别它们的真伪,或将积累的知识加工、整理,使之条理化,系统化证明数学结论、建立数学体系的重要思维过程数学结论、证明思路等的发现 用三段论证明:若梯形的两个腰和一个底如果相等,它的对角线必平分另一底上的两个角。 证明:若三角形有两边相等,则三角形是等腰三角形………大前题
∵AD=DC …………………………………小前题
∴三角形ADC是等腰三角形………………结论等腰三角形的两底角相等………大前题
∵三角形ADC是等腰三角形,AD和DC是两腰………小前题
∴∠DAC= ∠DCA ………………结论两直线平行,内错角相等………大前题
∵∠DAC和∠ACB是AD∥BC的内错角………小前题
∴∠DAC=∠ACB ……… ………结论等于同一个量的两个量相等……………大前题
∴∠DCA和∠ACB都等于∠DAC ………小前题
∴∠DCA=∠ACB ………………………结论
∴AC平分∠DCB 同理, BD平分∠ABC 课堂小结:
1.俗话说,打鱼人识不完鱼,庄稼人识不完草。认识事物的任务十分艰巨,把握规律的道路分外漫长。我们不能事事去亲知,事事去实验。但是我们运用这种演绎方法,你就能以一知十,以近知远,以少知多。演绎推理还使人们产生新的创意或新的发现。
2.演绎方法是一种重要的认识工具,也是科学发现的有用方法。我们面前,一个无限广阔的世界正等待我们去认识,等待着我们去利用,去改造。(1)大前提……已知的一般原理(2)小前提……所研究的特殊情况
(3)结论……根据一般原理,对特殊情况作出的判断 结束
