人教版选修1-2 2.1.2演绎推理课件(21张)
文档属性
| 名称 | 人教版选修1-2 2.1.2演绎推理课件(21张) |

|
|
| 格式 | zip | ||
| 文件大小 | 561.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-22 17:04:26 | ||
图片预览






文档简介
课件21张PPT。温故知新:合情推理归纳推理2、归纳推理和类比推理区别?1、分类:1)归纳推理:特殊到一般2)类比推理:特殊到特殊3、合情推理的作用 提出猜想{类比推理学习目标:
1、什么是演绎推理?
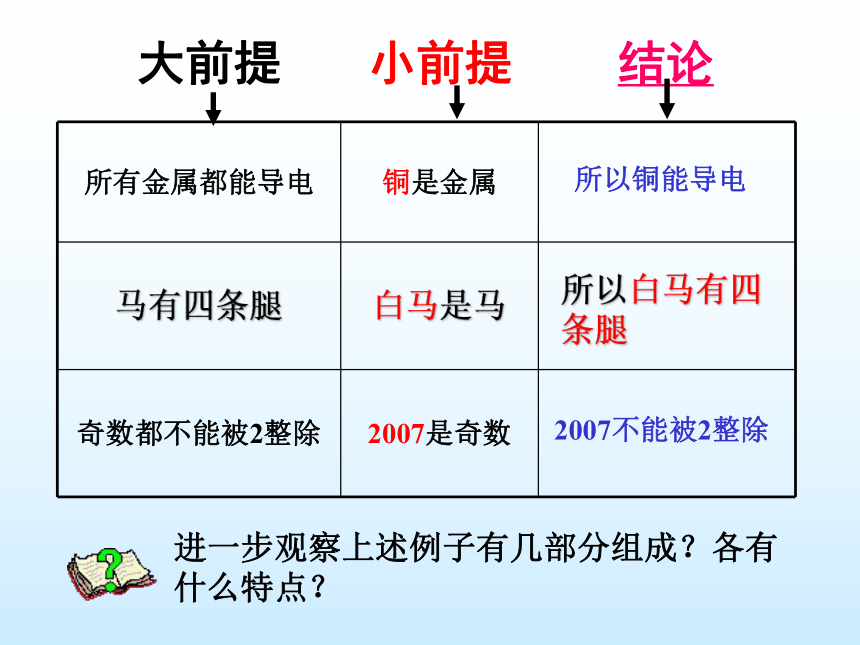
2、什么是三段论?三、新课填空并观察上述例子有什么特点? 1、演绎推理:由一般到特殊的推理。2007不能被2整除所以白马有四条腿所以铜能导电一般性原理特殊情况结论进一步观察上述例子有几部分组成?各有什么特点?大前提小前提结论2007不能被2整除所以白马有四条腿
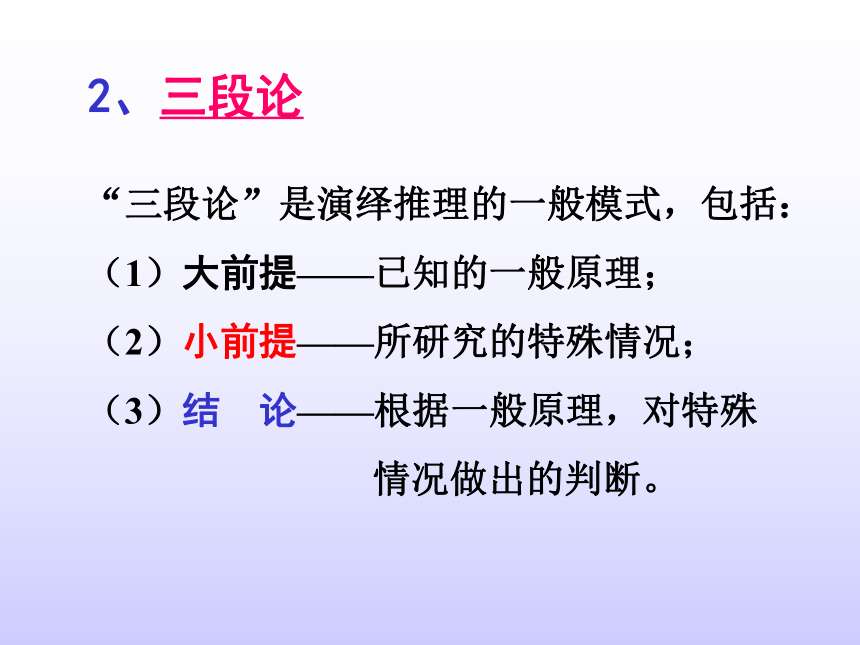
所以铜能导电“三段论”是演绎推理的一般模式,包括:
(1)大前提——已知的一般原理;
(2)小前提——所研究的特殊情况;
(3)结 论——根据一般原理,对特殊
情况做出的判断。
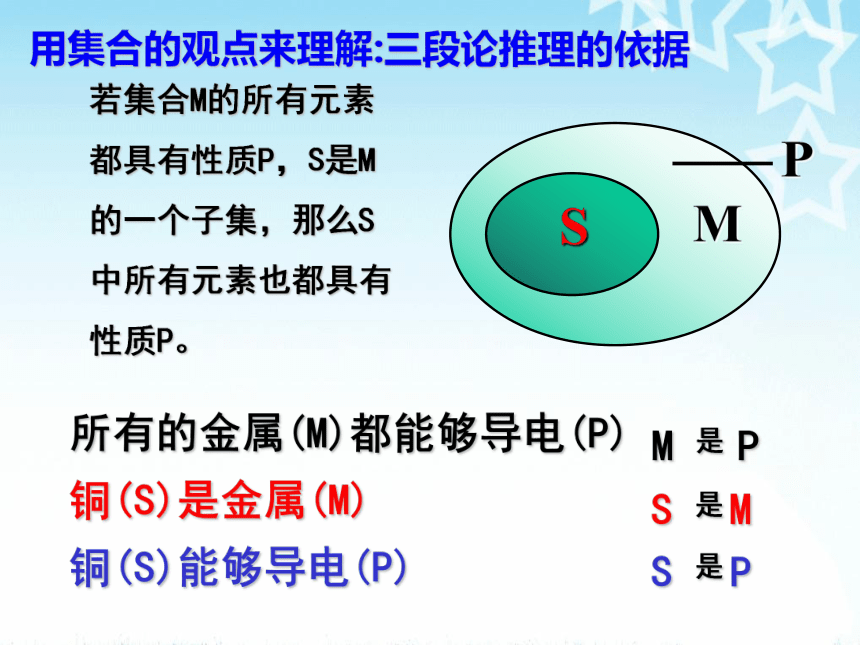
2、三段论若集合M的所有元素
都具有性质P,S是M
的一个子集,那么S
中所有元素也都具有
性质P。用集合的观点来理解:三段论推理的依据 例1:用三段论的形式写出下列演绎推理。
1.三角形内角和180°,等边三角形内角和是180°
大前提:三角形内角和180°
小前提:等边三角形是三角形
结论: 等边三角形内角和180°
小前提 : 是循环小数 是有理数。2、所有的循环小数都是有理数, 大前提:所有的循环小数都是有理数结论: 是有理数∵二次函数的图象是一条抛物线,练习:完成下面的推理过程
“二次函数y=x2 + x + 1的图象是 .”函数y = x2 + x + 1是二次函数,∴函数y = x2 + x + 1的图象是一条抛物线.大前提小前提结 论解:一条抛物线试将其恢复成完整的三段论.数学运用练习2: 分析下列推理是否正确,说明为什么?(1)自然数是整数,3是自然数,3是整数.推理形式错误小前提错误在演绎推理中,只要前提和推理形式是正确的,结论必定正确。大前提错误 想一想,做一做:推理形式正确,但推理结论错误,因为大前提错误。因为指数函数 是增函数(大前提)
而 是指数函数(小前提)
所以 是增函数(结论)
(1)上面的推理形式正确吗?
(2)推理的结论正确吗?为什么?演绎推理在前提和推理形式都正确时,得到的结论一定正确1、下面说法正确的有( )
(1)演绎推理是由一般到特殊的推理;
(2)演绎推理得到的结论一定是正确的;
(3)演绎推理一般模式是“三段论”形式;
(4)演绎推理的结论的正误与大前提、小前提和推理形式有关。
A、1个 B、2个 C、3个 D、4个C2、下列几种推理过程是演绎推理的是( )
A、5和 可以比较大小;
B、由平面三角形的性质,推测空间四面体的性质;
C、东升高中高二级有15个班,1班有51人,2班有53人,3班有52人,由此推测各班都超过50人;
D、预测股票走势图。A(2)因为直角三角形斜边上的中线等于斜边的一半, (1)因为有一个内角是直角的三角形是直角三角形,例3.如图;在锐角三角形ABC中,AD⊥BC, BE⊥AC,
D,E是垂足,求证:AB的中点M到D,E的距离相等在△ABC中,AD⊥BC,∠ADB=900,所以△ADB是直角三角形.同理△AEB是直角三角形.M是Rt△ADB斜边AB的中点,DM是斜边上的中线,所以 DM=EM.大前提小前提结论大前提小前提结论证明:注意:书写时,若大前提是显然的,可以省略,因为大前提 一般都是定理、公理、性质等
例2:证明函数f(x)=-x2+2x在(-∞,1)是增函数。大前提:增函数的定义;小前提结论例2:证明函数f(x)=-x2+2x在(-∞,1)是增函数。大前提:在某个区间(a,b)内若 ,那么函数y=f(x)在这个区间内单调递增;小前提结论 [例2] 如图,D,E,F分别是BC,CA,
AB上的点,∠BFD=∠A,DE∥BA,
求证:ED=AF,写出三段论形式的演绎
推理.[解答] ∵同位角相等,两条直线平行,……大前提
∠BFD与∠A是同位角,且∠BFD=∠A,…小前提
∴FD∥AE. …………………………………结论[研一题]∵两组对边分别平行的四边形是平行四边形,… 大前提
DE∥BA,且FD∥AE,…………………………… 小前提
∴四边形AFDE为平行四边形.………………… 结论
∵平行四边形的对边相等,…………………… 大前提
ED和AF为平行四边形AFDE的对边,……………小前提
∴ED=AF.………………………………………… 结论[通一类]2.如图所示,在空间四边形ABCD中,
点E,F分别是AB, AD的中点,
求证EF∥平面BCD. 证明:三角形的中位线平行于底边,…… 大前提
∵点E、F分别是AB、AD的中点,……… 小前提∴EF∥BD.……………………………… 结论
若平面外一条直线平行于平面内一条直线,则此直线与此平面平行,……………………… 大前提
∵EF?面BCD,BD?面BCD,EF∥BD…小前提
∴EF∥平面BCD.……………………………结论[研一题]
1、什么是演绎推理?
2、什么是三段论?三、新课填空并观察上述例子有什么特点? 1、演绎推理:由一般到特殊的推理。2007不能被2整除所以白马有四条腿所以铜能导电一般性原理特殊情况结论进一步观察上述例子有几部分组成?各有什么特点?大前提小前提结论2007不能被2整除所以白马有四条腿
所以铜能导电“三段论”是演绎推理的一般模式,包括:
(1)大前提——已知的一般原理;
(2)小前提——所研究的特殊情况;
(3)结 论——根据一般原理,对特殊
情况做出的判断。
2、三段论若集合M的所有元素
都具有性质P,S是M
的一个子集,那么S
中所有元素也都具有
性质P。用集合的观点来理解:三段论推理的依据 例1:用三段论的形式写出下列演绎推理。
1.三角形内角和180°,等边三角形内角和是180°
大前提:三角形内角和180°
小前提:等边三角形是三角形
结论: 等边三角形内角和180°
小前提 : 是循环小数 是有理数。2、所有的循环小数都是有理数, 大前提:所有的循环小数都是有理数结论: 是有理数∵二次函数的图象是一条抛物线,练习:完成下面的推理过程
“二次函数y=x2 + x + 1的图象是 .”函数y = x2 + x + 1是二次函数,∴函数y = x2 + x + 1的图象是一条抛物线.大前提小前提结 论解:一条抛物线试将其恢复成完整的三段论.数学运用练习2: 分析下列推理是否正确,说明为什么?(1)自然数是整数,3是自然数,3是整数.推理形式错误小前提错误在演绎推理中,只要前提和推理形式是正确的,结论必定正确。大前提错误 想一想,做一做:推理形式正确,但推理结论错误,因为大前提错误。因为指数函数 是增函数(大前提)
而 是指数函数(小前提)
所以 是增函数(结论)
(1)上面的推理形式正确吗?
(2)推理的结论正确吗?为什么?演绎推理在前提和推理形式都正确时,得到的结论一定正确1、下面说法正确的有( )
(1)演绎推理是由一般到特殊的推理;
(2)演绎推理得到的结论一定是正确的;
(3)演绎推理一般模式是“三段论”形式;
(4)演绎推理的结论的正误与大前提、小前提和推理形式有关。
A、1个 B、2个 C、3个 D、4个C2、下列几种推理过程是演绎推理的是( )
A、5和 可以比较大小;
B、由平面三角形的性质,推测空间四面体的性质;
C、东升高中高二级有15个班,1班有51人,2班有53人,3班有52人,由此推测各班都超过50人;
D、预测股票走势图。A(2)因为直角三角形斜边上的中线等于斜边的一半, (1)因为有一个内角是直角的三角形是直角三角形,例3.如图;在锐角三角形ABC中,AD⊥BC, BE⊥AC,
D,E是垂足,求证:AB的中点M到D,E的距离相等在△ABC中,AD⊥BC,∠ADB=900,所以△ADB是直角三角形.同理△AEB是直角三角形.M是Rt△ADB斜边AB的中点,DM是斜边上的中线,所以 DM=EM.大前提小前提结论大前提小前提结论证明:注意:书写时,若大前提是显然的,可以省略,因为大前提 一般都是定理、公理、性质等
例2:证明函数f(x)=-x2+2x在(-∞,1)是增函数。大前提:增函数的定义;小前提结论例2:证明函数f(x)=-x2+2x在(-∞,1)是增函数。大前提:在某个区间(a,b)内若 ,那么函数y=f(x)在这个区间内单调递增;小前提结论 [例2] 如图,D,E,F分别是BC,CA,
AB上的点,∠BFD=∠A,DE∥BA,
求证:ED=AF,写出三段论形式的演绎
推理.[解答] ∵同位角相等,两条直线平行,……大前提
∠BFD与∠A是同位角,且∠BFD=∠A,…小前提
∴FD∥AE. …………………………………结论[研一题]∵两组对边分别平行的四边形是平行四边形,… 大前提
DE∥BA,且FD∥AE,…………………………… 小前提
∴四边形AFDE为平行四边形.………………… 结论
∵平行四边形的对边相等,…………………… 大前提
ED和AF为平行四边形AFDE的对边,……………小前提
∴ED=AF.………………………………………… 结论[通一类]2.如图所示,在空间四边形ABCD中,
点E,F分别是AB, AD的中点,
求证EF∥平面BCD. 证明:三角形的中位线平行于底边,…… 大前提
∵点E、F分别是AB、AD的中点,……… 小前提∴EF∥BD.……………………………… 结论
若平面外一条直线平行于平面内一条直线,则此直线与此平面平行,……………………… 大前提
∵EF?面BCD,BD?面BCD,EF∥BD…小前提
∴EF∥平面BCD.……………………………结论[研一题]
