人教版选修1-2 2.2.1综合法和分析法课件(16张)
文档属性
| 名称 | 人教版选修1-2 2.2.1综合法和分析法课件(16张) |

|
|
| 格式 | zip | ||
| 文件大小 | 390.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-22 00:00:00 | ||
图片预览





文档简介
课件16张PPT。2.2.1 综合法和分析法 (1) 2.2直接证明与间接证明
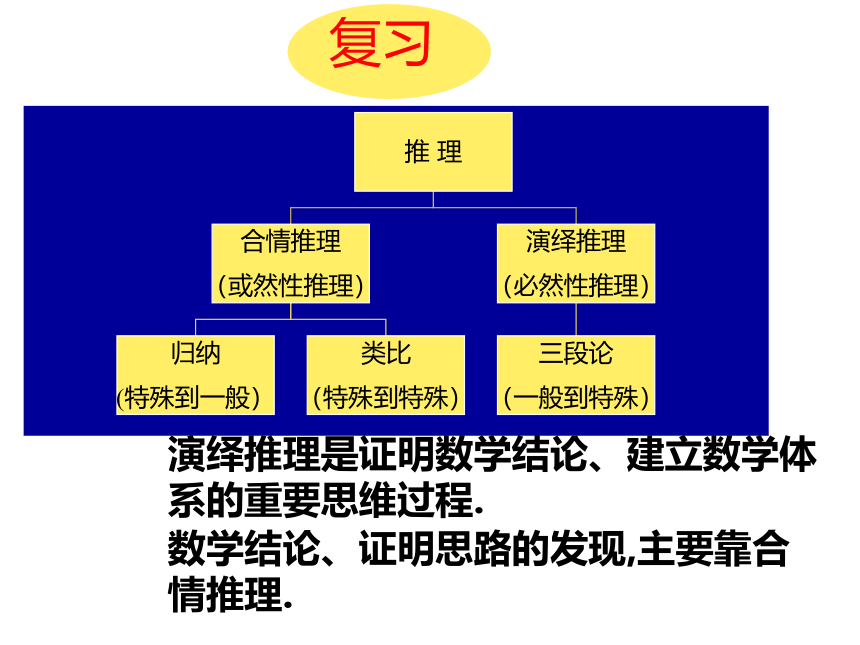
演绎推理是证明数学结论、建立数学体系的重要思维过程.数学结论、证明思路的发现,主要靠合情推理.复习
教学目标:1.知识与技能目标:
(1)理解综合法证明的概念;
(2)能熟练地运用综合法证明数学问题.
2.过程与方法目标:
通过实例引导学生分析综合法的思考过程与特点.
3.情感、态度与价值观
体会数学思维的严密性、抽象性、科学性.提问:合情推理得到的结论是不可靠的,需要证明。数学中证明的方法有哪些呢?引例:已知a>0,b>0,求证a(b2+c2)+b(c2+a2)≥4abc因为b2+c2 ≥2bc,a>0
所以a(b2+c2)≥2abc.又因为c2+b2 ≥2bc,b>0
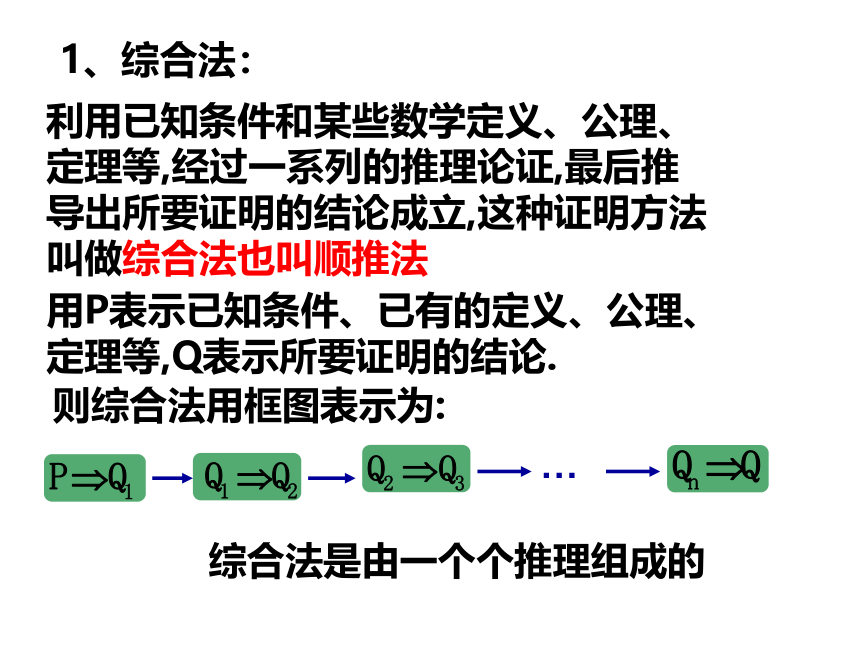
所以b(c2+a2)≥ 2abc.因此 a(b2+c2)+b(c2+a2)≥4abc.证明:在数学证明中,我们经常从已知条件和某些数学定义、定理、公理、性质等出发通过推理导出所要的结论。利用已知条件和某些数学定义、公理、定理等,经过一系列的推理论证,最后推导出所要证明的结论成立,这种证明方法叫做综合法也叫顺推法用P表示已知条件、已有的定义、公理、定理等,Q表示所要证明的结论.则综合法用框图表示为:…1、综合法:综合法是由一个个推理组成的直接证明1 概念
直接从原命题的条件逐步推得命题成立2 直接证明的一般形式:例1:如图,△ABC在平面α外,
求证:P,Q,R三点共线.分析:立体几何中证明三点共线或三线共点一般要用公理2。公理2的内容是什么?
此题要证明三点共线,需要说明这三点均在一个平面上,则这三点一定在交线上。
证明:(1)
(2)分析:由已知条件和结论我们联想到数量积定义和三解形的面积公式:由数量积定义和上公式结合结论探求证明思路证明:例3:在△ABC中,三个内角A、B、C对应的边分别为a、b、c,且A、B、C成等差数列,a、b、c成等比数列,求证△ABC为等边三角形.分析:把题中的文字语言转化为符号语言:A+C=2B⑴,b2 =ac⑵由(1)联想到内角各能得到什么?由(2)联想到三角形什么知识?余弦定理,二者联系起来能得到什么结论证明:由A,B,C成等差数列,有2B=A+C ① 由①②,得②③由啊,a,b,c成等比数列,有④由余弦定理及③,可得再由④,得因此,a=c从而有 A=C由②③⑤,得【巩固练习】利用已知条件和某些数学定义、公理、定理等,经过一系列的推理论证,最后推导出所要证明的结论成立,这种证明方法叫做综合法用P表示已知条件、已有的定义、公理、定理等,Q表示所要证明的结论.则综合法用框图表示为:…小结综合法的定义:
教学目标:1.知识与技能目标:
(1)理解综合法证明的概念;
(2)能熟练地运用综合法证明数学问题.
2.过程与方法目标:
通过实例引导学生分析综合法的思考过程与特点.
3.情感、态度与价值观
体会数学思维的严密性、抽象性、科学性.提问:合情推理得到的结论是不可靠的,需要证明。数学中证明的方法有哪些呢?引例:已知a>0,b>0,求证a(b2+c2)+b(c2+a2)≥4abc因为b2+c2 ≥2bc,a>0
所以a(b2+c2)≥2abc.又因为c2+b2 ≥2bc,b>0
所以b(c2+a2)≥ 2abc.因此 a(b2+c2)+b(c2+a2)≥4abc.证明:在数学证明中,我们经常从已知条件和某些数学定义、定理、公理、性质等出发通过推理导出所要的结论。利用已知条件和某些数学定义、公理、定理等,经过一系列的推理论证,最后推导出所要证明的结论成立,这种证明方法叫做综合法也叫顺推法用P表示已知条件、已有的定义、公理、定理等,Q表示所要证明的结论.则综合法用框图表示为:…1、综合法:综合法是由一个个推理组成的直接证明1 概念
直接从原命题的条件逐步推得命题成立2 直接证明的一般形式:例1:如图,△ABC在平面α外,
求证:P,Q,R三点共线.分析:立体几何中证明三点共线或三线共点一般要用公理2。公理2的内容是什么?
此题要证明三点共线,需要说明这三点均在一个平面上,则这三点一定在交线上。
证明:(1)
(2)分析:由已知条件和结论我们联想到数量积定义和三解形的面积公式:由数量积定义和上公式结合结论探求证明思路证明:例3:在△ABC中,三个内角A、B、C对应的边分别为a、b、c,且A、B、C成等差数列,a、b、c成等比数列,求证△ABC为等边三角形.分析:把题中的文字语言转化为符号语言:A+C=2B⑴,b2 =ac⑵由(1)联想到内角各能得到什么?由(2)联想到三角形什么知识?余弦定理,二者联系起来能得到什么结论证明:由A,B,C成等差数列,有2B=A+C ① 由①②,得②③由啊,a,b,c成等比数列,有④由余弦定理及③,可得再由④,得因此,a=c从而有 A=C由②③⑤,得【巩固练习】利用已知条件和某些数学定义、公理、定理等,经过一系列的推理论证,最后推导出所要证明的结论成立,这种证明方法叫做综合法用P表示已知条件、已有的定义、公理、定理等,Q表示所要证明的结论.则综合法用框图表示为:…小结综合法的定义:
