2.2两角和与差的正弦、余弦函数课件15张PPT
文档属性
| 名称 | 2.2两角和与差的正弦、余弦函数课件15张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 735.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-22 00:00:00 | ||
图片预览






文档简介
课件15张PPT。 北师大版高中数学必修4第三章三角恒等变形
§2 两角和与差的三角函数
2.1 两角差的余弦函数
2.2 两角和与差的正弦、余弦函数 (1课时)问题1:cos15°=? 问题2:cos15°=cos(45°- 30°)= ?cos(α-β) =? 1、已知OP为角?的终边,求终边与单位圆交点P的坐标?P(cos? ,sin? )2、两个向量的数量积:xy若,则温
故
知
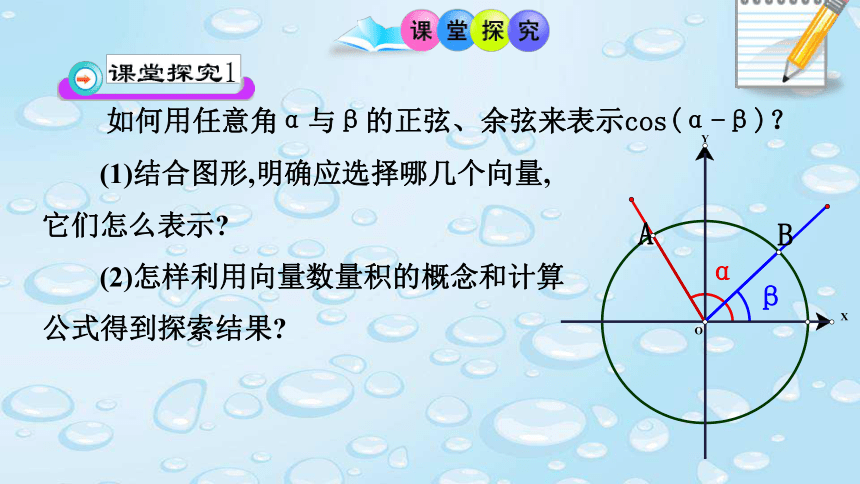
新!,其中θ∈[0,π] (1)结合图形,明确应选择哪几个向量,
它们怎么表示?
(2)怎样利用向量数量积的概念和计算
公式得到探索结果?如何用任意角α与β的正弦、余弦来表示cos(α-β)?分析:(2)不查表,求cos75°的值. ①这四个公式中的α、β都是任意角.
②两角和与差的余弦公式记忆“同名相乘,符号相异”.两角和与差的正弦公式记忆“异名相乘,符号相同”.
③正确识别公式的特征,掌握公式的正用和逆用,灵活运用公式进行恒等变形.
④两角和与差的三角函数公式是诱导公式的推广,诱导公式是它的特例.
注意: 练习题:
1.(1)两角和与差的正弦,余弦公式中角α,β是任意的.( )
(2)存在实数α,β,使cos(α+β)=cosα-cosβ成立.( )
(3)cos(α+β)=cosα-cosβ一定成立.( )
(4)cos(α-β)=cosαcosβ-sinαsinβ.( )
(5)sin(α+β)=sinα+sinβ一定不成立.( )答案:(1)√ (2)√ (3)× (4)×(5)× 所以cos(α-β)= cosβcosα+sinβsinα例2.总结:要求cos(α-β)应先求出α,β的正余弦,把下列各式化为一个角的三角函数形式令
例3.求f(x)=sinx+ cosx得最大值和周期.
1.本节课主要学习了:
2.首先要认识公式的结构特征,了解公式的推导过程.在解题过程中注意α、β所在的象限,也就是符号问题,学会灵活运用.谢谢!
§2 两角和与差的三角函数
2.1 两角差的余弦函数
2.2 两角和与差的正弦、余弦函数 (1课时)问题1:cos15°=? 问题2:cos15°=cos(45°- 30°)= ?cos(α-β) =? 1、已知OP为角?的终边,求终边与单位圆交点P的坐标?P(cos? ,sin? )2、两个向量的数量积:xy若,则温
故
知
新!,其中θ∈[0,π] (1)结合图形,明确应选择哪几个向量,
它们怎么表示?
(2)怎样利用向量数量积的概念和计算
公式得到探索结果?如何用任意角α与β的正弦、余弦来表示cos(α-β)?分析:(2)不查表,求cos75°的值. ①这四个公式中的α、β都是任意角.
②两角和与差的余弦公式记忆“同名相乘,符号相异”.两角和与差的正弦公式记忆“异名相乘,符号相同”.
③正确识别公式的特征,掌握公式的正用和逆用,灵活运用公式进行恒等变形.
④两角和与差的三角函数公式是诱导公式的推广,诱导公式是它的特例.
注意: 练习题:
1.(1)两角和与差的正弦,余弦公式中角α,β是任意的.( )
(2)存在实数α,β,使cos(α+β)=cosα-cosβ成立.( )
(3)cos(α+β)=cosα-cosβ一定成立.( )
(4)cos(α-β)=cosαcosβ-sinαsinβ.( )
(5)sin(α+β)=sinα+sinβ一定不成立.( )答案:(1)√ (2)√ (3)× (4)×(5)× 所以cos(α-β)= cosβcosα+sinβsinα例2.总结:要求cos(α-β)应先求出α,β的正余弦,把下列各式化为一个角的三角函数形式令
例3.求f(x)=sinx+ cosx得最大值和周期.
1.本节课主要学习了:
2.首先要认识公式的结构特征,了解公式的推导过程.在解题过程中注意α、β所在的象限,也就是符号问题,学会灵活运用.谢谢!
