必修4 第三章三角恒等变换 3.3二倍角的三角函数(一)课件26张PPT
文档属性
| 名称 | 必修4 第三章三角恒等变换 3.3二倍角的三角函数(一)课件26张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 861.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-22 21:26:58 | ||
图片预览







文档简介
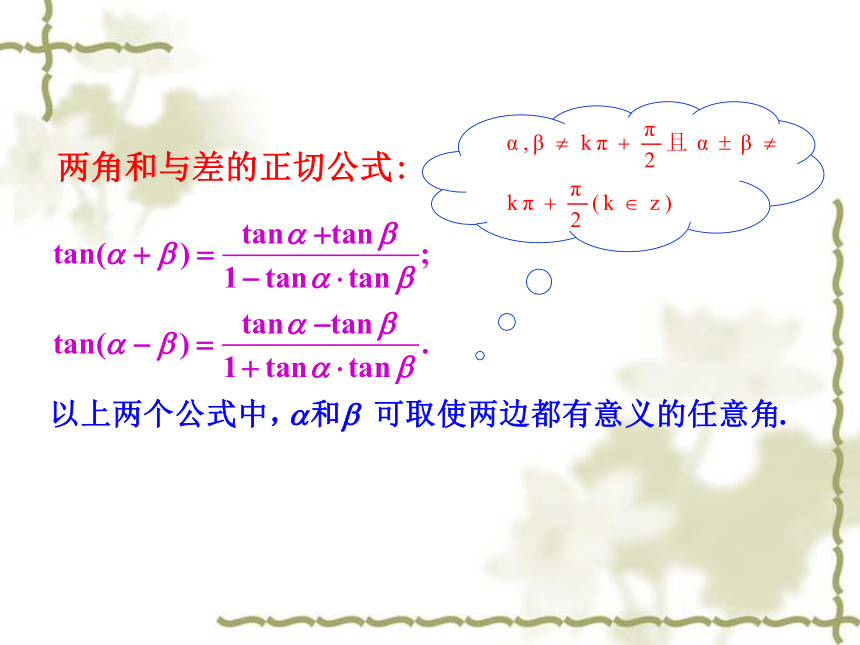
课件26张PPT。 二倍角的三角函数(一)北师大版必修四sin(a + b ) = sin a cos b cos a sin b .sin(a - b ) = sin a cos b cos a sin b ;cos(a + b ) = cos a cos b sin a sin b ; cos(a - b ) = cos a cos b sin a sin b ; -+-+以上公式中a和b可以取任意角.两角和与差的正切公式:1.能够导出二倍角的正弦、余弦、正切公式.(重点)
2.掌握二倍角的正弦、余弦、正切公式.(重点)
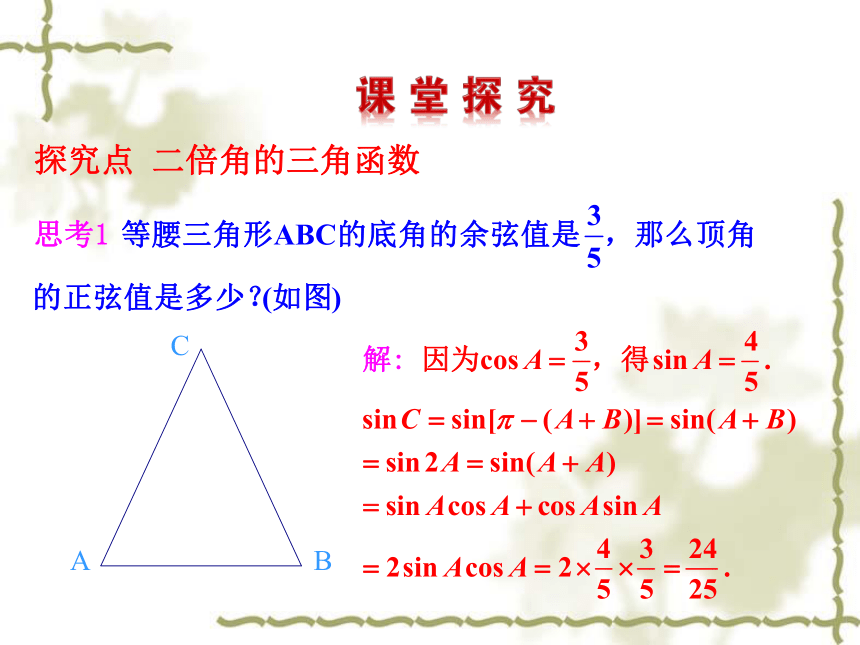
3.能灵活运用公式进行简单三角函数的化简、求值和证明.(难点)探究点 二倍角的三角函数 二倍角公式的推导:sin 2a = sin(a + a) = sin a cos a + cos a sin a = 2sin a cos a ;cos 2a = cos(a + a)= cos a cos a – sin a sin a= cos2a – sin2a ;tan 2a =tan(a + a)利用 sin2a + cos2a = 1,cos2a 还可变为cos 2a =cos2a – ( 1 - cos2a )= 2cos2a - 1;cos 2a = ( 1- sin2a ) - sin2a= 1 - 2sin2a .二倍角公式公式的特征与记忆:练一练填空:Sα+β
Cα+β提升总结:理解公式的推导方法关于公式的几个说明:1.公式 S2a 和 C2a 对任意角均成立,对于公式T2a3.注意公式的各种变化,如:4.注意公式的逆用:解例2 求下列各式的值: 解点评:直接运用公式将已知角转化为特殊角求值.1.二倍角公式的作用在于用单倍角的三角函数来表达二倍角的三角函数,它适用于二倍角与单倍角的三角函数之间的互化问题.
2.二倍角公式是从两角和的三角函数公式中,取两角相等时推导出来的,记忆时可联想相应角的公式.二倍角公式的作用:提升总结1.利用平方关系求三角函数值时,一定要注意角的取值范围.
2.求正切值时,常常采用商数关系,可以避免讨论符号问题.1.“切化弦”.
2.“异角化同角”.
3.注意逆用公式及公式的变形应用.
4.拼凑公式的形式,必要时利用诱导公式.提升总结:1.下列各式中值为 的是( )
A.2sin15°cos15° B.cos215°-sin215°
C.2sin215°-1 D.sin215°+cos215°
B4.化简、求值 5.若tan ? = 3,求sin2? ? cos2? 的值.1.方法上:学会怎样去发现数学规律,并体会从一般化归为特殊这一基本数学思想在探索中所起的作用.2.知识上:记住二倍角公式.3.公式变形:对一个人来说,所期望的不是别的,而仅仅是他能全力以赴和献身于一种美好事业.
——爱因斯坦
2.掌握二倍角的正弦、余弦、正切公式.(重点)
3.能灵活运用公式进行简单三角函数的化简、求值和证明.(难点)探究点 二倍角的三角函数 二倍角公式的推导:sin 2a = sin(a + a) = sin a cos a + cos a sin a = 2sin a cos a ;cos 2a = cos(a + a)= cos a cos a – sin a sin a= cos2a – sin2a ;tan 2a =tan(a + a)利用 sin2a + cos2a = 1,cos2a 还可变为cos 2a =cos2a – ( 1 - cos2a )= 2cos2a - 1;cos 2a = ( 1- sin2a ) - sin2a= 1 - 2sin2a .二倍角公式公式的特征与记忆:练一练填空:Sα+β
Cα+β提升总结:理解公式的推导方法关于公式的几个说明:1.公式 S2a 和 C2a 对任意角均成立,对于公式T2a3.注意公式的各种变化,如:4.注意公式的逆用:解例2 求下列各式的值: 解点评:直接运用公式将已知角转化为特殊角求值.1.二倍角公式的作用在于用单倍角的三角函数来表达二倍角的三角函数,它适用于二倍角与单倍角的三角函数之间的互化问题.
2.二倍角公式是从两角和的三角函数公式中,取两角相等时推导出来的,记忆时可联想相应角的公式.二倍角公式的作用:提升总结1.利用平方关系求三角函数值时,一定要注意角的取值范围.
2.求正切值时,常常采用商数关系,可以避免讨论符号问题.1.“切化弦”.
2.“异角化同角”.
3.注意逆用公式及公式的变形应用.
4.拼凑公式的形式,必要时利用诱导公式.提升总结:1.下列各式中值为 的是( )
A.2sin15°cos15° B.cos215°-sin215°
C.2sin215°-1 D.sin215°+cos215°
B4.化简、求值 5.若tan ? = 3,求sin2? ? cos2? 的值.1.方法上:学会怎样去发现数学规律,并体会从一般化归为特殊这一基本数学思想在探索中所起的作用.2.知识上:记住二倍角公式.3.公式变形:对一个人来说,所期望的不是别的,而仅仅是他能全力以赴和献身于一种美好事业.
——爱因斯坦
