必修4 第三章三角恒等变换 3.1同角三角函数的基本关系课件21张PPT
文档属性
| 名称 | 必修4 第三章三角恒等变换 3.1同角三角函数的基本关系课件21张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-22 21:33:56 | ||
图片预览







文档简介
课件21张PPT。科目:数学
年级:高一年级必修4
版本:北师大版
章节:第三章第一节
课程名称:同角三角函数的基本关系
资源类型:教学课件
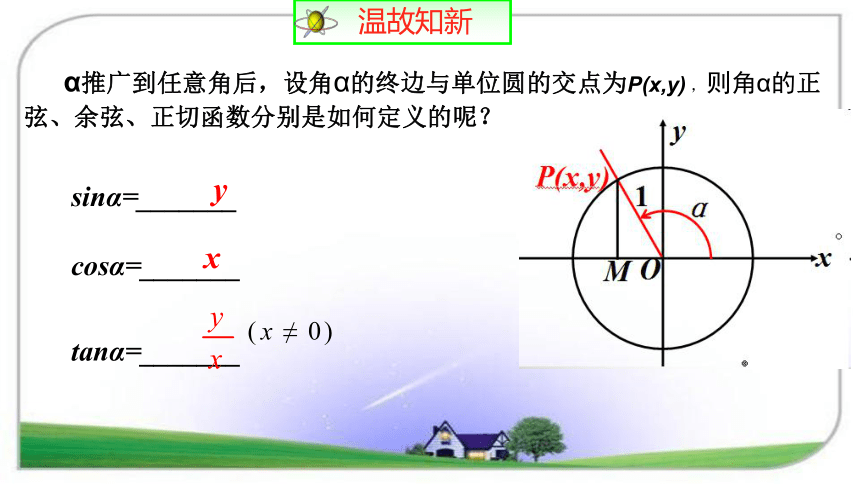
计算下列各式的值,你有什么发现?猜想:11 α推广到任意角后,设角α的终边与单位圆的交点为P(x,y) ,则角α的正弦、余弦、正切函数分别是如何定义的呢?sinα=_______
cosα=_______
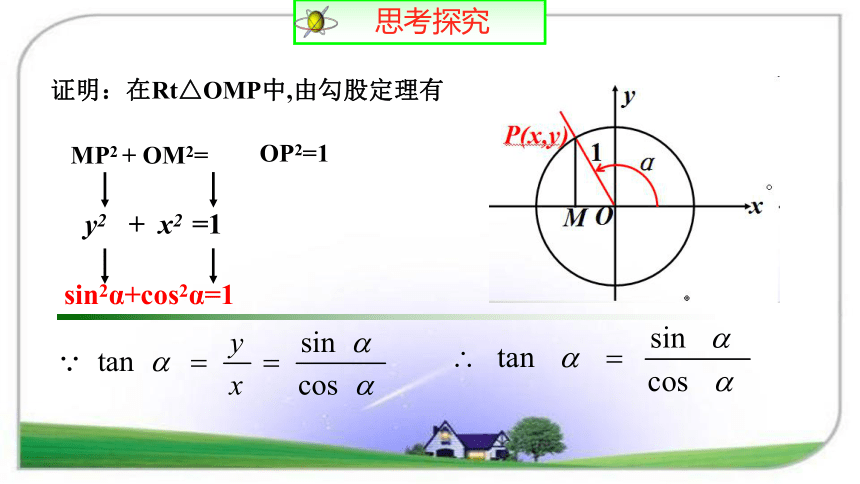
tanα=_______yx证明:在Rt△OMP中,由勾股定理有MP2 + OM2=OP2=1同角三角函数的基本关系同角三角函数基本关系式的应用1、一个三角函数值求出同角的其余两个三角函数值2、同角三角函数式的恒等变换3、化简三角函数式或证明三角恒等式.1
2
3
4
5
±sin2a + cos2a = 1同角三角函数的基本关系注: 公式成立的条件 ?同角?式子必须有意义 同角三角函数基本关系的变形1= 同角三角函数的基本关系揭示了同角之间的三角函数关系,其最基本的应用是“知一求二”,要注意这个角所在的象限,由此来决定所求的是一解还是两解,同时应体会方程思想的应用. ①关于sinα、cosα的齐次式,可以通过分子、分母同除以cos α或cos2α转化为关于tanα的式子后再求值.
②注意:(2)式中虽然不含分母,但是可以把分母看作1,通过1=sin2α+cos2α进行代换,再同除以cos2α,构造出关于tanα的代数式. 例3证法一:证法二:所以 交流总结证明一个三角恒等式的方法注意选择最优解
所以,原式成立 左边所以原式成立证法三:证明三角恒等式的常用方法有:
①直接法:从等式的一边开始直接化为等式的另一边.
②综合法:由一个已知成立的等式(如公式等)恒等变形得到所要证明的等式.
③中间量法:证明等式左右两式都等于同一个式子.
④比较法:设法证明:“左边-右边=0” .
(2)三种基本题型:
①三角函数值的计算问题:利用平方关系时,往往要开方,因此要先根据
角的所在象限确定符号,即将角所在象限进行分类讨论。
②化简题:一定要在有意义的前提下进行。
③证明问题。 本节课同学们有哪些学习体验与收获,学到了哪些数学知识与方法(3)数学思想方法:
①分类讨论;②方程(组)的思想;?化归思想 思考:已知sin θ+cos θ= ,θ∈(0,π),
求:(1) sin θcos θ ; (2) sin θ-cos θ 不渴望能够一跃千里,只希望每天能够前进一步。课本P117习题3—1 A组 1(2)(3)、2、3、6(1)(3)(5)谢谢
年级:高一年级必修4
版本:北师大版
章节:第三章第一节
课程名称:同角三角函数的基本关系
资源类型:教学课件
计算下列各式的值,你有什么发现?猜想:11 α推广到任意角后,设角α的终边与单位圆的交点为P(x,y) ,则角α的正弦、余弦、正切函数分别是如何定义的呢?sinα=_______
cosα=_______
tanα=_______yx证明:在Rt△OMP中,由勾股定理有MP2 + OM2=OP2=1同角三角函数的基本关系同角三角函数基本关系式的应用1、一个三角函数值求出同角的其余两个三角函数值2、同角三角函数式的恒等变换3、化简三角函数式或证明三角恒等式.1
2
3
4
5
±sin2a + cos2a = 1同角三角函数的基本关系注: 公式成立的条件 ?同角?式子必须有意义 同角三角函数基本关系的变形1= 同角三角函数的基本关系揭示了同角之间的三角函数关系,其最基本的应用是“知一求二”,要注意这个角所在的象限,由此来决定所求的是一解还是两解,同时应体会方程思想的应用. ①关于sinα、cosα的齐次式,可以通过分子、分母同除以cos α或cos2α转化为关于tanα的式子后再求值.
②注意:(2)式中虽然不含分母,但是可以把分母看作1,通过1=sin2α+cos2α进行代换,再同除以cos2α,构造出关于tanα的代数式. 例3证法一:证法二:所以 交流总结证明一个三角恒等式的方法注意选择最优解
所以,原式成立 左边所以原式成立证法三:证明三角恒等式的常用方法有:
①直接法:从等式的一边开始直接化为等式的另一边.
②综合法:由一个已知成立的等式(如公式等)恒等变形得到所要证明的等式.
③中间量法:证明等式左右两式都等于同一个式子.
④比较法:设法证明:“左边-右边=0” .
(2)三种基本题型:
①三角函数值的计算问题:利用平方关系时,往往要开方,因此要先根据
角的所在象限确定符号,即将角所在象限进行分类讨论。
②化简题:一定要在有意义的前提下进行。
③证明问题。 本节课同学们有哪些学习体验与收获,学到了哪些数学知识与方法(3)数学思想方法:
①分类讨论;②方程(组)的思想;?化归思想 思考:已知sin θ+cos θ= ,θ∈(0,π),
求:(1) sin θcos θ ; (2) sin θ-cos θ 不渴望能够一跃千里,只希望每天能够前进一步。课本P117习题3—1 A组 1(2)(3)、2、3、6(1)(3)(5)谢谢
