1.1 利用函数性质判定方程解的存在 课件19张PPT
文档属性
| 名称 | 1.1 利用函数性质判定方程解的存在 课件19张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 280.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-22 00:00:00 | ||
图片预览




文档简介
课件19张PPT。 4.1.1利用函数性质
判断
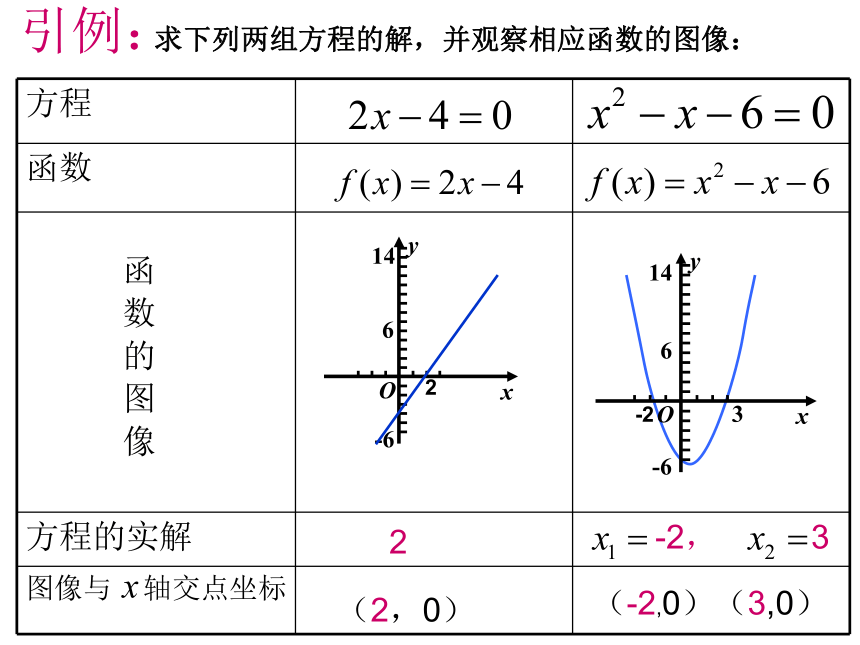
方程解的存在3x=x2 ?22(2,0)-2, 3(-2,0)(3,0)引例:求下列两组方程的解,并观察相应函数的图像:-2函 数 的 图 像思考推广:
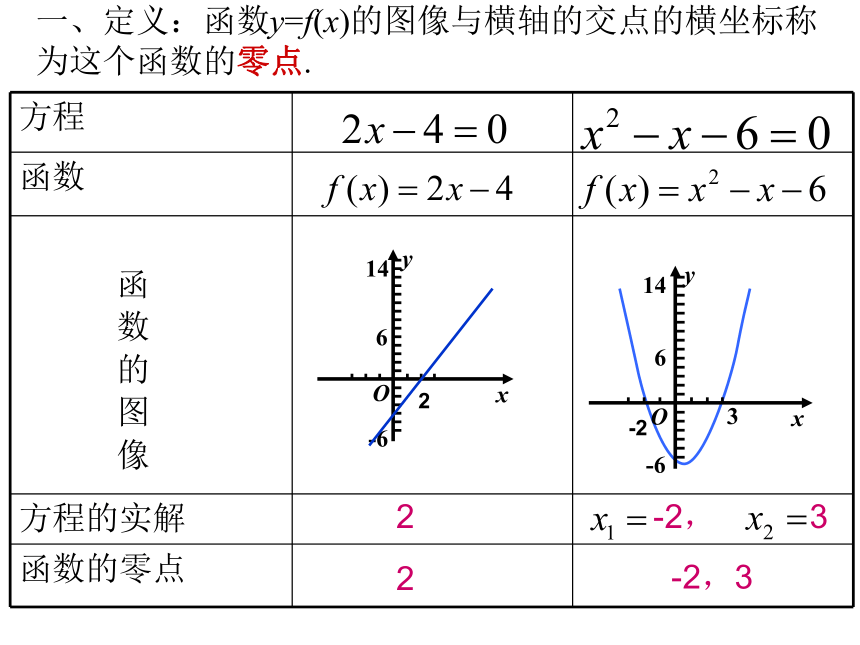
对于一切一元方程f(x)=0与其相应函数y=f(x): (1)若f(x)=0有实根c,即f(c)=0,则相应的函数y=f(x)图像必经过(c,0); (2)若方程f(x)=0没有实根,则相应的函数y=f(x)图像于x轴没有交点。222-2, 3-2,3-2函 数 的 图 像一、定义:函数y=f(x)的图像与横轴的交点的横坐标称为这个函数的零点.一、定义:函数y=f(x)的图像与横轴的交点的横坐标称为这个函数的零点.思考:如何找出函数的零点?
(1)方程f(x)=0的实数根;
(2)画出该函数图像;
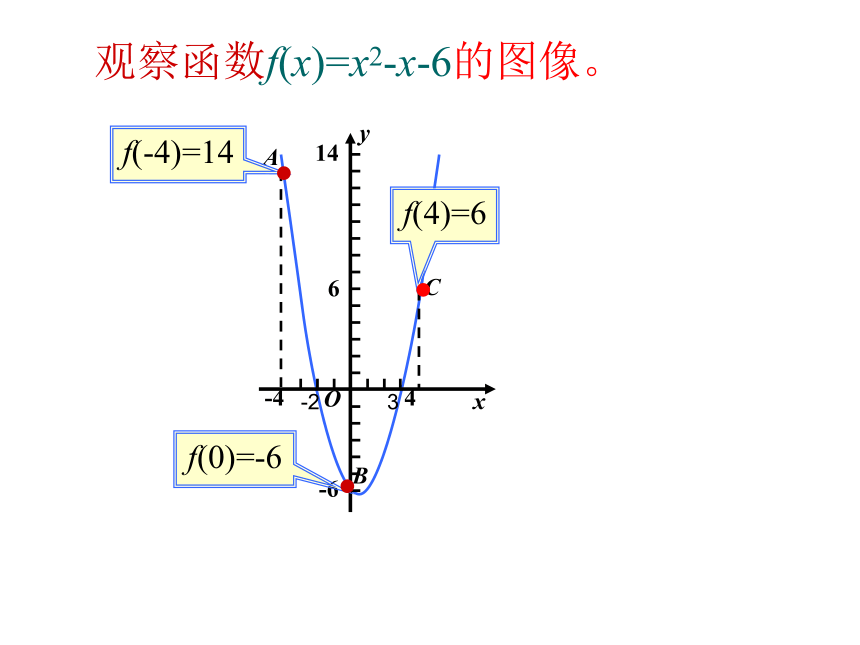
(3)在[a,b]上有没有零点呢?观察函数f(x)=x2-x-6的图像。f(0)=-6f(-4)=14f(4)=6B-23二:函数零点存在性的判定方法若函数y=f(x)满足:
①在闭区间[a,b]上的图像是连续曲线,
②并且在区间端点处的函数值符号相反(f(a)·f(b)<0)
则在区间(a,b)内,函数y=f(x)至少有一个零点,即相应的方程f(x)=0在(a,b)内至少有一个实数解。0.110abab例1 已知函数f(x)=3x-x2.问:方程f(x)=0在区间[-1,0]内有没有实数解?为什么?解 因为f(-1)=3-1-(-1)2=<0f(0)=30-(0)2=1>0函数f(x)=3x-x2的图像是连续曲线,所以f(x)在区间[-1,0]内有零点,即f(x)=0在区间[-1,0]内有实数解.1.观察下面的四个函数图像,指出在区间 (-∞,0)内,方程fi(x)=0(i=1,2,3,4)哪个有解?说明理由.堂上练习2.判定方程4x3+x-15=0在[1,2]内实数解的存在性,并说明理由.堂上练习解 考虑函数f(x)=4x3+x-15,有
f(1)=-10<0
f(2)=19>0
函数f(x)=4x3+x-15图像是连续曲线,
所以函数f(x)在区间[1,2]内有零点.
即方程4x3+x-15=0在区间[1,2]内有实数解.例2 判定方程(x-2)(x-5)=1有两个相异的实数解,且一个大于5,一个小于2.解:函数f(x)=(x-2)(x-5)-1
f(5)=(5-2)(5-5)-1=-1<0
f(2)=(2-2)(2-5)-1=-1<0
f(1)=(1-2)(1-5)-1=3>0
f(6)=(6-2)(6-5)-1=3>0
又f(x)的图像是连续曲线,
所以与横轴在(5,6)内有一交点,在(1,2)内也有一个交点.
方程(x-2)(x-5)=1有两个相异的实数解,且一个大于5,一个小于216例3:求f(x)=lnx+2x-6的零点个数。解:f(1)=ln1+2×1-6=-4<0
f(3)=ln3+2×3-6=ln3>0
又函数y=f(x)图象在定义域内是连续曲线,
所以函数y=f(x)在区间[1,3]有零点。
又函数y=f(x)图象在定义域内是单调增函数。
所以函数y=f(x)在区间[1,3]有一个零点。
若函数在区间【a,b】上,有零点,又单调,则函数在区间【a,b】上零点个数唯一。3.指出下列方程存在实数解,并给出一个实数解的存在区间:堂上练习1、学到什么知识;零点定义,利用函数性质判断方程
解的存在。 课堂小结:一:零点的定义:
函数y=f(x)的图像与横轴的交点的横坐标称为这个函数的零点.
二:函数零点存在性的判定方法
若函数y=f(x)满足:
①在闭区间[a,b]上的图像是连续曲线,
②并且在区间端点处的函数值符号相反(f(a)·f(b)<0)
则在区间(a,b)内,函数y=f(x)至少有一个零点,即相应的方程f(x)=0在(a,b)内至少有一个实数解。
课堂小结: 2、能解决什么问题;3、体会到什么样的探究数学问题的方法。1、学到什么知识;零点定义,利用函数性质判断方程
解的存在。对于不熟悉的方程判断解的存在。由特殊到一般补充练习1.若关于x的方程3x2-5x+a=0的一根大于-2小于0,另一根大于1小于3,求a的取值范围.解 设f(x)=3x2-5x+a,f(-2)>0
f(0)<0
f(1)<0
f(3)>0补充练习2.关于x的方程x2-2tx+t2-1=0的两根介于-2和4之间,求t的范围.解 设f(x)=x2-2tx+t2-1,则△>0
-2f(-2)>0
f(4)>0祝同学们学习快乐!谢谢大家!作业:若关于x的方程3x2-5x+a=0的一根大于-2小于0,另一根大于1小于3,求a的取值范围.
对于一切一元方程f(x)=0与其相应函数y=f(x): (1)若f(x)=0有实根c,即f(c)=0,则相应的函数y=f(x)图像必经过(c,0); (2)若方程f(x)=0没有实根,则相应的函数y=f(x)图像于x轴没有交点。222-2, 3-2,3-2函 数 的 图 像一、定义:函数y=f(x)的图像与横轴的交点的横坐标称为这个函数的零点.一、定义:函数y=f(x)的图像与横轴的交点的横坐标称为这个函数的零点.思考:如何找出函数的零点?
(1)方程f(x)=0的实数根;
(2)画出该函数图像;
(3)在[a,b]上有没有零点呢?观察函数f(x)=x2-x-6的图像。f(0)=-6f(-4)=14f(4)=6B-23二:函数零点存在性的判定方法若函数y=f(x)满足:
①在闭区间[a,b]上的图像是连续曲线,
②并且在区间端点处的函数值符号相反(f(a)·f(b)<0)
则在区间(a,b)内,函数y=f(x)至少有一个零点,即相应的方程f(x)=0在(a,b)内至少有一个实数解。0.110abab例1 已知函数f(x)=3x-x2.问:方程f(x)=0在区间[-1,0]内有没有实数解?为什么?解 因为f(-1)=3-1-(-1)2=<0f(0)=30-(0)2=1>0函数f(x)=3x-x2的图像是连续曲线,所以f(x)在区间[-1,0]内有零点,即f(x)=0在区间[-1,0]内有实数解.1.观察下面的四个函数图像,指出在区间 (-∞,0)内,方程fi(x)=0(i=1,2,3,4)哪个有解?说明理由.堂上练习2.判定方程4x3+x-15=0在[1,2]内实数解的存在性,并说明理由.堂上练习解 考虑函数f(x)=4x3+x-15,有
f(1)=-10<0
f(2)=19>0
函数f(x)=4x3+x-15图像是连续曲线,
所以函数f(x)在区间[1,2]内有零点.
即方程4x3+x-15=0在区间[1,2]内有实数解.例2 判定方程(x-2)(x-5)=1有两个相异的实数解,且一个大于5,一个小于2.解:函数f(x)=(x-2)(x-5)-1
f(5)=(5-2)(5-5)-1=-1<0
f(2)=(2-2)(2-5)-1=-1<0
f(1)=(1-2)(1-5)-1=3>0
f(6)=(6-2)(6-5)-1=3>0
又f(x)的图像是连续曲线,
所以与横轴在(5,6)内有一交点,在(1,2)内也有一个交点.
方程(x-2)(x-5)=1有两个相异的实数解,且一个大于5,一个小于216例3:求f(x)=lnx+2x-6的零点个数。解:f(1)=ln1+2×1-6=-4<0
f(3)=ln3+2×3-6=ln3>0
又函数y=f(x)图象在定义域内是连续曲线,
所以函数y=f(x)在区间[1,3]有零点。
又函数y=f(x)图象在定义域内是单调增函数。
所以函数y=f(x)在区间[1,3]有一个零点。
若函数在区间【a,b】上,有零点,又单调,则函数在区间【a,b】上零点个数唯一。3.指出下列方程存在实数解,并给出一个实数解的存在区间:堂上练习1、学到什么知识;零点定义,利用函数性质判断方程
解的存在。 课堂小结:一:零点的定义:
函数y=f(x)的图像与横轴的交点的横坐标称为这个函数的零点.
二:函数零点存在性的判定方法
若函数y=f(x)满足:
①在闭区间[a,b]上的图像是连续曲线,
②并且在区间端点处的函数值符号相反(f(a)·f(b)<0)
则在区间(a,b)内,函数y=f(x)至少有一个零点,即相应的方程f(x)=0在(a,b)内至少有一个实数解。
课堂小结: 2、能解决什么问题;3、体会到什么样的探究数学问题的方法。1、学到什么知识;零点定义,利用函数性质判断方程
解的存在。对于不熟悉的方程判断解的存在。由特殊到一般补充练习1.若关于x的方程3x2-5x+a=0的一根大于-2小于0,另一根大于1小于3,求a的取值范围.解 设f(x)=3x2-5x+a,f(-2)>0
f(0)<0
f(1)<0
f(3)>0补充练习2.关于x的方程x2-2tx+t2-1=0的两根介于-2和4之间,求t的范围.解 设f(x)=x2-2tx+t2-1,则△>0
-2
f(4)>0祝同学们学习快乐!谢谢大家!作业:若关于x的方程3x2-5x+a=0的一根大于-2小于0,另一根大于1小于3,求a的取值范围.
